Американські математики виявили раніше невідоме майно прем'єрних номерів

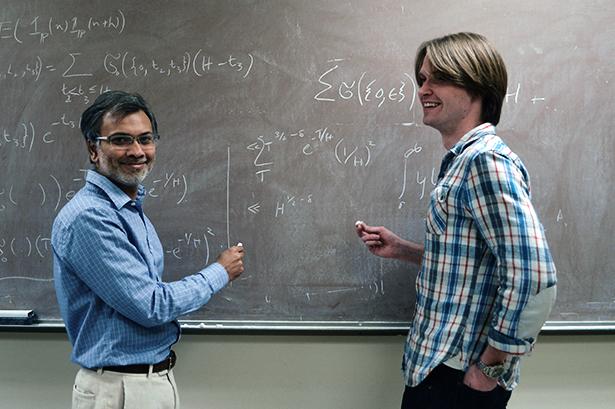
Два Станфордського університету математики, Каннан Soundararajan і Роберт Лемке Олівець (написаний вище) виявили раніше невідоме майно першоджерело номерів. Виявилося, що шанси на перше число, що закінчується в 9-му році, а також закінчуючи числом в 1 - 65% більше, ніж шанси, які слідують за номером, що закінчується в 9. Це припущення було чисельно перевірено комп’ютерними методами для мільярдів відомих прем’єрних чисел.

За словами Кена Оно, математика в Університеті Emory в Атланті, це припущення істотно суперечить очікуванням більшості математиків. По-перше, вважалося, що першоджерело число в їх масі досить випадково. Більшість учасників погоджуються на припущення, що шанси на те, що на кінець одного з можливих прем'єрних чисел (1, 3, 7, 9) є приблизно рівні для всіх таких чисел.

Андрій Гранвіль, Університет Монреаль, сказав: Ми вивчаємо першокласні номери, і ніхто не помітив. Це божевільний. Я не можу вірити, хто може думати про це. Це виглядає дуже дивно. й

Soundarajan сказав, що він надихнув ідею тестування «поваги» у світі прем’єрних номерів лекцією японського математика Tadashi Tokieda. Він дав приклад від теорії ймовірності. Якщо Аліса кидає монети, поки вона отримує хвіст поруч з орелою, і Боб доки вона отримує два хвости в рядку, Аліса буде потрібно в середньому чотири, тоді як Боб буде потрібно шість. При цьому ймовірність втрати орел і хвости однакова.

Так як Soundarajan був стурбований першими номерами, він перетворився на них у пошуках раніше невідомих розподілів. Він знайшов, що якщо ми писали в потрійну систему, в якій близько половини прем'єрних чисел закінчилися в 1 і половину в 2, то для прем'єрних чисел менше 1000, число закінчується в 1 буде двічі, як ймовірно, слідувати за номером, що закінчується в 2, ніж знову на 1.

Він поділився цікавим відкриттям з іншим вченим, Лемке Оливець, який, засвідчений цим фактом, написав програму, яка випробувала розподіл номерів на перших 400 мільярдів прем'єрних числах. Результати підтвердили припущення, що, як Олівець кладе його, першоджерело число «відкликання». Випробувано припущення як для десяткових, так і деяких інших систем.

Не відомо, чи є ця властивість окремого явища, або пов'язана з більш глибокими властивостями першоджерело, які ще не були виявлені. Як сказав Гранвіль, «Я дивлю, що ще ми можемо пропустити в першорядних числах. й

Джерело: habrahabr.ru/post/279337/