matemáticos estadounidenses descubrieron una propiedad hasta ahora desconocido de números primos

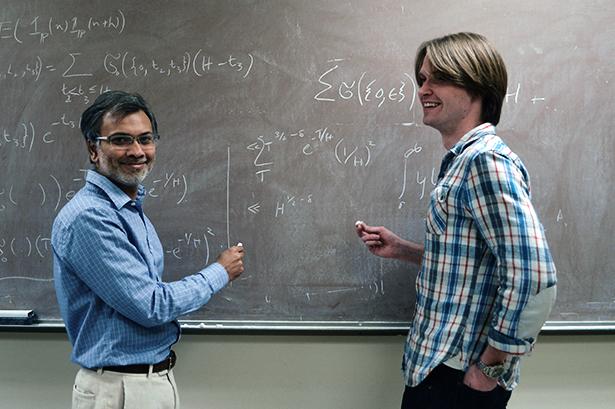
Dos matemáticas de la Universidad de Stanford, Kannan Soundaradzhan [Kannan Soundararajan] y Robert Lemke, Oliver [Robert Oliver Lemke] (en la foto) han descubierto una propiedad hasta ahora desconocido de números primos. Se encontró que las posibilidades de que para un número primo que termina en 9 seguirán los números que terminan en 1, 65% mayores que las posibilidades de que se seguirá para el número, de nuevo termina en 9. Esta hipótesis fue probada por el equipo numéricamente métodos para los miles de millones de números primos conocidos.
De acuerdo con Ken Ono, matemático de la Universidad de Emory en Atlanta, esta suposición es esencialmente contrario a las expectativas de la mayoría de los matemáticos. Anteriormente se pensaba que los números primos en la masa se comportan casi por accidente. La mayoría de los teóricos han convergido en el supuesto de que las posibilidades de tener al final de uno de los posibles números a los números primos (1, 3, 7, 9) son aproximadamente iguales para todos esos números.
Andrew Granville [Andrew Granville] de la Universidad de Montreal, dijo que "estamos inmersos en el estudio de los números primos durante mucho tiempo, y nadie se había dado cuenta. Esto es una locura para algunos. No puedo creer que alguien era capaz de pensar en esto. Parece muy extraño. »Blog Soundaradzhan dijo que llevó a la idea de cheques "al azar" en el mundo de los números primos conferencia Tadashi japonesa matemático Tokieda [Tadashi Tokieda]. En él dio el ejemplo de la teoría de la probabilidad. Si Alice está lanzando una moneda hasta que hasta que recibe colas siguiendo el águila, y Bob - hasta entonces, hasta que recibe dos caras de una vez, a continuación, Alice, en promedio toman cuatro lanzamiento de la moneda, mientras que Bob - seis. En este caso la probabilidad de caras y cruces es el mismo.
Desde Soundaradzhan estudió los números primos, se dirigió a ellos en la búsqueda de las distribuciones hasta ahora desconocidas. Él encontró que si escribimos los números primos en el sistema ternario en el que aproximadamente la mitad de los números primos termina con el número 1, y la otra mitad - el número 2, a continuación, los números primos menos de 1000 para un número que termina en el número 1, dos veces más probabilidades de ser siga los números que terminan en 2, que de nuevo el 1.
Compartió interesante descubrimiento con otros científicos, Oliver Lemke, que, golpean este hecho, escribió un programa para comprobar cómo van las cosas con la distribución de los números en el los primeros $ 400 millones de dólares de los números primos. Los resultados confirmaron la hipótesis - en palabras de Oliver, los números primos "odian la repetición." La suposición ha sido probado y notación decimal, y para algunos otros sistemas numéricos.
Hasta el momento no se sabe si se trata de la propiedad de algún fenómeno individual o asociada con propiedades más profundas de los números primos aún no está abierto. Como dijo Granville, "Me pregunto ¿qué otra cosa que no pudimos ver en los números primos?".
Fuente: habrahabr.ru/post/279337/