American mathematicians discovered a previously unknown property of prime numbers

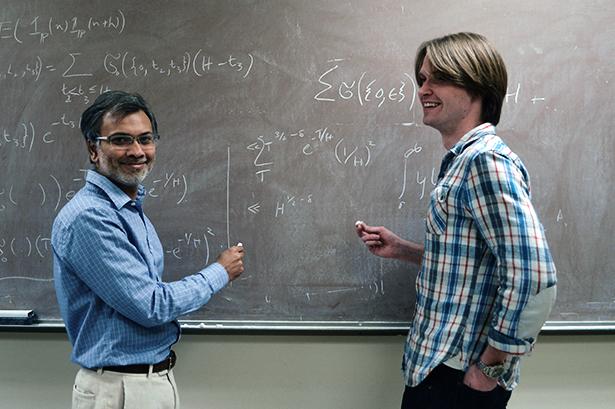
Two mathematics from Stanford University, Kannan Soundaradzhan [Kannan Soundararajan] and Robert Lemke, Oliver [Robert Lemke Oliver] (pictured above) have discovered a previously unknown property of prime numbers. It was found that the chances of that for a prime number ending in 9 will follow the numbers ending in 1, 65% greater than the chances that it will follow for the number, again ending in 9. This hypothesis was tested by computer numerically methods for the billions of known primes.

According to Ken Ono, mathematician at Emory University in Atlanta, this assumption is essentially contrary to the expectations of the majority of mathematicians. Previously it was thought that the prime numbers in the mass behave quite by accident. Most theorists have converged on the assumption that the chances of having at the end of one of the possible numbers to prime numbers (1, 3, 7, 9) are approximately equal for all such numbers.

Andrew Granville [Andrew Granville] from the University of Montreal, said that "we are engaged in the study of prime numbers for a long time, and no one had not noticed. This is madness for some. I can not believe that someone was able to think of this. It looks very strange. »

Soundaradzhan said that it prompted the idea of ​​"random" checks in the world of prime numbers lecture Tadashi Japanese mathematician Tokieda [Tadashi Tokieda]. In it he gave the example of the theory of probability. If Alice is throwing a coin until until it receives tails following the eagle, and Bob - until then, until it receives two heads in a row, then Alice, on average take four coin toss, while Bob - six. In this case the probability of heads and tails is the same.

Since Soundaradzhan studied prime numbers, he addressed them in the search for hitherto unknown distributions. He found that if we write the primes in the ternary system in which about half of the prime numbers ends with the number 1, and the other half - the number 2, then the prime numbers less than 1000 for a number ending in the number 1, two times more likely to be follow the numbers ending in 2, than again on 1.

He shared interesting discovery with other scientists, Oliver Lemke, who, hit this fact, wrote a program to check how things are going with the distribution of the numbers on the first $ 400 billion of prime numbers. The results confirmed the assumption - in the words of Oliver, prime numbers "hate repetition." The assumption has been tested and decimal notation, and for some other number systems.

So far it is unknown whether it is the property of some individual phenomenon or associated with deeper properties of prime numbers is not open yet. As Granville said, "I wonder what else we could not see in prime numbers?".

Source: habrahabr.ru/post/279337/