My daughter has a limping mathematics, found an example to reveal to her the beauty of the subject Bashny.Net

“A correct view of mathematics reveals not only truth, but impeccable beauty.” – Bertrand Russell The beauty of mathematics is not just a figure of speech, but a scientific fact. To prove this, scientists from the University of Edinburgh assessed brain activity in mathematicians looking at elegant mathematical formulas. It turned out that the brain perceives them in the same way as beautiful paintings, music or poems.



The sum of numbers from 1 to 100 German mathematician, physicist and astronomer Karl Gauss from childhood had extraordinary abilities. During his time at school, he surprised his teachers.



So, one day, Karl's teacher decided to keep the children busy for a long time. He asked them to find the sum of all the natural numbers from 1 to 100. To the surprise of the teacher, Gauss coped with the task very quickly, finding a beautiful pattern, which is still used by us in oral account.

1 + 2 + 3 + 4 + 5 + 6 + ... + 48 + 49 + 50 + 51 + 52 + 53 + ... + 95 + 96 + 97 + 98 + 99 + 100

Look carefully and try to guess what the young genius could see. The boy grouped the numbers as follows.

(1 + 100) + (2 + 99) + (3 + 98) + (4 + 97) + ... + (48 + 53) + (49 + 52) + (50 + 51)

50 x 101 = 5050

In the end, he got 50 pairs of numbers, the sum of each of which is easy to see is 101. So the sum of the natural numbers from 1 to 100 is 5050. A simple and elegant solution!



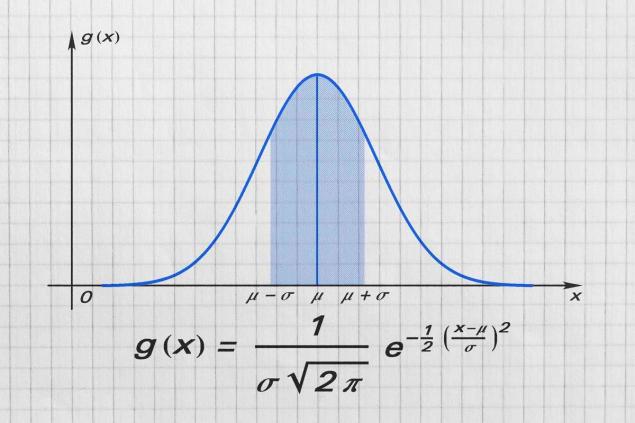
Gauss later developed a curve named after him, which clearly shows the probability distribution. It is directly related not only to academic science, but also to our everyday life. Let's put 40 people in your class. If you make a graph, where on the x-axis there will be growth in centimeters, and on the y-axis there will be the number of students with a particular height, then it will take the form of a Gauss curve (the so-called “bell”). The more people there are, the more accurate and symmetrical the graph will be. It's simple!

Multiplication of numbers consisting of units by themselves Multiply the same number of units and as a result, we get a set of numbers that should be looked at more closely. For example, 1111 x 1111 = 1234.321



As you can see, the result consists of two mirror halves, and the symmetry point in it corresponds to the number of units. Knowing this, 111111111 by 111111111 can be easily multiplied without a calculator and counting into a column. Just write the numbers from 1 to 9 and then the same sequence in reverse order. Mathematics is interesting and beautiful!

Multiply the number 123456789 by 9 and another digit If you multiply the number of nine consecutive digits by 9, and then another digit from 1 to 9, you get an amazing result.



In each case, it will be a set of nine digits corresponding to the last multiplier and zero in the penultimate place.

Multiply the numbers by 8 or 9 and add another digit As seen in the first photo, multiplying the numbers 1, 12, 123, 1234 and so on by 8 can achieve very remarkable results. Perhaps because 8 is the sign of infinity. But the nine is not a shiny shin. And she has a few surprises in store.



Multiply the same numbers by 9 and add 1 to 9. The result is a set of units and zero. At the same time, the number of units will always correspond to the number with the + sign. For example, 12345 x 9 + 5 = 111110 (+5 and five zero units in response).

These are just a few examples of the beauty and symmetry of mathematics. There is nothing supernatural in them - the usual mathematical actions, with the help of which you can get no less beautiful numbers from beautiful sets of numbers.