Mi hija tiene una matemática cojeante, encontró un ejemplo para revelar a ella la belleza del tema

“Una visión correcta de las matemáticas revela no sólo la verdad, sino la belleza impecable.” – Bertrand Russell La belleza de las matemáticas no es sólo una figura del discurso, sino un hecho científico. Para probar esto, científicos de la Universidad de Edimburgo evaluaron la actividad cerebral en matemáticos mirando fórmulas matemáticas elegantes. Resulta que el cerebro los percibe de la misma manera que hermosas pinturas, música o poemas.



La suma de números de 1 a 100 matemáticos alemanes, físicos y astrónomos Karl Gauss de la infancia tenía habilidades extraordinarias. Durante su tiempo en la escuela, sorprendió a sus maestros.



Un día, el profesor de Karl decidió mantener a los niños ocupados durante mucho tiempo. Les pidió que encontraran la suma de todos los números naturales de 1 a 100. Para la sorpresa del maestro, Gauss copió con la tarea muy rápidamente, encontrando un patrón hermoso, que todavía es utilizado por nosotros en cuenta oral.

1 + 2 + 3 + 4 + 5 + 6 + ... + 48 + 49 + 50 + 51 + 53 + ... + 95 + 96 + 97 + 99 + 100

Mira cuidadosamente y trata de adivinar lo que el joven genio podía ver. El niño agrupaba los números como sigue.

(1 + 100) + (2 + 99) + (3 + 98) + (4 + 97) + ... + (48 + 53) + (49 + 52) + (50 + 51)

50 x 101 = 5050

Al final, tiene 50 pares de números, la suma de cada uno de los cuales es fácil de ver es 101. Así que la suma de los números naturales de 1 a 100 es 5050. ¡Una solución sencilla y elegante!



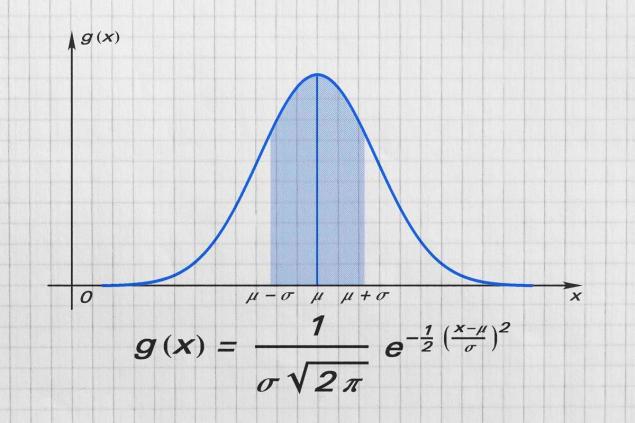
Gauss más tarde desarrolló una curva llamada después de él, que muestra claramente la distribución de probabilidad. Está directamente relacionada no sólo con la ciencia académica, sino también con nuestra vida cotidiana. Pongamos a 40 personas en su clase. Si usted hace un gráfico, donde en el eje x habrá crecimiento en centímetros, y en el eje y habrá el número de estudiantes con una altura particular, entonces tomará la forma de una curva de Gauss (la llamada “belle”). Cuanto más gente haya, más preciso y simétrico será el gráfico. ¡Es simple!

Multiplicación de números consistentes en unidades por sí mismos Multiply el mismo número de unidades y como resultado, obtenemos un conjunto de números que deben ser mirados más de cerca. Por ejemplo, 1111 x 1111 = 1234.321



Como se puede ver, el resultado consta de dos mitades de espejo, y el punto de simetría en él corresponde al número de unidades. Conociendo esto, 111111111 por 111111111 se puede multiplicar fácilmente sin una calculadora y contando en una columna. Simplemente escriba los números de 1 a 9 y luego la misma secuencia en orden inverso. ¡Matemática es interesante y hermosa!

Multiplicar el número 123456789 por 9 y otro dígito Si multiplicas el número de nueve dígitos consecutivos por 9, y luego otro dígito de 1 a 9, obtienes un resultado increíble.



En cada caso, será un conjunto de nueve dígitos correspondientes al último multiplicador y cero en el penúltimo lugar.

Multiplicar los números por 8 o 9 y añadir otro dígito Como se ve en la primera foto, multiplicar los números 1, 12, 123, 1234 y así sucesivamente por 8 puede lograr resultados muy notables. Quizás porque 8 es la señal del infinito. Pero el nueve no es una brillante cama. Y tiene algunas sorpresas en la tienda.

5418857

Multiplicar los mismos números por 9 y añadir 1 a 9. El resultado es un conjunto de unidades y cero. Al mismo tiempo, el número de unidades siempre corresponderá al número con el signo +. Por ejemplo, 12345 x 9 + 5 = 111110 (+5 y cinco unidades cero en respuesta).

Estos son sólo algunos ejemplos de la belleza y la simetría de las matemáticas. No hay nada sobrenatural en ellos - las acciones matemáticas habituales, con la ayuda de la que usted puede conseguir no menos números hermosos de hermosos conjuntos de números.