187
Моя дочка має limping математику, знайдений приклад для виявлення її краси предмета
«Правильний вигляд математики розкриває не тільки правду, але бездоганна краса». – Бертранда Руссел Краса математики – це не просто фігура мови, але і науковий факт. Довести це, вчені з Університету Едінбург оцінили роботу мозку в математиках, які шукають елегантні математичні формули. Виявилося, що мозок сприймає їх таким же чином, як красиві картини, музика або вірші.
 р.
р.
Сума чисел від 1 до 100 німецького математика, фізика та астронома Карла Гауса з дитинства мала надзвичайні здібності. Під час своєї школи він здивував своїх вчителів.

Так, один день, вчитель Карла вирішив довго тримати дітей. Він просить їх знайти суму всіх природних чисел від 1 до 100. Щоб здивувати вчителя, гаус справляється з завданням дуже швидко, знайдіть гарний візерунок, який ще використовується нами в усному обліковому записі.
1 + 2 + 3 + 4 + 5 + 6 + + 48 + 49 + 50 + 51 + 53 + 96 + 96 + 97 + 98 + 99 + 100
Дивись уважно і намагайтеся вгадати, що може бачити молодий геній. Хлопці згрупували цифри наступним чином.
1 + 100) + (2 + 99) + (3 + 98) + (4 + 97) + + (48 + 53) + (49 + 52) + (50 + 51)
50 кс 101 = 5050
В кінці він отримав 50 пар чисел, сума кожного з яких легко побачити - 101. Так сума натуральних чисел від 1 до 100 5050. Простий і елегантний рішення!
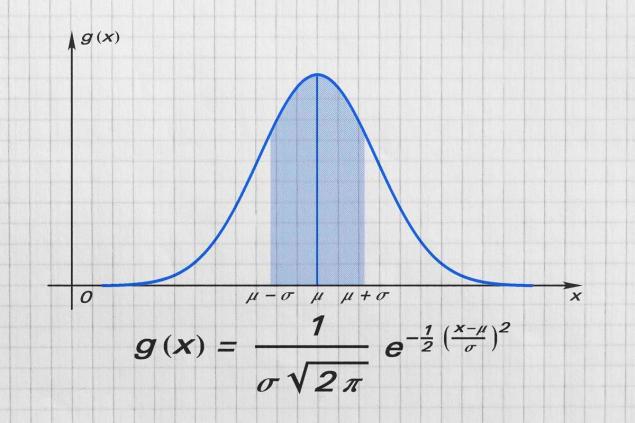
Після того, як він розвив криву, яка чітко показує розподіл ймовірностей. Це безпосередньо пов’язано не тільки з академічною наукою, але й нашим повсякденним життям. Поставимо 40 людей у своєму класі. Якщо ви зробите графік, де на осі x буде рости в сантиметрах, а на вісь буде кількість студентів з певною висотою, то він візьме форму вигину Gauss (так званої "точка"). Чим більше людей є, тим більш точний і симетричний графік буде. Це просто!
Багатозастосування чисел, що складаються з одиниць самостійно Багатомовно однакова кількість одиниць і в результаті ми отримуємо набір чисел, які слід виглядати більш уважно. Наприклад, 1111 х 1111 = 1234. У321 р.

Як бачите, результат складається з двох дзеркальних половинок, а точка симетрії в ній відповідає кількості одиниць. Знаючи це, 111111111 від 111111111 можна легко розмножувати без калькулятора і підрахувати в стовпчик. Просто напишіть цифри від 1 до 9, а потім однакову послідовність у зворотному порядку. Математика цікава і красива!
Кількість переглядів: 123456789 Якщо вам помножити кількість дев'яти послідовних цифр, то ще один цифр від 1 до 9, ви отримаєте чудовий результат.

У кожному випадку буде набір дев'яти цифр, що відповідають останню множиці і нулю в ручному місці.
Багаторазове число на 8 або 9 і додати ще одну цифру Як видно на першому фото, помножуючи числа 1, 12, 123, 1234 і так далі від 8 можна досягти дуже чудових результатів. Можливо, тому що 8 є ознакою нескінченності. Але дев'ять не блискуча гомілка. І вона має кілька сюрпризів в магазині.

На відміну від тих же чисел до 9 і додайте 1 до 9. Результатом є комплект одиниць і нуль. У той же час кількість одиниць завжди відповідатиме номеру з + знаком. Наприклад, 12345 х 9 + 5 = 111110 (+5 і п'ять нульових юнітів у відповідь).
Це лише кілька прикладів краси і симетрії математики. Немає нічого надприродного в них - звичайні математичні дії, за допомогою яких можна отримати не менше красивих номерів з красивих наборів чисел.
 р.
р.Сума чисел від 1 до 100 німецького математика, фізика та астронома Карла Гауса з дитинства мала надзвичайні здібності. Під час своєї школи він здивував своїх вчителів.

Так, один день, вчитель Карла вирішив довго тримати дітей. Він просить їх знайти суму всіх природних чисел від 1 до 100. Щоб здивувати вчителя, гаус справляється з завданням дуже швидко, знайдіть гарний візерунок, який ще використовується нами в усному обліковому записі.
1 + 2 + 3 + 4 + 5 + 6 + + 48 + 49 + 50 + 51 + 53 + 96 + 96 + 97 + 98 + 99 + 100
Дивись уважно і намагайтеся вгадати, що може бачити молодий геній. Хлопці згрупували цифри наступним чином.
1 + 100) + (2 + 99) + (3 + 98) + (4 + 97) + + (48 + 53) + (49 + 52) + (50 + 51)
50 кс 101 = 5050
В кінці він отримав 50 пар чисел, сума кожного з яких легко побачити - 101. Так сума натуральних чисел від 1 до 100 5050. Простий і елегантний рішення!

Після того, як він розвив криву, яка чітко показує розподіл ймовірностей. Це безпосередньо пов’язано не тільки з академічною наукою, але й нашим повсякденним життям. Поставимо 40 людей у своєму класі. Якщо ви зробите графік, де на осі x буде рости в сантиметрах, а на вісь буде кількість студентів з певною висотою, то він візьме форму вигину Gauss (так званої "точка"). Чим більше людей є, тим більш точний і симетричний графік буде. Це просто!
Багатозастосування чисел, що складаються з одиниць самостійно Багатомовно однакова кількість одиниць і в результаті ми отримуємо набір чисел, які слід виглядати більш уважно. Наприклад, 1111 х 1111 = 1234. У321 р.

Як бачите, результат складається з двох дзеркальних половинок, а точка симетрії в ній відповідає кількості одиниць. Знаючи це, 111111111 від 111111111 можна легко розмножувати без калькулятора і підрахувати в стовпчик. Просто напишіть цифри від 1 до 9, а потім однакову послідовність у зворотному порядку. Математика цікава і красива!
Кількість переглядів: 123456789 Якщо вам помножити кількість дев'яти послідовних цифр, то ще один цифр від 1 до 9, ви отримаєте чудовий результат.

У кожному випадку буде набір дев'яти цифр, що відповідають останню множиці і нулю в ручному місці.
Багаторазове число на 8 або 9 і додати ще одну цифру Як видно на першому фото, помножуючи числа 1, 12, 123, 1234 і так далі від 8 можна досягти дуже чудових результатів. Можливо, тому що 8 є ознакою нескінченності. Але дев'ять не блискуча гомілка. І вона має кілька сюрпризів в магазині.

На відміну від тих же чисел до 9 і додайте 1 до 9. Результатом є комплект одиниць і нуль. У той же час кількість одиниць завжди відповідатиме номеру з + знаком. Наприклад, 12345 х 9 + 5 = 111110 (+5 і п'ять нульових юнітів у відповідь).
Це лише кілька прикладів краси і симетрії математики. Немає нічого надприродного в них - звичайні математичні дії, за допомогою яких можна отримати не менше красивих номерів з красивих наборів чисел.
Чи потрібно розбити шафку на кухні, щоб отримати ручний китайський фарфоровий набір?
Фінансовий календар на грудень: купити подарунки для всіх, і без грошей