187
2021-12-01
У дочери хромает математика, нашел пример, чтобы открыть ей красоту предмета
«Правильный взгляд на математику открывает не только истину, но и безупречную красоту», — писал британский философ Бертран Рассел. А недавно стало известно, что красота математики — не просто фигура речи, а научный факт. Чтобы доказать это, ученые из Эдинбургского университета оценили мозговую активность у математиков, просматривающих изящные математические формулы. Оказалось, мозг воспринимает их точно так же, как прекрасные картины, музыку или стихи.


Так, однажды учитель Карла решил занять чем-то детей на продолжительное время. Он попросил их найти сумму всех натуральных чисел от 1 до 100. К удивлению педагога, Гаусс справился с задачей очень быстро, обнаружив красивую закономерность, которая и по сей день используется нами в устном счете.
1 + 2 + 3 + 4 + 5 + 6 + … + 48 + 49 + 50 + 51 + 52 + 53 + … + 95 + 96 + 97 + 98 + 99 + 100
Посмотри внимательно и попробуй догадаться, что же смог разглядеть юный гений? Мальчик сгруппировал числа следующим образом.
(1 + 100) + (2 + 99) + (3 + 98) + (4 + 97) + … + (48 +53) + (49 + 52) + (50 + 51)
50 х 101 = 5050
В итоге он получил 50 пар чисел, сумма каждой их которых — в чём легко убедиться — равна 101. А значит сумма натуральных чисел от 1 до 100 равна 5050. Простое и изящное решение!
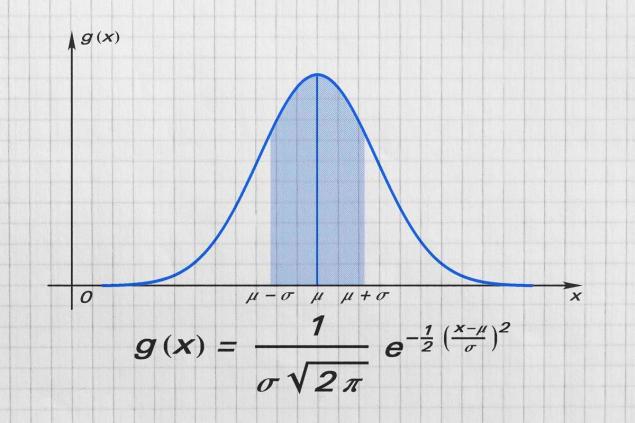
Позднее Гаусс разработал названную его именем кривую, которая наглядно отображает распределение вероятностей. Она имеет прямое отношение не только к академической науке, но и к нашей обыденной жизни. Допустим в твоем классе 40 человек. Если составить график, где по оси х будет рост в сантиметрах, а по оси у — количество учеников с тем или иным ростом, то он примет вид кривой Гаусса (так называемый «колокол»). При этом чем больше людей, тем более точным и симметричным будет получившийся график. Всё просто!

Как видно, результат состоит из двух зеркальных половинок, а точка симметрии в нём соответствует количеству единичек. Зная это, 111111111 на 111111111 можно легко перемножить без калькулятора и подсчетов в столбик. Просто пишем цифры от 1 до 9, а затем ту же последовательность в обратном порядке. Математика — это интересно и очень красиво!

В каждом случае это будет набор из девяти цифр, соответствующих последнему множителю, и нуля на предпоследнем месте.

Попробуй умножить те же числа на 9 и добавить к ним от 1 до 9. В результате получится набор из единиц и ноль. При этом количество единиц всегда будет соответствовать числу со знаком «+». Например, 12345 х 9 + 5 = 111110 ( +5 и пять единиц с нулем в ответе).
Это только несколько примеров, показывающих красоту и симметрию математики. Ничего сверхъестественного в них нет — обычные математические действия, с помощью которых из красивых наборов цифр можно получить не менее красивые числа.

Красота математики
Сумма чисел от 1 до 100
Немецкий математик, физик и астроном Карл Гаусс с детства обладал незаурядными способностями. Во время учебы в школе он не раз удивлял своих учителей.
Так, однажды учитель Карла решил занять чем-то детей на продолжительное время. Он попросил их найти сумму всех натуральных чисел от 1 до 100. К удивлению педагога, Гаусс справился с задачей очень быстро, обнаружив красивую закономерность, которая и по сей день используется нами в устном счете.
1 + 2 + 3 + 4 + 5 + 6 + … + 48 + 49 + 50 + 51 + 52 + 53 + … + 95 + 96 + 97 + 98 + 99 + 100
Посмотри внимательно и попробуй догадаться, что же смог разглядеть юный гений? Мальчик сгруппировал числа следующим образом.
(1 + 100) + (2 + 99) + (3 + 98) + (4 + 97) + … + (48 +53) + (49 + 52) + (50 + 51)
50 х 101 = 5050
В итоге он получил 50 пар чисел, сумма каждой их которых — в чём легко убедиться — равна 101. А значит сумма натуральных чисел от 1 до 100 равна 5050. Простое и изящное решение!

Позднее Гаусс разработал названную его именем кривую, которая наглядно отображает распределение вероятностей. Она имеет прямое отношение не только к академической науке, но и к нашей обыденной жизни. Допустим в твоем классе 40 человек. Если составить график, где по оси х будет рост в сантиметрах, а по оси у — количество учеников с тем или иным ростом, то он примет вид кривой Гаусса (так называемый «колокол»). При этом чем больше людей, тем более точным и симметричным будет получившийся график. Всё просто!
Умножение чисел, состоящих из единиц, на самих себя
Перемножаем одинаковое количество единичек и в результате получаем набор цифр, к которому стоит присмотреться внимательнее. К примеру, 1111 х 1111 = 1234321
Как видно, результат состоит из двух зеркальных половинок, а точка симметрии в нём соответствует количеству единичек. Зная это, 111111111 на 111111111 можно легко перемножить без калькулятора и подсчетов в столбик. Просто пишем цифры от 1 до 9, а затем ту же последовательность в обратном порядке. Математика — это интересно и очень красиво!
Умножаем число 123456789 на 9 и еще одну цифру
Если умножить число из девяти последовательных цифр на 9, а потом еще на одну цифру от 1 до 9, то получится удивительный результат.
В каждом случае это будет набор из девяти цифр, соответствующих последнему множителю, и нуля на предпоследнем месте.
Умножаем числа на 8 или 9 и добавляем еще одну цифру
Как видно на первом фото, умножением чисел 1, 12, 123, 1234 и так далее на 8 можно добиться весьма примечательных результатов. Возможно, потому, что «8» — знак бесконечности. Но и девятка не лыком шита. И у нее в запасе есть парочка сюрпризов.
Попробуй умножить те же числа на 9 и добавить к ним от 1 до 9. В результате получится набор из единиц и ноль. При этом количество единиц всегда будет соответствовать числу со знаком «+». Например, 12345 х 9 + 5 = 111110 ( +5 и пять единиц с нулем в ответе).
Это только несколько примеров, показывающих красоту и симметрию математики. Ничего сверхъестественного в них нет — обычные математические действия, с помощью которых из красивых наборов цифр можно получить не менее красивые числа.
Портал БАШНЯ. Копирование, Перепечатка возможна при указании активной ссылки на данную страницу.
Нужно ли ломать шкафчик на кухне, чтобы достать китайский фарфоровый сервиз, расписанный вручную
Финансовый календарь на декабрь: чтобы и подарки всем купить, и без денег не остаться