El hijo trajo de la escuela un problema interesante, tuvo que recordar todos los conocimientos escolares de la geometría

Esta es una de las tareas favoritas de los profesores de la Universidad de Cambridge. La mitad de los estudiantes no pueden resolverlo. Veamos si la educación es diferente en diferentes países. Y serás capaz de resolver este problema, porque matemáticas es la ciencia exacta Y las reglas son las mismas en todas partes.



La cuestión de la educación es aguda en todos los países desarrollados y sólo en los países en desarrollo del mundo. Cada año el número de gadgets y el desarrollo de la inteligencia artificial cada vez más desalienta el deseo de los niños de aprender. Dejan de pensar lógicamente, leyendo libros y desarrollando imaginación. Se hace difícil para los niños escribir, y la escritura caligráfica se ha olvidado durante mucho tiempo. Los propios niños todavía no pueden apreciar la amplitud del horror de tal pasatiempo. La tarea de los adultos es enseñar a los niños a hacer sin un teléfono en el cálculo de tareas sencillas, como esta.



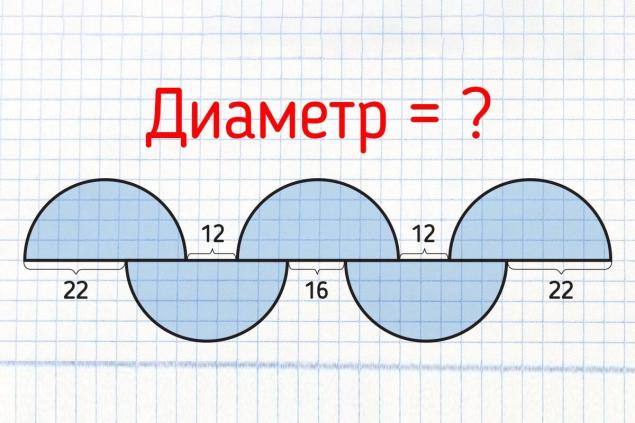
La matemática es la ciencia exacta de la perfección A primera vista parece que la tarea es muy difícil. Pero esto es sólo a primera vista. Todo lo que tienes que hacer es encontrar el diámetro del semicírculo. Los cinco semicírculos son los mismos. Y sólo conocemos algunos segmentos del diámetro del círculo. Esta tarea es manejada fácilmente por un estudiante de secundaria. ¿Pero sus padres, que se han graduado desde hace mucho tiempo de la escuela, podrán resolver este problema? Veamos lo bien que recuerdas la geometría. Si ya sabes la respuesta correcta, escríbela en los comentarios. Bueno, si el problema te causó algunas dificultades, entonces tratemos con su solución juntos.



Para empezar, sugerimos recordar desde el curso escolar de la geometría lo que son un círculo y su diámetro. Un círculo es una curva cerrada en un plano, y todos sus puntos son equidistas desde un punto dado en el centro. El punto en el centro se llama el centro del círculo. La distancia del centro al borde del círculo se llama el radio. Y el diámetro es el segmento entre los dos puntos del borde de un círculo que pasa por el centro del círculo.



Ahora regresemos a nuestro problema y hagamos una ecuación con lo desconocido. Observe que nuestros semicírculos están en ambos lados de la línea. Así que haremos la ecuación con la parte inferior y con la parte superior del eje. Denotamos cada segmento de la línea desconocida para nosotros con la letra x. Y al final, deberíamos tener esta ecuación:

22 + x + 16 + x + 22 = x + 12 + x + 12 + x

Ahora vamos a agrupar por separado cantidades conocidas y x. Y tenemos el siguiente tipo de ecuación:

(22 + 16 + 22) + (x + x) = (x + x + x) + (12 + 12)



Queda sólo para añadir cada soporte por separado y escribir una forma simplificada de la ecuación: 60 + 2x = 3x + 24

Ahora vamos a transferir los xes a un lado de la ecuación y las constantes conocidas al otro y obtener: 60 – 24 = 3 x – 2 x. Luego resta cada lado de la ecuación y consigue: 36 = x. Así, aprendimos que el diámetro de nuestro semicírculo es 36. Ahora puedes probar esta declaración sustituyendo la diferencia entre 36 y el diámetro conocido. Tienes que conseguir el mismo número de 36 en todas partes.



Si te gusta resolver problemas y ejemplos matemáticos, encontrarás muchos de ellos. La geometría y el álgebra no están sólo en la escuela. Una tarea similar puede ocurrir en la vida real. Y es bueno si lo haces bien.