The son brought from school an interesting problem, had to recall all school knowledge of geometry

This is one of the favorite tasks of Cambridge University professors. Half the students can't solve it. Let’s see if education is different in different countries. And will you be able to solve this problem, because mathematics is the exact science And the rules are the same everywhere.



The issue of education is acute in all developed and only developing countries of the world. Every year the number of gadgets and the development of artificial intelligence more and more discourages the desire of children to learn. They stop thinking logically, reading books, and developing imagination. It becomes difficult for children to write, and calligraphic handwriting has long been forgotten. Children themselves are not yet able to appreciate the full extent of the horror of such a pastime. The task of adults is to teach children to do without a phone in the calculation of simple tasks, such as this.



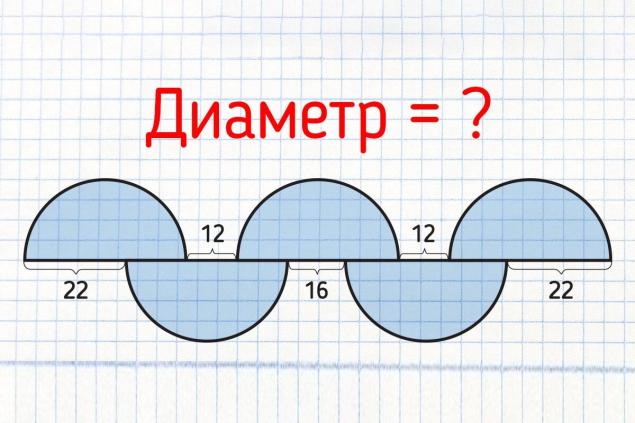
Mathematics is the exact science of perfection At first glance it seems that the task is very difficult. But this is only at first glance. All you have to do is find the diameter of the semicircle. All five semicircles are the same. And we know only some segments of the diameter of the circle. This task is easily handled by a high school student. But will his parents, who have long since graduated from school, be able to solve this problem? Let's see how well you remember geometry. If you already know the correct answer, write it to us in the comments. Well, if the problem caused you some difficulties, then let's deal with its solution together.

198917

To begin with, we suggest remembering from the school course of geometry what a circle and its diameter are. A circle is a closed curve on a plane, and all its points are equidistant from a given point in the center. The point in the center is called the center of the circle. The distance from the center to the edge of the circle is called the radius. And the diameter is the segment between the two points of the edge of a circle that passes through the center of the circle.



Now let us return to our problem and make an equation with the unknown. Notice our semicircles are on both sides of the line. So we will make the equation with the lower part and with the upper part of the axis. Let’s denote each segment of the line unknown to us with the letter x. And in the end, we should have this equation:

22 + x + 16 + x + 22 = x + 12 + x + 12 + x

Now let us group separately known quantities and x. And we get the following kind of equation:

(22 + 16 + 22) + (x + x) = (x + x + x) + (12 + 12)



It remains only to add each bracket separately and write down a simplified form of the equation: 60 + 2x = 3x + 24

Now let’s transfer the xes to one side of the equation and the known constants to the other and get: 60 – 24 = 3 x – 2 x. Then subtract each side of the equation and get: 36 = x. Thus, we learned that the diameter of our semicircle is 36. Now you can test this statement by substituting the difference between 36 and the known diameter. You have to get the same number of 36 everywhere.



If you like to solve problems and mathematical examples, you will find a lot of them. Geometry and algebra are not just in school. A similar task can occur in real life. And it's good if you get it right.