165
年轻的波森通过游戏解决了输血问题, 成人科学医生不能
法国数学家西梅翁·德尼·普瓦松(英语:Simeon Denis Poisson)在选择人生道路方面犹豫了很长时间. 直到一个朋友向他展示了在船只之间转换出水分的巧妙任务,他无法自行解决. 年轻的普瓦松在不到一个小时的时间里找到了一个解决方案. 因此他决定成为数学家. 界定他生活的任务被称为"普瓦生问题".
 (英语).
(英语).
今天,这种任务最为广泛。 可以在Google和微软的访谈中找到. 威利斯的英雄甚至与其中一人相遇, 你能像普森和约翰·麦克兰那样轻松地处理输血任务吗? 一个小的破坏者:我们将展示如何用编程和台球原理来玩弄解决普瓦生问题.
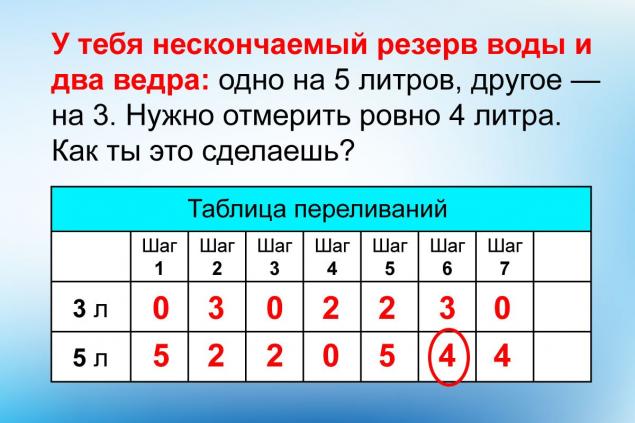
Poisson 任务是微软的测试任务 “你们有无尽的储备水和两桶:一桶为五升,一桶为三升。” 我们需要精确地测量出4升. 或快 让我们开始思考 像威利斯的优秀电影英雄。
 (英语).
(英语).
显然,4升不会装入更小的桶中。 因此,我们最初填充了五升水. 然后把一个更小的桶装进去是合乎逻辑的。 现在小桶已满了,而大桶有2升. 还有... 暂停 牢记所有可能的选择都变得困难。 因此,只有少数人能够通过试验和错误解决问题. 但是在灵感失败的地方,算法有帮助. 如足球运动员所言,秩序胜于阶级.
我们给微软的求职者带来了好消息。 现在,为了解决输血问题,它足以记住一系列简单的行动。 在宣布之前, 让我们看看用两桶可以做什么。 让我们叫他们命令,并分配每个缩略名.
NB - 装入大容器中的水
NM - 填补较小的容量
NB - 空出一个更大的容器
NM - 空出较小的容器
PBM - 从大型容器倒入小型容器
PMB - 将水从更小的容器转移到更大的容器
血压? 检查一个更大的容器是否满了
检查较小的容器是否为空 。
为了方便,我们将实行另一种削减。 我们同意将水桶中的水量记录为:y,在更小的桶中放入一升水,而y在更大的桶中放入一升水。 例如:2:5的记录将意味着更小的桶为2升,而更大的桶被完全填充.
 (英语).
(英语).
现在用图上的流程图 起初,两桶都是空的,所以我们会写出0-0. 装上小桶,我们得到3-0。 我们从少到多,结果结果是:0:3. 然后我们冷静地遵循这个计划,而不用担心任何事情。 它和瑞士刀一样简单可靠. 所有行动的记录如下:
0:0 - 3:0 - 0:3 - 3:3 - 1:5 - 1:0 - 0:1 - 3:1 - 0:4(!)
唯一的缺点是,根据这个方案找到的解决办法并不总是最合理的。 例如,“坚果”需要减少两个步骤。 他从一个更大的桶起步,成功融入了6个输液.
0:0 - 0:5 - 3:2 - 0:2 - 2:0 - 2:5 - 3:4(!)
台球是否是智力游戏的问题仍未解决. 但事实上,在游戏的原则上,解决普瓦生问题的方法被构建起来,这说明很多事情. 幸运的是,我们不需要一个提示。 我们将用一张平面图形式的平面桌子来滚动球。
第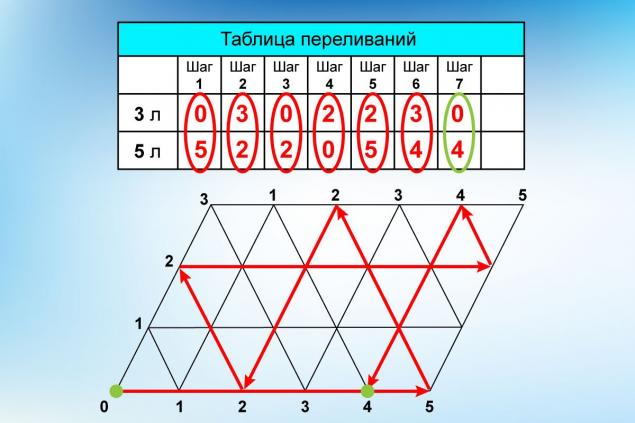 号
号
可以看到,应用到它的行会形成一个相同的三角形的网格. 瞷秨_钡 三角形的顶点与我们的“表”相接的地方以数字表示。 同时,横向显示五升船体的水量,并垂直显示- 三升船体.
 (英语).
(英语).
皮尔 所以,让我们开始球! 最初它位于左下角并被撞击后沿平行图下侧移动到"5"点. 这意味着我们完全装满了更大的水桶 然后球弹到一个点 坐标是水平2,垂直3。 这意味着更小的桶被完全填满,而更大的桶还剩下2升.
在追踪了球的更远的路径并记录了球的所有运动阶段之后,我们得到了同样的解决方案,这是麦凯恩提出的. 如果从0点开始 球在短边滚? 你自己试试确定你的决定 只需要再走两步 就像我们第一次尝试流程图一样
该是应对挑战的时候了,挑战永远地改变了德尼·普森的生活. 谁知道,也许如果你解决了它, 你也会发现数学的美丽?
 (英语).
(英语).
“一人一桶有12品脱的蜂蜜,想将蜂蜜分出一半,但他没有6品脱的容器,但有两个由8品脱和5品脱组成的空容器。 如何用来倒满6品脱的蜂蜜?
普瓦生是如何解决这个问题的还不知道。 但读了我们的文章后 你用我所希望的 更容易获得的知识武装自己 你可以选择两种方法之一 开始工作!
不要忘记,我们现在拥有的体积较小的容器有5升,体积更大 -- -- 8升。 我决定使用流程图,并在18个动作后做出决定.
0:0 - 5:0 - 0:5 - 5:5 - 2:8 - 2:0 - 0:2 - 5:2 - 5:7 - 4:8 - 4:0 - 0:4 - 5:4 - 1:8 - 1:0 - 1 - 0:6 (!)
然而,这一行动方针可能并非最理想。 所以,你有机会仔细思考 找出最好的方案。 毕竟,输血任务有助于我们发展逻辑思维、想象力和毅力。 想象一下自己在普瓦森的位置 并在评论中分享你的发现
 (英语).
(英语).今天,这种任务最为广泛。 可以在Google和微软的访谈中找到. 威利斯的英雄甚至与其中一人相遇, 你能像普森和约翰·麦克兰那样轻松地处理输血任务吗? 一个小的破坏者:我们将展示如何用编程和台球原理来玩弄解决普瓦生问题.
Poisson 任务是微软的测试任务 “你们有无尽的储备水和两桶:一桶为五升,一桶为三升。” 我们需要精确地测量出4升. 或快 让我们开始思考 像威利斯的优秀电影英雄。
 (英语).
(英语).显然,4升不会装入更小的桶中。 因此,我们最初填充了五升水. 然后把一个更小的桶装进去是合乎逻辑的。 现在小桶已满了,而大桶有2升. 还有... 暂停 牢记所有可能的选择都变得困难。 因此,只有少数人能够通过试验和错误解决问题. 但是在灵感失败的地方,算法有帮助. 如足球运动员所言,秩序胜于阶级.
我们给微软的求职者带来了好消息。 现在,为了解决输血问题,它足以记住一系列简单的行动。 在宣布之前, 让我们看看用两桶可以做什么。 让我们叫他们命令,并分配每个缩略名.
NB - 装入大容器中的水
NM - 填补较小的容量
NB - 空出一个更大的容器
NM - 空出较小的容器
PBM - 从大型容器倒入小型容器
PMB - 将水从更小的容器转移到更大的容器
血压? 检查一个更大的容器是否满了
检查较小的容器是否为空 。
为了方便,我们将实行另一种削减。 我们同意将水桶中的水量记录为:y,在更小的桶中放入一升水,而y在更大的桶中放入一升水。 例如:2:5的记录将意味着更小的桶为2升,而更大的桶被完全填充.
 (英语).
(英语).现在用图上的流程图 起初,两桶都是空的,所以我们会写出0-0. 装上小桶,我们得到3-0。 我们从少到多,结果结果是:0:3. 然后我们冷静地遵循这个计划,而不用担心任何事情。 它和瑞士刀一样简单可靠. 所有行动的记录如下:
0:0 - 3:0 - 0:3 - 3:3 - 1:5 - 1:0 - 0:1 - 3:1 - 0:4(!)
唯一的缺点是,根据这个方案找到的解决办法并不总是最合理的。 例如,“坚果”需要减少两个步骤。 他从一个更大的桶起步,成功融入了6个输液.
0:0 - 0:5 - 3:2 - 0:2 - 2:0 - 2:5 - 3:4(!)
台球是否是智力游戏的问题仍未解决. 但事实上,在游戏的原则上,解决普瓦生问题的方法被构建起来,这说明很多事情. 幸运的是,我们不需要一个提示。 我们将用一张平面图形式的平面桌子来滚动球。
第
 号
号可以看到,应用到它的行会形成一个相同的三角形的网格. 瞷秨_钡 三角形的顶点与我们的“表”相接的地方以数字表示。 同时,横向显示五升船体的水量,并垂直显示- 三升船体.
 (英语).
(英语).皮尔 所以,让我们开始球! 最初它位于左下角并被撞击后沿平行图下侧移动到"5"点. 这意味着我们完全装满了更大的水桶 然后球弹到一个点 坐标是水平2,垂直3。 这意味着更小的桶被完全填满,而更大的桶还剩下2升.
在追踪了球的更远的路径并记录了球的所有运动阶段之后,我们得到了同样的解决方案,这是麦凯恩提出的. 如果从0点开始 球在短边滚? 你自己试试确定你的决定 只需要再走两步 就像我们第一次尝试流程图一样
该是应对挑战的时候了,挑战永远地改变了德尼·普森的生活. 谁知道,也许如果你解决了它, 你也会发现数学的美丽?
 (英语).
(英语).“一人一桶有12品脱的蜂蜜,想将蜂蜜分出一半,但他没有6品脱的容器,但有两个由8品脱和5品脱组成的空容器。 如何用来倒满6品脱的蜂蜜?
普瓦生是如何解决这个问题的还不知道。 但读了我们的文章后 你用我所希望的 更容易获得的知识武装自己 你可以选择两种方法之一 开始工作!
不要忘记,我们现在拥有的体积较小的容器有5升,体积更大 -- -- 8升。 我决定使用流程图,并在18个动作后做出决定.
0:0 - 5:0 - 0:5 - 5:5 - 2:8 - 2:0 - 0:2 - 5:2 - 5:7 - 4:8 - 4:0 - 0:4 - 5:4 - 1:8 - 1:0 - 1 - 0:6 (!)
然而,这一行动方针可能并非最理想。 所以,你有机会仔细思考 找出最好的方案。 毕竟,输血任务有助于我们发展逻辑思维、想象力和毅力。 想象一下自己在普瓦森的位置 并在评论中分享你的发现























