Young Poisson solucionó el problema con la transfusión juguetona, y los médicos adultos de la ciencia no pueden

El matemático francés Simeon Denis Poisson dudó mucho tiempo en su elección del camino de la vida. Hasta que un amigo le mostró la ingeniosa tarea de transfundir agua entre los vasos, que no podía resolverse. Young Poisson encontró una solución en menos de una hora. Como resultado, decidió convertirse en matemático. La tarea que definía su vida se llamaba el Problema de Poisson.



Hoy en día, tales tareas son más generalizadas. Se pueden encontrar en entrevistas en Google y Microsoft. Y con uno de ellos, el héroe de Willis incluso se encuentra en la pantalla del blockbuster Hollywood “Die Hard 3”. ¿Puedes manejar la tarea de transfusión tan fácilmente como Poisson y John McClain? Un pequeño spoiler: vamos a mostrar cómo resolver el problema de Poisson con los principios de programación y billar.

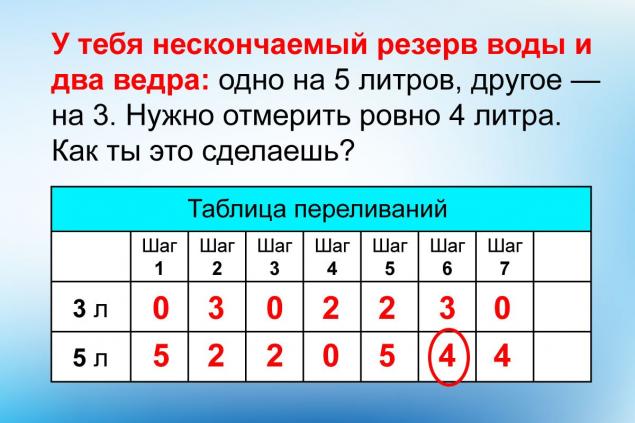
La tarea Poisson es una tarea de prueba de Microsoft “Tienes una reserva sin fin de agua y dos cubos: uno para 5 litros, el otro para 3.” Necesitamos medir exactamente 4 litros. ¿Cómo lo harás? Empecemos a pensar como el héroe de la película de Willis.



Obviamente, 4 litros no encajarán en un cubo más pequeño. Así que inicialmente llenamos el agua de cinco litros. Entonces sería lógico llenar un cubo más pequeño de él. Ahora el cubo pequeño está lleno, y el grande tiene 2 litros. Y... pausa. Mantener todas las opciones posibles en mente se hace difícil. Por lo tanto, sólo unas pocas personas pueden resolver el problema por juicio y error. Pero donde falla la inspiración, el algoritmo ayuda. Como dicen los futbolistas, el orden gana clase.

Tenemos buenas noticias para los buscadores de empleo en Microsoft. Ahora, para resolver el problema de la transfusión, es suficiente recordar una simple serie de acciones. Pero antes de anunciarlo, veamos qué puedes hacer con dos cubos. Vamos a llamarlos comandos y asignar cada designación abreviada.

NB - llenar un gran contenedor con agua
NM - llenar una capacidad más pequeña
NB - vaciar un vaso más grande
NM - vaciar el vaso más pequeño
PBM - verter agua de un vaso grande en uno más pequeño
PMB – transferir agua de un vaso más pequeño a uno más grande
¿BP? – Compruebe si un vaso más grande está lleno
Revise si el vaso más pequeño está vacío.

Para mayor comodidad, introduciremos otra reducción. Estamos de acuerdo en registrar la cantidad de agua en cubos como :y, donde los litros de agua en un cubo más pequeño, y y en uno más grande. Por ejemplo, un registro de 2:5 significará que el cubo más pequeño es de 2 litros, y el mayor está completamente lleno.



Ahora usemos el diagrama de flujo del dibujo. Inicialmente, ambos cubos están vacíos, así que escribiremos 0-0. Llena el cubo más pequeño, tenemos 3-0. Pasamos de menos a más, resulta 0: 3. Luego seguimos tranquilamente el esquema sin preocuparse por nada. Es tan simple y confiable como un cuchillo suizo. A continuación figura un registro de todas las acciones.

0:0 - 3:0 - 0:3 - 3:3 - 1:5 - 1:0 - 0:1 - 3:1 - 0:4(!)

El único inconveniente es que la solución encontrada según este esquema no siempre será la más racional. Por ejemplo, la “nuez dura” necesitaba dos movimientos menos. Comenzó con un cubo más grande y logró encajar en seis transfusiones.

0:0 - 0:5 - 3:2 - 0:2 - 2:0 - 2:5 - 3:4(!)

La cuestión de si billar es un juego intelectual sigue abierta. Pero el hecho de que en los principios del juego, se construye el método de resolver el problema Poisson dice mucho. Afortunadamente, no necesitaremos una señal. Rodearemos las bolas virtualmente usando una tabla dibujada en forma de un paralelograma.



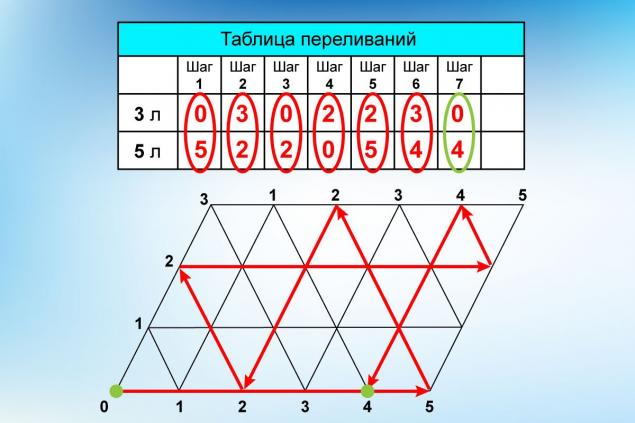
Como puede ver, las líneas aplicadas a ella forman una cuadrícula de triángulos idénticos. Ahora para las designaciones. Los lugares donde los vértices de los triángulos entran en contacto con los lados de nuestra “tabla” se indican por números. Al mismo tiempo, se muestra horizontalmente la cantidad de agua en un recipiente de cinco litros y verticalmente en un recipiente de tres litros.



Peels ¡Empecemos la pelota! Inicialmente, estaba en la esquina inferior izquierda y después del impacto se movía a lo largo del lado inferior del paralelograma al punto "5". Eso significa que hemos llenado un cubo más grande con agua. Luego la bola rebota a un punto con coordenadas 2 horizontalmente y 3 verticalmente. Esto significa que el cubo más pequeño está completamente lleno, y el mayor tiene 2 litros dejados.

Después de haber rastreado el camino más profundo de la bola y grabado todas las etapas de su movimiento, obtenemos la misma solución, con la que McCain surgió. ¿Y si desde el punto 0 la bola rodó en el lado corto? Pruébalo tú mismo para asegurarte de tomar una decisión. Va a tomar dos movimientos más, como en nuestro primer intento con el diagrama de flujo.

Es hora de enfrentar el desafío que cambió la vida de Denis Poisson para siempre. ¿Quién sabe, tal vez si lo resuelves, también descubrirás la belleza de las matemáticas?

688050

“Una persona tiene 12 pintas de miel en un barril y quiere dar la mitad de la miel, pero no tiene un vaso de 6 pintas, pero hay dos vasos vacíos de 8 pintas y 5 pintas. ¿Cómo utilizarlos para verter exactamente 6 pintas de miel?

No se sabe cómo Poisson solucionó este problema. Pero después de leer nuestro artículo, te has armado con el conocimiento de que espero que sea más fácil. ¡Puedes elegir uno de dos métodos y trabajar!

No olvide que el vaso más pequeño ahora tenemos un volumen de 5 litros, y el mayor - 8 litros. Decidí usar el diagrama de flujo y llegué a una decisión después de 18 movimientos.

0:0 - 5:0 - 0:5 - 5:5 - 2:8 - 2:0 - 0:2 - 5:2 - 0:7 - 5:7 - 4:8 - 4:0 - 0:4 - 5:4 - 1:8 - 1:0 - 0:1 - 5:1 - 0:6 (!)

Sin embargo, este curso de acción probablemente no es el más óptimo. Así que tienes la oportunidad de pensar duro para descubrir el mejor esquema. Después de todo, las tareas de transfusión nos ayudan a desarrollar el pensamiento lógico, la imaginación y la perseverancia. Imagínate en el lugar de Poisson y comparte tu descubrimiento en los comentarios.