Юный Пуассон решил задачу с переливанием играючи, а взрослые доктора наук не могут

Французский математик Симеон Дени Пуассон долго колебался в выборе жизненного пути. Пока друг не показал ему хитроумную задачу на переливание воды между сосудами, которую никак не мог решить сам. Юный Пуассон нашел решение меньше чем за час. И в результате твердо решил стать математиком. А задача, которая определила его жизнь, получила название «Задача Пуассона».



Сегодня подобные задачи получили самое широкое распространение. Их можно встретить на собеседованиях в Google и Microsoft. А с одной из них герой Уиллиса даже сталкивается на экране голливудского блокбастера «Крепкий орешек 3». Сможешь ли ты справиться с задачей на переливание так же легко, как это сделали Пуассон и Джон Макклейн? Небольшой спойлер: мы покажем, как играючи решить задачу Пуассона, используя принципы программирования и… бильярда.

Задача Пуассона

Тестовое задание от Microsoft

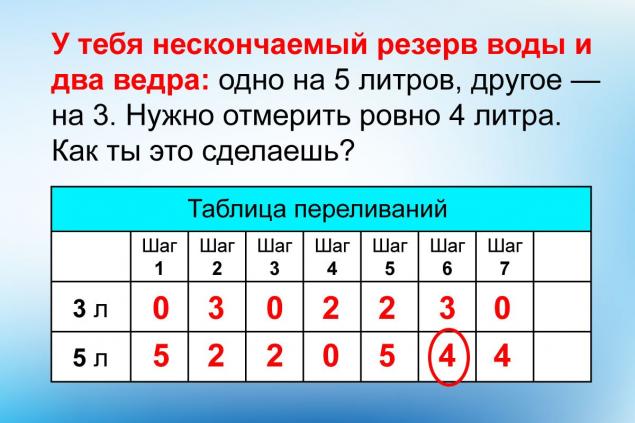
«У тебя нескончаемый резерв воды и два ведра: одно на 5 литров, другое — на 3. Нужно отмерить ровно 4 литра. Как ты это сделаешь?» Начнем рассуждать, как смекалистый киногерой Виллиса.



Очевидно, что 4 литра не влезет в меньшее ведро. Значит изначально заполняем водой пятилитровое. Дальше логичным будет наполнить из него меньшее ведро. Теперь маленькое ведро заполнено полностью, а в большом остается 2 литра. И… пауза. Удержать в уме все возможные варианты становится сложно. Поэтому решить задачу методом проб и ошибок под силу лишь немногим. Но там, где не справляется вдохновение, выручает алгоритм. Как говорят футболисты, порядок бьет класс.

Метод блок-схем

У нас хорошая новость для соискателей должности в Microsoft. Теперь для решения задачи на переливание достаточно запомнить несложный ряд действий. Но перед тем, как его огласить, посмотрим какие действия вообще можно предпринять с двумя ведрами. Назовем их командами и присвоим каждой сокращенное обозначение.

НБ — наполнить водой большую емкость
НМ — наполнить меньшую емкость
НБ — опорожнить больший сосуд
НМ — опорожнить меньший сосуд
ПБМ — перелить воду из большого сосуда в меньший
ПМБ — перелить воду из меньшего сосуда в больший
БП? — проверить заполнен ли больший сосуд
МО? — проверить опорожнен ли меньший сосуд

Для удобства введем еще одно сокращение. Условимся записывать количество воды в ведрах в виде :y, где — литров воды в меньшем ведре, а у — в большем. Так, например, запись 2:5 будет означать, что в меньшем ведре 2 литра, а большее заполнено полностью.



Теперь воспользуемся блок-схемой с рисунка. Изначально оба ведра пусты, значит запишем 0:0. Наполняем меньшее ведро, получается 3:0. Переливаем из меньшего в большее, получается 0:3. Дальше спокойно следуем схеме, ни о чём не переживая. Метод прост и надежен, как швейцарский нож. А запись всех действий приведена ниже.

0:0 — 3:0 — 0:3 — 3:3 — 1:5 — 1:0 — 0:1 — 3:1 — 0:4(!)

Единственный минус, что найденное по такой схеме решение не всегда будет самым рациональным. Например, «крепкому орешку» понадобилось на целых два хода меньше. Как мы уже писали, он начал с большего ведра и сумел уложиться в шесть переливаний.

0:0 — 0:5 — 3:2 — 0:2 — 2:0 — 2:5 — 3:4(!)

Метод математического бильярда

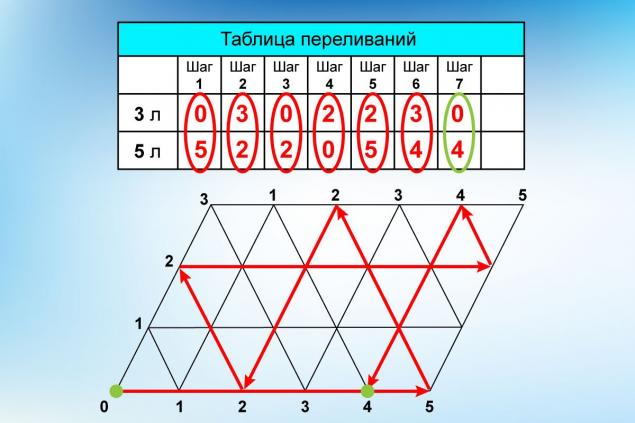
Вопрос является ли бильярд интеллектуальной игрой остается открытым. Но то, что на принципах игры, построен метод решения задачи Пуассона, говорит о многом. К счастью, нам не понадобится кий. Катать шары мы будем виртуально, используя нарисованный стол в форме параллелограмма.



Как видишь, нанесенные на него прямые образуют сетку из одинаковых треугольников. Теперь об обозначениях. Места, где вершины треугольников соприкасаются со сторонами нашего «стола» обозначены цифрами. При этом по горизонтали отображается количество воды в пятилитровом, а по вертикали — в трехлитровом сосуде.



Peels Итак, запускаем шар! Изначально он находился в левом нижнем углу и после удара переместился вдоль нижней стороны параллелограмма до точки «5». Это значит, что мы полностью наполнили водой большее ведро. Затем шар отскакивает в точку с координатами 2 по горизонтали и 3 по вертикали. Это значит, что меньшее ведро заполнено полностью, а в большем осталось 2 литра.

Проследив дальнейший путь шара и записав все этапы его движения, получаем то же решение, до которого додумался Маккейн. А если бы из точки «0» шар покатился бы по короткой стороне? Попробуй сам, чтобы убедиться, что тоже придешь к решению. Просто понадобится на два хода больше, как в нашей первой попытке с помощью блок-схемы.

Задача, которая прославила Пуассона

Пришло время заняться задачей, которая навсегда изменила жизнь Дени Пуассона. Как знать, может решив ее, ты тоже откроешь для себя красоту математики?



«Один человек имеет в бочонке 12 пинт меда и хочет подарить половину меда, но у него нет сосуда в 6 пинт, однако имеются два пустых сосуда объемом 8 пинт и 5 пинт. Как с их помощью отлить ровно 6 пинт меда?»

Доподлинно неизвестно, как эту задачу решал Пуассон. Но, прочитав нашу статью, ты вооружился знанием, которое, надеюсь, облегчит задачу. Можешь выбрать один из двух методов и за работу!

Решение задачи Пуассона

Не забывай, что меньший сосуд у нас теперь имеет объем 5 литров, а больший — 8 литров. Я решил воспользоваться блок-схемой и пришел к решению после 18 ходов.

0:0 — 5:0 — 0:5 — 5:5 — 2:8 — 2:0 — 0:2 — 5:2 — 0:7 — 5:7 — 4:8 — 4:0 — 0:4 — 5:4 — 1:8 — 1:0 — 0:1 — 5:1 — 0:6(!)

Однако этот порядок действий наверняка не самый оптимальный. Так что у тебя есть шанс хорошенько подумать, чтобы вычислить лучшую схему. Ведь задачи на переливание помогают нам развивать логическое мышление, воображение и настойчивость. Представь себя на месте Пуассона и поделись своим открытием в комментариях.