Young Poisson solved the problem with transfusion playfully, and adult doctors of science can not

The French mathematician Simeon Denis Poisson hesitated for a long time in his choice of life path. Until a friend showed him the ingenious task of transfusing water between vessels, which he could not solve himself. Young Poisson found a solution in less than an hour. As a result, he decided to become a mathematician. The task that defined his life was called the Poisson Problem.



Today, such tasks are most widespread. They can be found in interviews at Google and Microsoft. And with one of them, the hero of Willis even encounters on the screen of the Hollywood blockbuster “Die Hard 3”. Can you handle the transfusion task as easily as Poisson and John McClain did? A small spoiler: we will show how to playfully solve the Poisson problem using the principles of programming and billiards.

The Poisson task is a test task from Microsoft “You have an endless reserve of water and two buckets: one for 5 liters, the other for 3.” We need to measure exactly 4 liters. How will you do that? Let's start thinking like Willis' savvy movie hero.



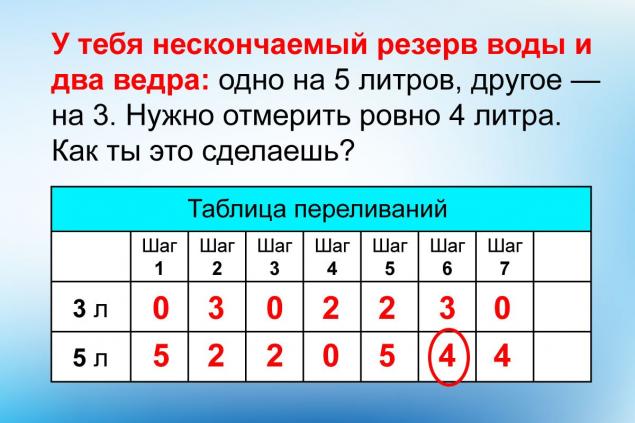
Obviously, 4 liters will not fit into a smaller bucket. So we initially fill the five-liter water. Then it would be logical to fill a smaller bucket out of it. Now the small bucket is full, and the large one has 2 liters. And -- pause. Keeping all possible options in mind becomes difficult. Therefore, only a few people can solve the problem by trial and error. But where inspiration fails, the algorithm helps. As footballers say, order beats class.

We have good news for job seekers at Microsoft. Now, to solve the transfusion problem, it is enough to remember a simple series of actions. But before we announce it, let’s see what you can do with two buckets. Let's call them commands and assign each abbreviated designation.

NB - fill a large container with water
NM - fill a smaller capacity
NB - empty a larger vessel
NM - empty the smaller vessel
PBM - pour water from a large vessel into a smaller one
PMB – transfer water from a smaller vessel to a larger one
BP? – Check if a larger vessel is full
Check if the smaller vessel is empty.

For convenience, we will introduce another reduction. We agree to record the amount of water in buckets as :y, where liters of water in a smaller bucket, and y in a larger one. For example, a record of 2:5 will mean that the smaller bucket is 2 liters, and the larger is fully filled.



Now let's use the flowchart from the drawing. Initially, both buckets are empty, so we will write 0-0. Fill the smaller bucket, we get 3-0. We turn from less to more, it turns out 0: 3. Then we calmly follow the scheme without worrying about anything. It is as simple and reliable as a Swiss knife. A record of all actions is given below.

0:0 - 3:0 - 0:3 - 3:3 - 1:5 - 1:0 - 0:1 - 3:1 - 0:4(!)

The only drawback is that the solution found according to this scheme will not always be the most rational. For example, the “hard nut” needed two fewer moves. He started with a larger bucket and managed to fit into six transfusions.

0:0 - 0:5 - 3:2 - 0:2 - 2:0 - 2:5 - 3:4(!)

The question of whether billiards is an intellectual game remains open. But the fact that on the principles of the game, the method of solving the Poisson problem is built says a lot. Fortunately, we won't need a cue. We will roll the balls virtually using a drawn table in the form of a parallelogram.



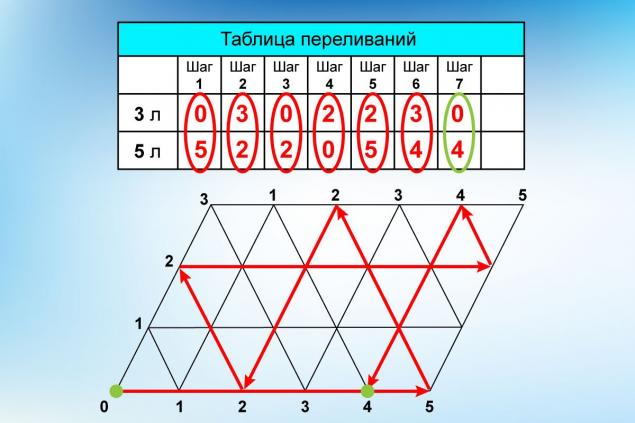
As you can see, the lines applied to it form a grid of identical triangles. Now for the designations. The places where the vertices of the triangles come into contact with the sides of our “table” are indicated by numbers. At the same time, horizontally the amount of water in a five-liter vessel is displayed, and vertically - in a three-liter vessel.

617480

Peels So let's start the ball! Initially, it was in the lower left corner and after the impact moved along the lower side of the parallelogram to the point "5". That means we've completely filled a larger bucket with water. Then the ball bounces to a point with coordinates 2 horizontally and 3 vertically. This means that the smaller bucket is fully filled, and the larger one has 2 liters left.

Having traced the further path of the ball and recorded all the stages of its movement, we get the same solution, which McCain came up with. What if from point 0 the ball rolled on the short side? Try it yourself to make sure you come to a decision. It's just going to take two more moves, like in our first attempt with the flowchart.

It's time to tackle the challenge that changed Denis Poisson's life forever. Who knows, maybe if you solve it, you will also discover the beauty of mathematics?



“One person has 12 pints of honey in a barrel and wants to give half the honey, but he does not have a 6 pint vessel, but there are two empty vessels of 8 pints and 5 pints. How to use them to pour exactly 6 pints of honey?

It is not known how Poisson solved this problem. But after reading our article, you've armed yourself with knowledge that I hope will make it easier. You can choose one of two methods and get to work!

Do not forget that the smaller vessel we now have a volume of 5 liters, and the larger - 8 liters. I decided to use the flowchart and came to a decision after 18 moves.

0:0 - 5:0 - 0:5 - 5:5 - 2:8 - 2:0 - 0:2 - 5:2 - 0:7 - 5:7 - 4:8 - 4:0 - 0:4 - 5:4 - 1:8 - 1:0 - 0:1 - 5:1 - 0:6 (!)

However, this course of action is probably not the most optimal. So you have a chance to think hard to figure out the best scheme. After all, transfusion tasks help us develop logical thinking, imagination and perseverance. Imagine yourself in Poisson's place and share your discovery in the comments.