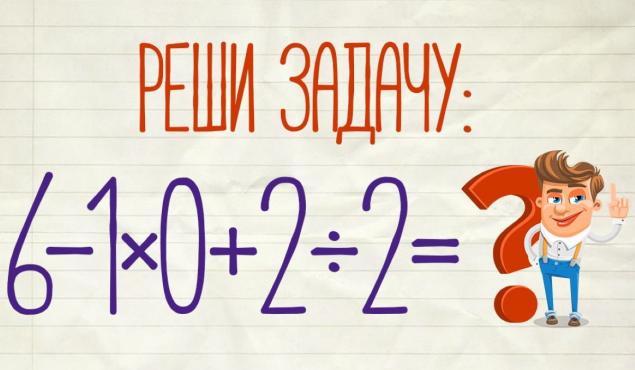Математичний приклад впливу солодкої ностальгії на шкільні уроки

Дорослим, як претендувати, вони знають все. Але якщо дитина просить допомогти з уроками, то швидше за все, отримати відмову від розумної допомоги. Звісно, ті дядьки і тітки, які добре робили в школі, напевно, вирішили все. Пазлий Але скільки? Ми пропонуємо перевірку.

Сьогодні видання. "Сайт" Ми можемо самі зателефонувати одержувачу. Хороший спосіб перевірити себе і дізнатися, чи є мозок в хорошій формі, і чи здатний вирішити проблемні проблеми.



Математичні головоломки Умови та питання

1. Це, здається, бути простий Це викликало багато обговорення в Інтернеті. Це тому, що різні читачі мають різні відповіді. Хто вважає, що правильний відповідь 5. Інші стверджують, що в кінці він повинен бути блоком. На відміну від інших наполягають, що 7 був правильний результат. Хто правильно? Або відповідь повністю відрізняється?
   
   
   
   
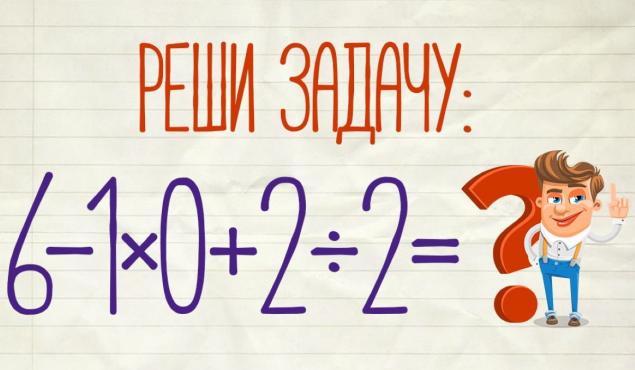
2. Якщо було можливо легко зрозуміти першу задачу, то ми пропонуємо проблему, де потрібно ввімкнути логіку і ретельно продумати. Вона сказала, що один раз, коли лицар був захоплений Султаном. Він сказав, що він випустить в'язницю і його кінь, якщо він отримав масивний рансом 30,000 золоті монети. Не було грошей, а не багатих родичів, тому він вирішив обдурити. «О могутній салатин, ви не надії. У рідній країні кожен смарт-в'язень дає можливість вільно бути. Він пропонує головоломку. Якщо він вирішить - стає безкоштовним, якщо він не вирішує - кількість рансом подвоюється, про що сказав він.
   
   Салатин коханих головоломок, тому він любив пропозицію в'язниці.
   
   «Окай, нехай це так. Ось ваша проблема. Завтра вранці ви будете давати дванадцяти однакових монет і простий масштаб без ваги. Одна монета буде підробкою. Але ніхто не знає, якщо це легше або важче інших. Ви будете мати три зважування, щоб визначити підробку. Якщо ви не можете це зробити, це погано для вас.
   
   Як знайти підроблену монету серед 12 монет в 3 ваги? Чи можливо це зробити?
   
   1900 р.
   
   
   
   

Відповіді на головоломки

1. Для вирішення цього прикладу необхідно пам'ятати шкільне правило, яке ми спочатку виконуємо багатозастосування і поділ, а тільки потім додавання і відступ. Якщо так, наш приклад займе наступну форму: 6 - 1 * 0 + 2 = 6 - 0 + 1 = 7.
   
   
2. Друга проблема буде приймати довше для вирішення. Ускладнюючи це те, що ми не знаємо за умови, що монета важче: підроблені або реальні. Невідомо, чи вдалося з'ясувати відповідь до ранку. Давайте спробуємо зробити це для нього.
   
   
   
   По-перше, розділіть монети на 3 рівні запікання 4 монети. Ми зважимо перші дві партії монет. Якщо вони рівні за вагоюТак ми щасливі, і підроблена монета в третій палі.
   
   Потім зважали будь-які дві реальні монети (у першу і другу партію) і дві монети з останньої палі, де була одна підробка. Якщо шкали знову показують рівноправність, то підроблена монета є однією з решти двох (з них ми не доторкнулися).
   
   Таким чином, в третьому крокі зважати одну з реальних монет, ми вже знаємо як з решти двох. Якщо рівноправність знову, то підроблена монета є одним, ми не доторкнулися. Якщо не існує рівності, то також знайдено підробку. У той же час ми дізнаємося, чи важка, ніж оригінальна або запальна.
   
   Якщо нерівність в другому зважуванні пара з фейкою знайдена. Пошук підробленої монети для третього зважування знову не складе труднощів.
   
   
   
   
   
   Якщо при першому зваженні Одна група була важка, тому була підроблена монета в першій вісімці. Ймовірно в цьому випадку краще буде число всіх монет: перша кришка (печей) - 1,2,3,4; другий (світло) - 5,6,7,8; третій (реальний) - 9,10,11,12.
   
   Другий крок - зважити монети 1.9,10,11 і 2.3,4,5. Якщо рівність є помилковим 6.7 або 8. У той же час після першого зважування ми вже дізналися, що друга партія легше. Так підробка легше, ніж оригінальна. Так важить 6 і 7. Скільки простіше підробки. Якщо монета дорівнює рівній, підроблена монета 8.
   
   Якщо після другого кроку ми побачили, що група 1.9,10,11 важче, ніж група 2.3,4,5, то помилкова група є або 1 (зважувачем) або 5 (світильник). Досить зважити, сказати, 1 і будь-яку реальну монету. Якщо 1 важче, це підробка. Якщо рівність, то підробка є 5.
   
   Якщо група 2,3,4,5, це означає, що монета підробки важче, і це серед 2,3,4. У цьому випадку важить, наприклад, 2 і 3. Це важко, це підробка. Якщо монета рівна, то монета під номером 4 буде помилковою.
   
   
   
   
   
   

Зроби! Останній виклик був непросто. Звісно, це буде можливо спростити його, змінивши оригінальні умови, але це буде справедливим? Я сподіваюсь, що лицар також вдалося вирішити його, бо він явно мав більш мотивацію. Або можливо, є простий спосіб, який він знайшов?