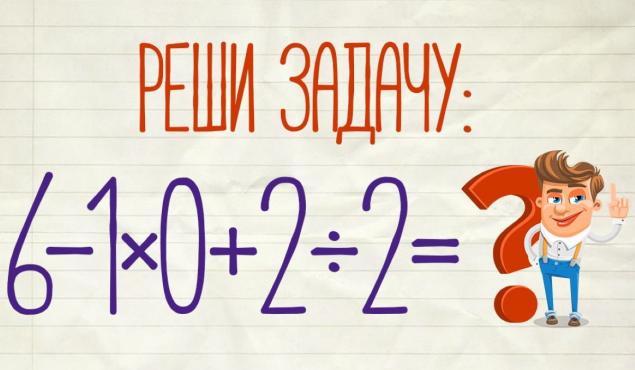Un ejemplo matemático para el efecto de la nostalgia dulce para las lecciones escolares

A los adultos les gusta fingir que saben todo. Pero si un niño pide ayuda con las lecciones, es más probable que reciba una negativa que una ayuda razonable. Por supuesto, esos tíos y tías que lo hicieron bien en la escuela, por supuesto, decidirán cualquier cosa. rompecabezas. ¿Cuántos? Sugerimos comprobarlo.

La edición de hoy. "Site" Ofrece dos problemas completamente diferentes, pero extremadamente interesantes que serán resueltos sólo por aquellos que siempre han sido amigos de las matemáticas. Una buena manera de probarse y averiguar si el cerebro está en buena forma, y si es capaz de resolver problemas de truco.



Puzzles matemáticos Condiciones y preguntas

1. Este parece ser simple Esto causó mucha discusión en Internet. Esto es porque diferentes lectores tienen respuestas diferentes. Algunos creen que la respuesta correcta es 5. Otros argumentaron que al final debería ser una unidad. Otros insistían en que 7 era el resultado correcto. ¿Quién tiene razón? ¿O la respuesta es completamente diferente?
   
   
   
   
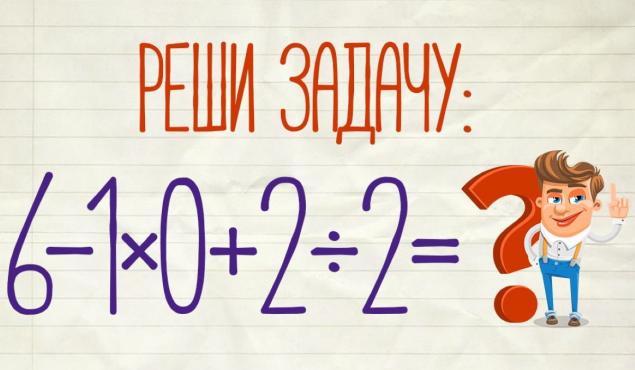
2. Si era posible entender fácilmente la primera tarea, entonces ofrecemos un problema donde usted necesita encender la lógica y pensar cuidadosamente. Se dice que una vez un caballero fue capturado por el sultán Saladin. El gobernador dijo que liberaría al prisionero y a su caballo si recibió un rescate masivo de 30.000 monedas de oro. El caballero no tenía dinero ni parientes ricos, así que decidió engañar. Oh poderoso Saladino, no me das esperanza. En mi patria, cada prisionero inteligente tiene la oportunidad de ser libre. Le están ofreciendo un rompecabezas. Si decide - se hace libre, si no decide - la cantidad de rescate se duplica, dijo el guerrero peculiar.
   
   A Saladin le encantaban los rompecabezas, así que le gustaba la oferta del prisionero.
   
   Está bien, déjalo así. Aquí está tu problema. Mañana por la mañana se le dará doce monedas de aspecto idéntico y una escala simple sin pesos. Una moneda será falsa. Pero nadie sabe si es más ligero o más pesado que otros. Tendrás tres pesas para determinar el falso. Si no puedes hacerlo, es malo para ti.
   
   ¿Cómo encontrar una moneda falsa entre 12 monedas en 3 pesas? ¿Es posible hacer eso?
   
   
   
   
   
   

Respuestas a los rompecabezas

1. Para resolver este ejemplo, necesitamos recordar la regla de la escuela que primero realizamos la multiplicación y división, y sólo entonces la adición y resta. Si es así, nuestro ejemplo tomará el siguiente formulario: 6 – 1 * 0 + 2 / 2 = 6 – 0 + 1 = 7.
   
   
2. El segundo problema llevará más tiempo resolver. Complicar es que no sabemos por condición que moneda es más pesada: falsa o real. No se sabe si el caballero logró encontrar una respuesta antes de la mañana para salir. Intentemos hacerlo por él.
   
   
   
   En primer lugar, dividir las monedas en 3 montones iguales de 4 monedas. Pesaremos los dos primeros lotes de monedas. Si son iguales en pesoAsí que tenemos suerte, y la moneda falsa está en la tercera pila.
   
   Luego pesa dos monedas reales (cualquier de la primera y segunda lote) y dos monedas de la última pila, donde había una falsa. Si las escalas nuevamente muestran la igualdad, entonces la moneda falsa es una de las dos restantes (de las que no tocamos).
   
   Por lo tanto, en el tercer paso, pesamos una de las monedas reales que ya conocemos de cualquiera de los dos restantes. Si la igualdad es otra vez, entonces la moneda falsa es la que no hemos tocado. Si no hay igualdad, entonces también se encuentra la falsificación. Al mismo tiempo, descubriremos si es más pesado que el original o más ligero.
   
   Si la desigualdad en el segundo peso, el par con el falso encontrado. Encontrar una moneda falsa para el tercer peso de nuevo no será difícil.
   
   
   
   
   
   Si en el primer pesaje Un grupo era más pesado, así que había una moneda falsa en los primeros ocho. Tal vez en este caso será mejor numerar todas las monedas: el primer montón (heavy) - 1,2,3,4; el segundo (light) - 5,6,7,8; el tercero (real) - 9,10,11,12.
   
   El segundo paso es pesar las monedas 1.9,10,11 y 2.3,4,5. Si la igualdad es falsa 6.7 ó 8. Al mismo tiempo, después del primer peso, ya aprendimos que el segundo lote es más fácil. Así que el falso es más ligero que el original. Así que pesamos 6 y 7. Cuanto más fácil es la falsificación. Si la moneda es igual, la moneda falsa es 8.
   
   Si, después del segundo paso, vimos que el grupo 1.9,10,11 es más pesado que el grupo 2.3,4,5, entonces el grupo falso es uno (más pesado) o 5 (más ligero). Es suficiente para pesar, decir, 1 y cualquier moneda real. Si uno es más pesado, es falso. Si la igualdad, entonces el falso es 5.
   
   Si el grupo es 2.3,4,5, significa que la moneda falsificada es más pesada, y es entre 2.3,4. En este caso, pesamos, por ejemplo, 2 y 3. Es más pesado, es falso. Si la moneda es igual, entonces la moneda bajo la condición número 4 será falsa.
   
   
   
   
   
   

¡Vaya! El último desafío no fue fácil. Por supuesto, sería posible simplificarlo cambiando las condiciones originales, pero ¿sería justo? Espero que el caballero también logró resolverlo, porque claramente tenía más motivación. ¿O tal vez hay una manera más fácil de encontrar?