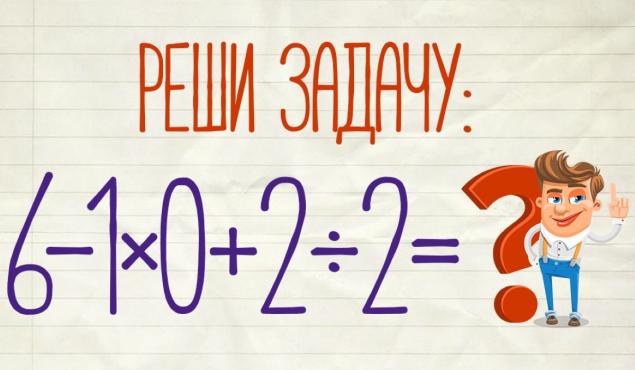A mathematical example for the effect of sweet nostalgia for school lessons

Adults like to pretend they know everything. But if a child asks for help with lessons, he is more likely to receive a refusal than reasonable help. Of course, those uncles and aunts who did well in school, for sure, will decide anything. puzzles. But how many? We suggest checking.

Today's edition. "Site" It offers two completely different, but extremely interesting problems that will be solved only by those who have always been friends with mathematics. A good way to test yourself and find out whether the brain is in good shape, and whether it is able to solve trick problems.



Mathematical puzzles Conditions and questions

1. This one seems to be simple It caused a lot of discussion on the Internet. This is because different readers have different answers. Some believe that the correct answer is 5. Others argued that in the end it should be a unit. Still others insisted that 7 was the right result. Who's right? Or is the answer completely different?
   
   
   
   
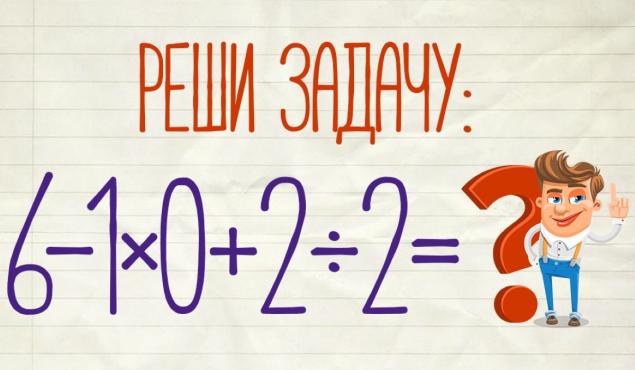
2. If it was possible to easily understand the first task, then we offer a problem where you need to turn on logic and think carefully. It is said that once upon a time a knight was captured by Sultan Saladin. The governor said he would release the prisoner and his horse if he received a massive ransom of 30,000 gold coins. The knight had neither money nor rich relatives, so he decided to cheat. “O mighty Saladin, you give me no hope. In my homeland, every smart prisoner is given a chance to be free. He's being offered a puzzle. If he decides - becomes free, if he does not decide - the amount of ransom is doubled, the quirky warrior said.
   
   Saladin loved puzzles, so he liked the prisoner's offer.
   
   “Okay, let it be so. Here's your problem. Tomorrow morning you will be given twelve identical-looking coins and a simple scale without weights. One coin will be fake. But no one knows if it is lighter or heavier than others. You'll have three weigh-ins to determine the fake. If you can't do it, it's bad for you.
   
   How to find a fake coin among 12 coins in 3 weighings? Is it even possible to do that?
   
   
   
   
   
   

Answers to puzzles

1. To solve this example, we need to remember the school rule that we first perform multiplication and division, and only then addition and subtraction. If so, our example will take the following form: 6 – 1 * 0 + 2 / 2 = 6 – 0 + 1 = 7.
   
   
2. The second problem will take longer to solve. Complicating it is that we do not know by condition which coin is heavier: fake or real. It is not known whether the knight managed to find an answer before the morning to get out. Let's try to do it for him.
   
   
   
   First of all, divide the coins into 3 equal heaps of 4 coins. We will weigh the first two batches of coins. If they're equal in weightSo we're lucky, and the fake coin is in the third pile.
   
   Then weigh any two real coins (any of the first and second batch) and two coins from the last pile, where there was one fake. If the scales again show equality, then the fake coin is one of the remaining two (of the ones we didn't touch).
   
   Therefore, in the third step, we weigh one of the real coins we already know from either of the remaining two. If equality is again, then the fake coin is the one we haven't touched. If there is no equality, then the fake is also found. At the same time, we will find out whether it is heavier than the original or lighter.
   
   If the inequality in the second weighing, the pair with the fake found. Finding a fake coin for the third weighing again will not be difficult.
   
   
   
   
   
   If at the first weighing One group was heavier, so there was a fake coin in the first eight. Perhaps in this case it will be better to number all coins: the first pile (heavy) - 1,2,3,4; the second (light) - 5,6,7,8; the third (real) - 9,10,11,12.
   
   The second step is to weigh the coins 1.9,10,11 and 2.3,4,5. If the equality is a false 6.7 or 8. At the same time, after the first weighing, we already learned that the second batch is easier. So the fake is lighter than the original. So we weigh 6 and 7. How much easier is the fake. If the coin is equal, the fake coin is 8.
   
   If, after the second step, we saw that the group 1.9,10,11 is heavier than the group 2.3,4,5, then the false group is either 1 (heavier) or 5 (lighter). It is enough to weigh, say, 1 and any real coin. If 1 is heavier, it's fake. If equality, then fake is 5.
   
   If the group is 2.3,4,5, it means that the counterfeit coin is heavier, and it is among 2.3,4. In this case, we weigh, for example, 2 and 3. It's heavier, it's fake. If the coin is equal, then the coin under the condition number 4 will be false.
   
   
   
   
   
   

Whew! The last challenge was not easy. Of course, it would be possible to simplify it by changing the original conditions, but would it be fair? I hope the knight also managed to solve it, because he clearly had more motivation. Or maybe there’s an easier way he found?