252
An insidious mathematical example that has two solutions
Hey, everybody! Who at school loved math? Despite the fact that it is difficult for many, mathematics is a very interesting science. In this article, we will discuss an interesting mathematical double-solution.
Example with two solutions
To solve this problem, you need to go beyond the usual mathematical actions that are studied in high school. We advise you to pay attention to different options for multiplication - this will help you get closer to the answer. In addition, this equation may seem very simple at first glance, but in fact it is a little tricky. Well, let's take a closer look at this equation.

How much did you do? Do not rush to answer because mathematics loves accuracy. Give yourself some time to think about the answer.

Most interestingly, this unique equation has two solutions. Some make 120 and others make 5! How is that even possible? However, mathematics is full of its secrets and hidden corners. We will try to understand why this is happening. By the way, how much did you end up with? If you can’t solve the problem, don’t worry, half of our editorial staff failed. Not everyone learned math so well in school.
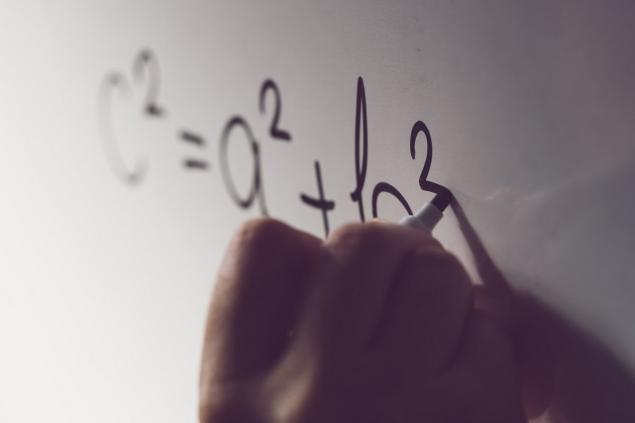
The answer is one small detail: the answer is not 5, but 5! The exclamation point after the five is factorial. This means that: 5! = 5 * 4 * 3 * 2 * 1 = 120. This post may seem too confusing. We'll dig deeper.

The factorial 1 (units) is equal to one and the factorial 2 (two) is equal to two. That is, 2! = 1 * 2 = 2. We go further: the factorial 3 (three) equals six - 3! = 1 * 2 * 3 = 6. The factorial 4 (four) is twenty-four: 4! = 1 * 2 * 3 * 4 = 24. Similarly, the factorial 5 is one hundred and twenty: 5! = 1 * 2 * 3 * 4 * 5 = 120. I think it makes sense that the following numbers multiply in the same way.

This task is not easy, but with a trick. Someone was able to solve it the first time, someone had to think a little about the answer. Ask your friends to solve this problem with two solutions. I hope they enjoy this problem. Good luck!
Example with two solutions

To solve this problem, you need to go beyond the usual mathematical actions that are studied in high school. We advise you to pay attention to different options for multiplication - this will help you get closer to the answer. In addition, this equation may seem very simple at first glance, but in fact it is a little tricky. Well, let's take a closer look at this equation.

How much did you do? Do not rush to answer because mathematics loves accuracy. Give yourself some time to think about the answer.

Most interestingly, this unique equation has two solutions. Some make 120 and others make 5! How is that even possible? However, mathematics is full of its secrets and hidden corners. We will try to understand why this is happening. By the way, how much did you end up with? If you can’t solve the problem, don’t worry, half of our editorial staff failed. Not everyone learned math so well in school.
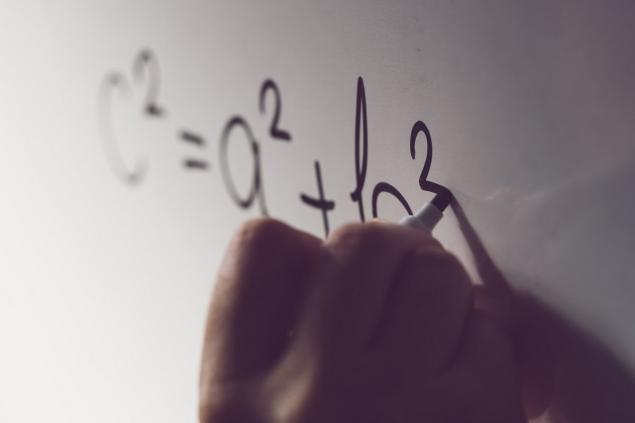
The answer is one small detail: the answer is not 5, but 5! The exclamation point after the five is factorial. This means that: 5! = 5 * 4 * 3 * 2 * 1 = 120. This post may seem too confusing. We'll dig deeper.

The factorial 1 (units) is equal to one and the factorial 2 (two) is equal to two. That is, 2! = 1 * 2 = 2. We go further: the factorial 3 (three) equals six - 3! = 1 * 2 * 3 = 6. The factorial 4 (four) is twenty-four: 4! = 1 * 2 * 3 * 4 = 24. Similarly, the factorial 5 is one hundred and twenty: 5! = 1 * 2 * 3 * 4 * 5 = 120. I think it makes sense that the following numbers multiply in the same way.

This task is not easy, but with a trick. Someone was able to solve it the first time, someone had to think a little about the answer. Ask your friends to solve this problem with two solutions. I hope they enjoy this problem. Good luck!
What French women do not allow themselves and their daughters after thirty
In what chest is your store of happiness hidden for February?