Вчені винайшли нові способи вирізати піцу

Габаритний зображення



Математика з університету Ліверпуля в своїй новій роботі опублікувала кілька раніше невідомих способів розділяти диск на рівні частини. Ця робота належить до розділу геометрії, яка вивчає так звані паркети - тротуар з полігонами без пробілів і перекриття. Робота надихнула пошуком способів вирізати піцу, процедури, які більшість нас знайомі.

При бліці площини з геометричними формами (талії), можна встановити і вирішувати різні завдання. Одним з найцікавіших завдань є використання моногрудної плитки. У цьому випадку всі плити мають однакову форму, а точніше, плутають. Це означає, що будь-які дві плитки можна поєднувати за допомогою рухів, обертань або дзеркального відображення.

Набір форм плитки, що використовується для заміни площини називається протопілами. Цікаво, що не існує математичного методу, який дозволяє говорити заздалегідь, чи можна замінити площину за допомогою наданих протоплітів. Наприклад, відомо, що з наступних 24 гептамонів (фігури, що складаються з семи рівнокутних трикутників) тільки один не підходить для моноглодрального тротуару площини. Але що?



У цьому випадку він V-подібний. Але доказ цього є досить непривабливим завданням.

Однак, Ліверпульові математики, замість цілої площини, згорнуті себе на диск і почали шукати монохедральні протопліти, придатні для розділення диска. Один варіант такої виступи відомий всім. З стандартним методом ріжучої піци ділиться на рівні скибочки трикутної форми, верхівки якого конвержуть в центрі диска. Вчені вирішили відповісти на питання – є такі розділи диска на рівні фігури, в яких не всі ці цифри торкаються центру диска?

Що ж ви можете вирізати піцу в рівних частинах, щоб порадувати тих, хто любить більше наповнення і тих, хто любить більше скоринки? Вимкніть ви можете. Крім того, один варіант такого різання був відомий довгий час, і знаходиться на логотипі спільноти Пенсільванського державного університету, який організовує математичні семінари для студентів:



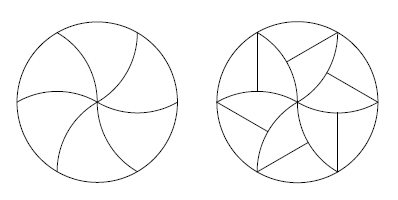
Фігурні лоби можна розділити навпіл, а всі деталі будуть плутати, тільки половина з них доторкнутися до центру.

Математики розвивали цю ідею і запропонували власні способи поділу диска в майже нескінченну кількість рівних частин.

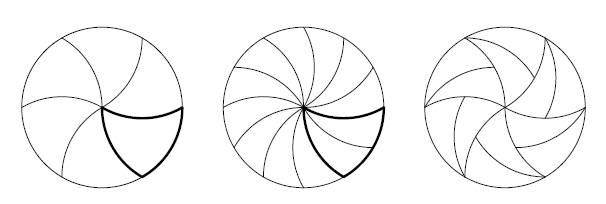р.





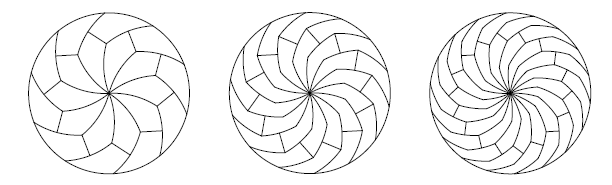
Як часто справа в математики, можливості застосування ідей роботи на практиці не зовсім очевидні – крім того, що піцерія використовує на замовлення піцерію різання як конкурентну перевагу. Але з іншого боку, не можна передбачити, як буде корисно математичне відкриття.

Джерело: geektimes.ru/post/269082/