科学家们发明了切割比萨饼的新途径

href="http://phys.org/news/2016-01-mathematical-recipe-slicing-pizza.html">出版了几先前未知的方式分区从利物浦大学数学的他的新工作паркеты - 平铺多边形面没有空白和重叠。在工作​​中激发了科学家寻找方法来削减比萨 - 我们大多数人都熟悉的过程

当平铺平面几何图形（砖）可以设置和解决不同的问题。其中最有趣的问题 - 使用monoedricheskih瓷砖。在这种情况下，所有的瓷砖具有相同的形状，或更精确地说，是一致的。这意味着，任何两个区域可以用平移，旋转或镜像进行组合。

设置用于更换飞机的砖的形式，称为protoplitkami。有趣的是，没有任何数学方法事先说是否有可能使用指定protoplitok替换的平面。例如，已知的是从<一个href="http://www.math.cornell.edu/~mec/2008-2009/KathrynLindsey/PROJECT/Page2.htm">следующих 24 geptamondov （形状7等边三角形组成）中，只有一个是不适合贴砖monoedricheskogo平面。但究竟是什么？



在这种情况下 - V形。但证明了这一点 - 一个相当简单的任务

然而，利物浦的数学，而不是整个盘面的限制，寻求适合划分磁盘monoedricheskih protoplitok。一个版本大家都知道这样的protoplitki的。在切割比萨饼的标准方法，它被分成相等片三角形状，顶部其中会聚在中心。科学家还决定回答的问题 - 是否有分割磁盘划分为相等的部分，其中并非所有这些数字涉及到中心磁盘？

也就是说，是否有可能削减比萨分成相等的部分，以取悦无论是谁喜欢多一点的填充，并为那些喜欢谁多一点褐色的？原来，你可以。此外，一个这样的切割实施方案是已知的很长一段时间，而且位于标志社区，宾夕法尼亚大学的，举办研讨会数学学生：



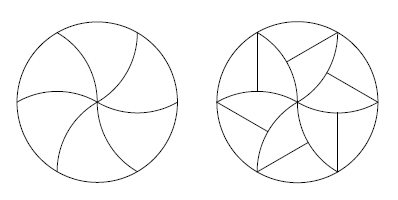
该形切片可以一分为二，并且所有部分都只有一半的人都会接触到中心取得一致。

数学家们开发了这个想法，并提供了驱动器划分为相等的部分几乎无限数量的方式。







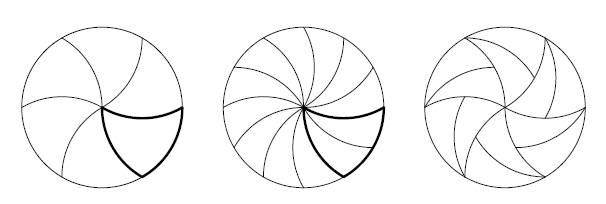
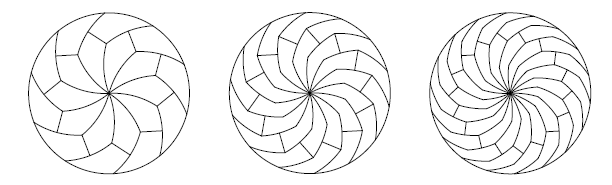
由于经常发生在数学，应用观念的可能性，在实践中并不完全清楚 - 也许，使用非标刀具比萨店比萨的竞争优势。另一方面，来预测所述数学发现将在未来是有用的，它也不可能。

资料来源： geektimes.ru/post/269082/