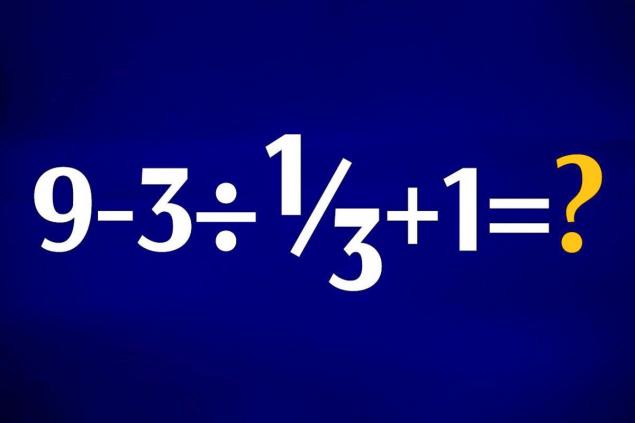Un ejemplo elemental en torno al cual los ciudadanos no se cansan de discutir

Los maestros lucharon durante mucho tiempo para formar un conocimiento matemático confiable. Lamentablemente, la mayoría de ellos desapareció inmediatamente después de los exámenes. Por lo tanto, simples tareas infantiles y desconcertante experiencia de vida sabia adultos. ¿No? Vea si tiene el conocimiento para manejar nuestros ejemplos.



Peels Mathematical Knowledge

1. ¿A quién no le gusta una buena conversación en línea? No importa, la batalla es entre partidarios de kvass y kefir o un intento de determinar el color de un vestido misterioso. Sería una razón para hablar y romper los argumentos del lado opuesto al polvo.
   
   
   
   Y este ejemplo también ofrece una oportunidad así. En Facebook, 16.000 personas ya han comentado. Para los más impacientes de ellos, la respuesta estaba lista en un segundo: por supuesto, 1! Pero, como dicen, date prisa y haz reír a la gente.
   
   
2. Este simple ejemplo se hizo famoso en Japón y luego ganó popularidad en todo el mundo gracias a las redes sociales. Los autores señalan que en los años 80, el 90% de los estudiantes podrían resolverlo sin problemas. Hoy, menos de la mitad.
   
   
   
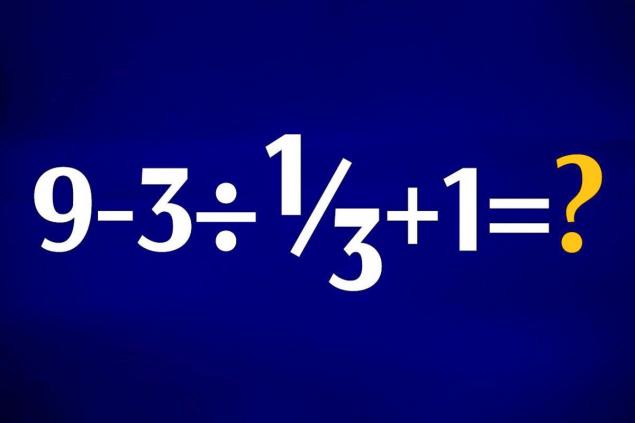
3. Algunos dirán que este ejemplo es demasiado simple. Pero puedo asegurarle que la asombrosa abundancia de respuestas en los comentarios sugiere claramente lo contrario.
   
   
   

Respuestas.

1. Como puedes ver, tendrás que deshacerte del orden olvidado de las acciones matemáticas. Todos le enseñamos en la escuela primaria. Y hoy, muchas personas saben gracias a la regla mnemónica de PEMDAS: corchetes, grado, multiplicación, división, adición, resta.
   
   
   
   “Eso es lo que pensamos”, desafiaron los autores de “1”. Y explican: "Primera acción entre corchetes, luego multiplicación y última división". Se sabe que el diablo está en los detalles. Y este ejemplo no es una excepción.
   
   La división y la multiplicación tienen la misma prioridad. Entonces tienes que hacerlo. izquierda. De esto obtenemos 6: 2 (1 + 2) = 6: 2 * 3 = 3 * 3 = 3 = 9..
   
   
2. El problema principal aquí es que muchos simplemente no recuerdan cómo dividir un número por fracción. Pero esta operación matemática será la primera. Primero tienes que dividir y multiplicar, y sólo entonces añadir y restar.
   
   
   
   Dividir un número por una fracción es como multiplicarlo por la misma fracción, habiendo cambiado previamente el numerador y los lugares denominadores. Entonces nuestro ejemplo obtiene una forma más comprensible: 9 - 3 * 3 + 1 = 9 - 9 + 1 = 1a.
   
   

Como ya hemos dicho, las acciones aritméticas se realizan a su vez de izquierda a derecha. Al mismo tiempo, en primer lugar, las acciones se realizan entre corchetes, luego división y multiplicación, y sólo entonces adición y resta. En palabras, simples, pero en la práctica, surgen problemas. ¿Dónde obtendrían respuestas los lectores 0 y 3?



Según las reglas, primero realizamos acciones entre corchetes. 5 - 4 + 1 = 2. Luego 18/3 * (5 - 4 + 1) = 18/3 * 2. Y aquí se encuentra otra roca submarina insidiosa. En teoría, la división puede ser denotada por un colon (:), un obelus (÷), un slash (/) o un signo fraccional (-).

Con la entrada de la computadora, el signo de la fracción es a menudo reemplazado por un corte para la simplicidad. Por lo tanto, muchas personas erróneamente perciben la expresión “18 / 3 * 2” como una fracción, donde en el numerador 18, y en el denominador 3 * 2. Y esto sería cierto si nuestro ejemplo tuviera la forma 18 / (3 * (5 - 4 + 1)). Pero no hay paréntesis detrás del signo de división, lo que significa que no puede ser percibido como un rasgo fraccional. De ahí 18 / 3 * 2 = 6 * 2 = 12..



Espero que haya disfrutado tomando ejemplos como este. No te olvides de escribir las respuestas que tienes. ¿Realmente cometimos un error en alguna parte?