1750
"¿Cuál es la prueba?": Perspectivas de la ciencia de la computación teórica
Ciencias de la Computación Teórica - una de las áreas de aprendizaje en el departamento Académico href="http://mit.spbau.ru">. A menudo nos preguntan cuál es la ciencia de la computación teórica. Teórica Ciencias de la Computación - un área de investigación en rápido crecimiento, que incluye tanto áreas fundamentales: algoritmos, complejidad computacional, criptografía, teoría de la información, teoría de la codificación, la teoría de juegos algorítmica, y más aplicado: la inteligencia artificial, aprendizaje automático, la semántica de los lenguajes de programación, verificación, automática demostración de teoremas, y más. En este artículo se dedicará a la revisión de sólo una pequeña parcela, es decir, hablan de un enfoque inusual al concepto de pruebas que considera la ciencia de la computación teórica.

Para explicar lo que se discutirá tipo de pruebas, considere un ejemplo: hay un programa de ordenador cuyos autores afirman que el programa está haciendo algo específico (ejemplos específicos serán más adelante). El programa puede funcionar y obtener la respuesta. Y ¿cómo puede asegurarse de que el programa hace lo que se supone que debe hacer? Sería bueno si, además de la respuesta al programa presentado pruebas de que la respuesta es correcta.
Consideremos un ejemplo concreto: queremos tener un programa que en un grafo bipartito es un juego de tamaño máximo junto con el comprobante de su máximo.
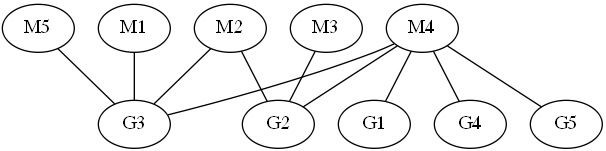
Recordemos que un gráfico bipartito es si sus vértices se pueden colorear en dos colores de modo que los bordes de la gráfica se conectan los vértices de diferentes colores. Coincidente en un gráfico es un conjunto de aristas, no hay dos de ellos tienen un fin común. Conjunto de vértices se llama una cubierta si cada borde de la gráfica tiene al menos un extremo en este conjunto. Koenig teorema afirma que un grafo bipartito de tamaño máximo coincidente coincide con el tamaño del conjunto de spanning mínimo. Por lo tanto, para demostrar que una coincidencia máxima, se puede presentar, cubriendo conjunto cuyo tamaño coincide con el tamaño del juego. De hecho, se cubre el conjunto será mínimo, ya que se requiere cada conjunto que cubre para cubrir al menos un extremo de cada borde de la coincidencia. Por ejemplo, el gráfico de la figura correspondiente (M1, G3), (M2, G2), (M4, G1) se maximizará ya que no cubre una pluralidad de tamaño 3, que consiste en G2, G3, y M4. Tenga en cuenta que el cheque es una prueba es mucho más fácil que para calcular un acoplamiento máximo, suficientes para comprobar que el tamaño de matchings coincide con el tamaño de la cubierta de la serie y compruebe que todos los bordes están cubiertos.
Considere otro ejemplo, digamos que tenemos un programa que comprueba el sistema de no-estrictos desigualdades lineales con coeficientes racionales sobre la articulación (recordemos que el sistema de desigualdades se dice que es consistente si podemos encontrar los valores de las variables que todas las desigualdades están satisfechos).
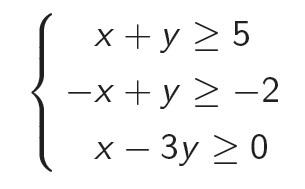
¿Cómo podemos demostrar la exactitud del resultado? Si el sistema es consistente, entonces la prueba de la consistencia puede ser una solución del sistema (es fácil de demostrar que si un sistema de este tipo tiene una solución, entonces hay una solución racional, es decir, se puede escribir). Pero, ¿cómo demostrar que el sistema es inconsistente? Resulta que esto se puede hacer mediante el uso de Farkas Lema, que establece que si el sistema es no-estrictos desigualdades lineales es inconsistente, entonces usted puede agregar estas desigualdades con coeficientes no negativos y obtener la desigualdad contradictoria 0≥1. Por ejemplo, el sistema en la figura es inconsistente, y si añadimos la primera ecuación por un factor de 1, el segundo por un factor de 2, y el tercero por un factor de 1, se obtiene 0≥1. La prueba de la inconsistencia es sólo un conjunto de coeficientes no negativos.
En este artículo, hablaremos acerca de si o no las pruebas o evidencias de prueba no siempre es más fácil que las tareas de decisión independientes. (En el ejemplo de la coincidencia máxima, no hemos demostrado que no hay ningún algoritmo para resolver el problema en el mismo tiempo, el tiempo que tarda la verificación de la prueba.) Si no limitamos el tamaño de la evidencia, parece que es necesaria la evidencia, y si requiere que las pruebas eran correcta, entonces la cuestión de la utilidad de la prueba equivalente al descubrimiento importante de la cuestión de la igualdad de las clases P y NP. A continuación hablaremos de pruebas interactivas (prueba en el diálogo). Se discute la evidencia criptográfica que no divulga la información innecesaria, excepto la lealtad demuestra la afirmación. Y para terminar la discusión pruebas verificables probabilísticamente y teorema PCP-famoso, que se utiliza para demostrar la dificultad de aproximación de problemas de optimización.
En este artículo, no nos ocupamos de demostración de teoremas automática y prueba de la corrección de los programas, aunque estos temas también son muy interesantes.
¿Necesitas una prueba? H4>
Pruebas cortas h4>

Para explicar lo que se discutirá tipo de pruebas, considere un ejemplo: hay un programa de ordenador cuyos autores afirman que el programa está haciendo algo específico (ejemplos específicos serán más adelante). El programa puede funcionar y obtener la respuesta. Y ¿cómo puede asegurarse de que el programa hace lo que se supone que debe hacer? Sería bueno si, además de la respuesta al programa presentado pruebas de que la respuesta es correcta.
Consideremos un ejemplo concreto: queremos tener un programa que en un grafo bipartito es un juego de tamaño máximo junto con el comprobante de su máximo.

Recordemos que un gráfico bipartito es si sus vértices se pueden colorear en dos colores de modo que los bordes de la gráfica se conectan los vértices de diferentes colores. Coincidente en un gráfico es un conjunto de aristas, no hay dos de ellos tienen un fin común. Conjunto de vértices se llama una cubierta si cada borde de la gráfica tiene al menos un extremo en este conjunto. Koenig teorema afirma que un grafo bipartito de tamaño máximo coincidente coincide con el tamaño del conjunto de spanning mínimo. Por lo tanto, para demostrar que una coincidencia máxima, se puede presentar, cubriendo conjunto cuyo tamaño coincide con el tamaño del juego. De hecho, se cubre el conjunto será mínimo, ya que se requiere cada conjunto que cubre para cubrir al menos un extremo de cada borde de la coincidencia. Por ejemplo, el gráfico de la figura correspondiente (M1, G3), (M2, G2), (M4, G1) se maximizará ya que no cubre una pluralidad de tamaño 3, que consiste en G2, G3, y M4. Tenga en cuenta que el cheque es una prueba es mucho más fácil que para calcular un acoplamiento máximo, suficientes para comprobar que el tamaño de matchings coincide con el tamaño de la cubierta de la serie y compruebe que todos los bordes están cubiertos.
Considere otro ejemplo, digamos que tenemos un programa que comprueba el sistema de no-estrictos desigualdades lineales con coeficientes racionales sobre la articulación (recordemos que el sistema de desigualdades se dice que es consistente si podemos encontrar los valores de las variables que todas las desigualdades están satisfechos).
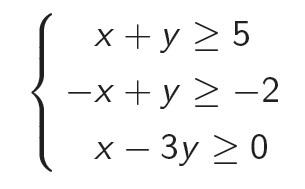
¿Cómo podemos demostrar la exactitud del resultado? Si el sistema es consistente, entonces la prueba de la consistencia puede ser una solución del sistema (es fácil de demostrar que si un sistema de este tipo tiene una solución, entonces hay una solución racional, es decir, se puede escribir). Pero, ¿cómo demostrar que el sistema es inconsistente? Resulta que esto se puede hacer mediante el uso de Farkas Lema, que establece que si el sistema es no-estrictos desigualdades lineales es inconsistente, entonces usted puede agregar estas desigualdades con coeficientes no negativos y obtener la desigualdad contradictoria 0≥1. Por ejemplo, el sistema en la figura es inconsistente, y si añadimos la primera ecuación por un factor de 1, el segundo por un factor de 2, y el tercero por un factor de 1, se obtiene 0≥1. La prueba de la inconsistencia es sólo un conjunto de coeficientes no negativos.
En este artículo, hablaremos acerca de si o no las pruebas o evidencias de prueba no siempre es más fácil que las tareas de decisión independientes. (En el ejemplo de la coincidencia máxima, no hemos demostrado que no hay ningún algoritmo para resolver el problema en el mismo tiempo, el tiempo que tarda la verificación de la prueba.) Si no limitamos el tamaño de la evidencia, parece que es necesaria la evidencia, y si requiere que las pruebas eran correcta, entonces la cuestión de la utilidad de la prueba equivalente al descubrimiento importante de la cuestión de la igualdad de las clases P y NP. A continuación hablaremos de pruebas interactivas (prueba en el diálogo). Se discute la evidencia criptográfica que no divulga la información innecesaria, excepto la lealtad demuestra la afirmación. Y para terminar la discusión pruebas verificables probabilísticamente y teorema PCP-famoso, que se utiliza para demostrar la dificultad de aproximación de problemas de optimización.
En este artículo, no nos ocupamos de demostración de teoremas automática y prueba de la corrección de los programas, aunque estos temas también son muy interesantes.
¿Necesitas una prueba? H4>
El lenguaje es el conjunto de las cadenas sobre algún alfabeto finito. En ciencias de la computación teórica que se considera por lo general pruebas de las declaraciones de la forma x∈L, donde L - lenguaje, yx - alguna cadena. Las afirmaciones de este tipo de teoremas matemáticos generalizan, como cualquier teorema matemático afirma que una declaración grabada en un lenguaje formal, pertenece al conjunto de enunciados verdaderos.
Sistema de prueba para un lenguaje L es un algoritmo A (x, w), que toma como entrada dos líneas: x y w y comprueba que una cadena w es una prueba de la afiliación x∈L. Desde el sistema de prueba requiere dos propiedades: corrección y exhaustividad. Corrección establece que si para algunas cadenas x y w algoritmo A (x, w) las salidas 1, entonces x∈L. Estados de integridad que por cada no existe cadena x∈L w, el algoritmo A (x, w) SALIDAS 1.
Idiomas para los que existen evidencias de un sistema, llamado idiomas enumerables. Si usted se enfrenta con un lenguaje enumerable definición diferente, como un ejercicio, demostrar su equivalencia.
Idioma L es soluble si hay un algoritmo B, que x∈L algoritmo (x) las salidas 1, mientras que x∉L da 0. B Cualquier lenguaje es el sistema de prueba decidible en el que la prueba está vacía. Una pregunta natural, ya sea necesariamente, para cualquier idioma para el que no hay pruebas de un sistema, y no hay un algoritmo de decisión. La respuesta a esta pregunta se conoce, hay lenguas para las que existen pruebas del sistema, pero para los que no hay algoritmo para decidir. Vamos con una especie de ejemplo de un lenguaje tal no es difícil, más difícil que llegar a un ejemplo natural. Considere el lenguaje que consiste de polinomios con coeficientes enteros de las muchas variables que se desvanecen al menos en algunas variables enteras. Sistema de prueba de este lenguaje se construye simplemente, la prueba será de variables enteras, en el que el polinomio se desvanece. DPRM-teorema (llamado por los autores: Davis, Putnam, Robinson y Matiyaesevich) sostiene que esta lengua no tiene solución, es decir, no hay ningún algoritmo que comprueba si un polinomio se señala a cero en puntos enteros. El último paso en la demostración de este teorema por el académico V. Matijasevic y este teorema da una respuesta negativa a la décimo problema de Hilbert.
Pruebas cortas h4>
Si bien no imponemos ninguna restricción sobre el algoritmo que comprueba la prueba y el tamaño de la prueba. ¿Habrá una prueba útil de la exactitud de los resultados de algunos programas si el tiempo necesario para verificar la evidencia más de la ejecución del programa? Parece que tales pruebas no tiene sentido, por lo que requiere que el algoritmo A (x, w) en la definición de pruebas funcionaría polinomio en x de la longitud y la longitud de tiempo w prueba, como sistema de prueba será llamado eficaz.

Decimos que un lenguaje L pertenece a la clase NP, si tiene un sistema efectivo de pruebas y un polinomio p, tal que para existe ninguna prueba x∈L longitud accesorios x∈L no mayor que p (| x |). El lenguaje L pertenece a la clase P, si existe un algoritmo de tiempo polinómico que verifica la identidad de la cadena de entrada en L. La clase P está contenido en la clase NP, ya que para cada lenguaje L en P, el algoritmo comprueba la identidad L, y él será un sistema de pruebas, si se supone hace caso omiso de la prueba. Por el momento no se sabe si hay lenguas en la clase NP, que no pertenecen a la clase P. La cuestión de Clases de complejidad P y NP está incluido en la lista de los siete problemas del milenio, compilado por el Instituto de la arcilla; para la solución de este problema se declara un premio de un millón de dólares. Muchos han oído hablar de la lista de tareas en relación con la prueba de milenio de la conjetura de Poincaré GY Perelman. La mayoría de los expertos creen que las clases P y NP no son los mismos.
Considere los ejemplos de lenguas de la clase NP:
- números compuestos lenguaje es en la clase NP. Para demostrar que el número n de compuesto suficiente para producir dos enteros A y B, que es mayor que uno y n = ab. Primos del idioma también se encuentra en la clase NP, pero es más difícil de probar. Sin embargo, en 2002, Kayal y Saxena demostraron que el lenguaje es simple (y, en consecuencia, el compuesto) de los números es en la clase P.
- Considere la GI idioma, que consiste en pares de grafos isomorfos. Creemos que los vértices de la gráfica están numeradas de 1 a N, cada
exactamente un borde conecta un par de vértices. Dos gráficos G 1 sub> (V 1 sub>, E 1 sub>) y G 2 sub> (V 2 sub>, E 2 sub>) se llaman isomorfos si los vértices de la primera gráfica se pueden numerar de manera que la primera gráfica es idéntica a la segunda gráfica. Esto significa que después de volver a numerar el primer conjunto de aristas del grafo coincide con el conjunto de bordes de la segunda gráfica. Idioma GI se encuentra en la clase NP, la prueba será de permutación gráficos isomorfo de los vértices de la primera gráfica, que define un isomorfismo. Se encuentra en si la clase GI lenguaje P, es una pregunta abierta. Considere también la lengua del INB, que consiste en pares de gráficos no isomorfos en el mismo número de vértices. Acerca idioma INB desconoce si él está en NP, ya que no está claro cómo brevemente prueban que dos gráficos son isomorfos.
- Considere la HamPath lenguaje, que consta de gráficos en los que hay un camino de Hamilton, es decir, de tal manera que exactamente una vez a través de cada vértice. Este lenguaje está en la clase de la PN, ya que como evidencia de las posibles maneras de utilizar la ruta de acceso local. Acerca de este idioma no se sabe si él estaba en una clase de P, pero se sabe que es NP-completo. Este último, en particular, significa que HamPath no está en P, si P ≠ NP. Suplemento HamPath idioma coincide con el conjunto de gráficos en los que hay un camino hamiltoniano. Se encuentra en si se desconoce la clase HamPath Además NP.
Pruebas interactivas h4>
Hasta ahora, la evidencia que hemos considerado que es muy similar a los EE.UU. habitual, es decir, la prueba - este es un texto que, aunque no está claro cómo inventar, pero es fácil de comprobar, hay un algoritmo que verifica la exactitud de la prueba. Eso es para llegar a la prueba es necesario tener ninguna habilidad especial, y verificar la prueba de todo el mundo puede. De hecho, no toda la evidencia de la matemática moderna tiene esta propiedad. En primer lugar, la evidencia no escribe en una forma fácil de comprobar automáticamente el lenguaje formal, y en segundo lugar, para comprender la evidencia en algunas áreas, lo necesario para pasar varios años estudiando esta área.
En los círculos matemáticos para alumnos a menudo se practica esta clase de formato: los niños que recibieron conjunto de tareas cuando el niño cree que él resolvió el problema, dijo el profesor de la decisión por vía oral. Y hay un diálogo entre el profesor y el alumno, quien convence al profesor o que el problema se resuelve o no convincente.
Consideremos el ejemplo de una prueba interactiva: hay un programa que resuelve el problema de isomorfismo de grafos. En el caso de que los gráficos son isomorfos, el programa puede demostrar la exactitud de su respuesta, teniendo permutación dada da un isomorfismo. Mostramos cómo el diálogo puede probar que los gráficos son isomorfos. Deje que los gráficos del programa se le preguntó por el usuario son isomorfos si G 0 sub> y G 1 sub> y recibió una respuesta que no son isomorfos. El usuario lanza una moneda (selecciona un elemento aleatorio i del conjunto {0, 1}), y selecciona una permutación aleatoria de un conjunto de n elementos (todas las permutaciones se consideran igualmente probable) σ. Y pide a los gráficos del programa son isomorfos si G 0 sub>, σ (G i sub>). Si i = 0, entonces se espera que el programa para responder que las gráficas son isomorfos, y si i = 1, entonces se espera que el programa que los gráficos no son isomorfos. Si el grafo G 0 sub> y G 1 sub> de hecho eran isomorfos, entonces el programa sin dificultad dar la respuesta correcta a esta pregunta. Y si G 0 sub> y G 1 sub> son isomorfos, entonces la gráfica de σ (G i sub>) es la misma probabilidad de ser una permutación de G 0 sub>, y la permutación G 1 sub>, por lo que el programa va a dar la respuesta esperada con una probabilidad mayor que 1/2. La probabilidad de error se puede reducir mediante la repetición de los algoritmo n veces y decidir que el algoritmo funciona correctamente si cada uno de los n carreras se les dio la respuesta correcta; la probabilidad de error en este caso no supera 1/2 n sup>.
En el ejemplo anterior, la única evidencia de que - se trata de un diálogo entre prueba (programa) y la inspección (por el usuario), lo que demuestra se puede arreglar muy difícil, y el verificador sólo puede hacer cosas sencillas (para producir un cálculo en tiempo polinomio). Si el artículo x∈L, demostrando que con probabilidad 1 debe convencer al examinador, y si x∉L, a continuación, el verificador debe aceptar esas pruebas con la probabilidad de no más de 1/10. El teorema de Shamir afirma que tales IP con diálogos cortos existe para todos los lenguajes L, para los que hay un algoritmo de reconocimiento de la memoria usando polinomio. En particular, podemos en tiempo polinomial para demostrar que la gráfica no tiene camino de Hamilton.
Cero-conocimiento a prueba h4>
El concepto de evidencia se encuentra no sólo en matemáticas y ciencias de la computación, sino también en el derecho. Por ejemplo, una persona acusada de un crimen, él puede probar que él no estaba en la escena del crimen, pero no quiere revelar dónde estaba en realidad (por ejemplo, podría ser un amante o quieres ocultar tu ubicación de la competencia). Alibi no es un delito, pero su lectura es muy indeseable. Resulta que es teóricamente posible para no probar con el fin de revelar demasiada información, que no sea la afirmación requerida.
Considere este ejemplo: algunas empresas escriben programas que resuelvan el problema de isomorfismo gráfico rápido, pero la versión gratuita de este programa sólo dice gráficos son isomorfos o no, dando una permutación cuando los gráficos son isomorfos. Para obtener una permutación, usted necesita comprar la versión de pago. Pero mientras tanto, los desarrolladores quieren que el usuario pueda asegurarse de que los gráficos de hecho isomorfo, pero que esta información no ayuda al usuario a encontrar el isomorfismo posee. Esto se puede hacer de la siguiente manera: si los gráficos G 0 sub> y G 1 sub> son isomorfos, entonces usted puede seleccionar un π permutación aleatoria y emite un grafo G 2 sub> = π ( G 1 sub>) y solicitará al usuario que decida isomorfismo de grafos que quiere conseguir el G 0 sub> y G 2 sub> y G 1 sub> y G 2 sub>. El programa responderá exactamente a una de estas consultas. Si el programa sabe que el isomorfismo, se puede responder fácilmente a su petición, si no es un isomorfismo, entonces por lo menos una de las opciones para la solicitud del usuario para emitir una respuesta. Y si el usuario seleccione la consulta al azar, entonces la probabilidad de que el isomorfismo entre las opciones seleccionables por el usuario está, no sea superior a 1/2. Error se puede reducir mediante la repetición de este proceso:. La elección de una nueva permutación y pide al usuario que seleccione una nueva opción
Resulta que para cada idioma en la clase NP bajo algún supuesto de cifrado que se puede construir una prueba de tales interactivo de pertenencia, que no va a dar ninguna información acerca de la prueba clásica de afiliación (que existe para cualquier idioma en la clase NP). Dicha suposición criptográfica - es la existencia de funciones unidireccionales, es decir, funciones que son fáciles de calcular, pero difícil de rechazar. Por ejemplo, muchos creen que la función que los dos números de n bits ofrece su producto es de un solo lado.
pruebas verificables probabilísticamente h4>
Deje que su profesor de matemáticas le da a los estudiantes la tarea, que él un cuaderno con la decisión de aprobación. Cualquier profesor de matemáticas de los sueños, así que usted puede comprobar la solución sin leerlo completamente. Opción para comprobar la solución sólo por las respuestas es malo, porque la respuesta puede darse por perdida o supongo, y también que no ayuda en las tareas en la evidencia, en la que las respuestas como tales o no.