1185
Bitcoin Minería veterano de IBM 1401 55 años
Inspirado por la publicación habrapolzovatelya mark_ablov « Mein Bitcoin través de lápiz y papel », se decidió que los lectores giktaym preguntándose qué otra locura de ideas capaces de darse cuenta de que el autor del post original -. Ken Shirriffu i>
¿Puedo utilizar el mainframe de IBM viene de los años 60 del siglo pasado Mein Bitcoins? Decidí probar esto, a primera vista, una idea loca. He implementado un algoritmo de hash Bitcoin en código ensamblador para el IBM 1401 y probado en la práctica mediante la ejecución de un modelo viable de esta antigua mainframe.

Tarjeta, que se calcula utilizando el SHA-256 hashes en el mainframe IBM marcó tarjeta 1401.Za impresión visible en la impresora, que muestra la entrada del algoritmo y el hash resultante i>
Al final resultó que, con la ayuda de la computadora puede ser principal, pero el proceso lleva tanto tiempo que ni siquiera el tiempo de vida del universo puede no ser suficiente para un bloque único éxito de la minería.
Mientras que el hardware moderno permite calcular hashes miles de millones por segundo, el equipo en 1401 pasa 80 segundos para calcular un solo hash. Rendimiento Progreso de las computadoras en la última década hay que describe claramente la Ley de Moore.
Sacador tarjetas, participaron en el experimento, así como la impresión SHA-256 impresora de línea se muestra en las fotos (la primera tarjeta es una belleza - que no era fácil de romper este patrón). Tenga en cuenta que la segunda línea termina con un grupo de ceros; Esto significa un hash éxito.
El principio del sistema de la minería Bitcoin
En los últimos años, la moneda electrónica Bitcoin (Bitcoin), que los usuarios de Internet pueden enviar uno al otro, es muy popular. Para comprender la esencia criptomoneda actual, el sistema de Bitcoin se puede representar en forma de un libro de registro en el que un registro de los propietarios de las monedas digitales (Bitcoin) y el número de monedas que él / ella tiene. Los compradores Bitcoin puede transmitir la moneda digital de uno al otro.
Cabe señalar que el sistema de Bitcoin descentralizada: no tiene un único servidor de regulación, lo que seguir el curso de la operación. En cambio, estamos distribuyendo los registros de una red distribuida de miles de ordenadores en Internet.
La dificultad radica en el hecho de que tal sistema de distribución debe asegurar de alguna manera que el consentimiento de todos los usuarios en los registros. Es decir los usuarios de buena fe deben confirmar la validez de una transacción, aprobarlo, a pesar de la posible presencia de estafadores y trabajando lentamente su red. La solución a este problema fue la llamada "minería". Aproximadamente cada 10 minutos durante la unidad de salida de la minería confirmaron la transacción, como resultado, se le considera ser confirmada oficialmente.
El proceso de la minería, basado en una criptografía robusta, es extremadamente difícil, por lo que nadie puede controlar exactamente qué transacciones son la minería. En particular, la idea clave de Bitcoin es que el resultado de complejas y difíciles de obtener, pero es fácil de comprobar. Esta es la llamada tecnología «prueba de trabajo» («prueba de trabajo»).
El proceso de bloque de la minería requiere una enorme cantidad de costos de computación. Sin embargo, después de que la unidad ha sido certificado, los usuarios se asoman red puede fácilmente verificar su validez. La complejidad de la minería evita el uso fraudulento de Bitcoin, y la facilidad de unidad de verificación permite a los usuarios tener la confianza en la validez de la transacción.
Un efecto secundario de la minería es la adición de nuevo sistema de Bitcoin. En la actualidad, cualquier persona que confirmó la unidad recibe un 25 generada Bitcoin (ahora el coste del número de monedas virtuales en términos monetarios tradicionales se trata de 6000. USD). Esta promoción alienta "mineros" que trabajar duro y gastar sus recursos en la minería. Dada la oportunidad disponible para llegar a 6 dólares XX. Estados Unidos cada 10 minutos, la minería representa una verdadera "mina de oro", animando a los usuarios a gastar sumas considerables en hardware para la minería.

impresora de líneas y de mainframe de IBM en 1401, se presenta en la exposición del Museo de Historia de la Computación (Computer History Museum). Este equipo está funcionando mi programa. La consola se encuentra en la parte superior izquierda. Panel rectangular Negro en el equipo es una bastidores "puerta" que se reclinan, permitiendo el acceso para el mantenimiento. I>
El proceso de extracción extremadamente difícil, pero el resultado es muy fácil de comprobar. El Bitcoin Minería utiliza función hash de criptografía, llamado SHA-256 doble. Porción Hash toma los datos de entrada y lo reduce a un valor hash más pequeña (en este caso 256 bits).
Un algoritmo de hash criptográfica no cederá el valor hash deseada sin agotar el peso de los datos de entrada. Sin embargo, después se encuentra la entrada, lo que le da el valor deseado, se puede comprobar fácilmente el hash. En consecuencia, un hash criptográfico es una buena manera de la «prueba de trabajo» Bitcoin.
En más detalle, con el fin de unidad smaynit debe primero recoger una nueva transacción bloque. Entonces es necesario para producir un bloque de hash para producir valor hash (esencialmente aleatoria manera) del bloque. Si el valor hash comienza con 16 ceros, el bloque se considera que ha confirmado y enviado a la red Bitcoin. La mayoría de las veces un hash no es exitosa, por lo que cambia ligeramente la unidad y vuelva a intentarlo una y otra vez, el gasto de más de mil millones de operaciones de computación. Aproximadamente cada 10 minutos, alguien puede confirmar con éxito la unidad y el proceso comienza de nuevo. Esto es una reminiscencia de la lotería, que implica mineros, intentando por el intento, siempre y cuando alguien no se convierta en un "ganador". La complejidad del proceso de hash es difícil presentación visual: es más fácil encontrar un grano de arena en el conjunto de la arena de la Tierra que encontrar el valor hash válido. Para encontrar estos valores hash mineros utilizan centros de datos equipados con hardware especial para la minería.
Muchas explicaciones para este artículo, deliberadamente simplificado. Si quieres aprender más sobre el sistema y la minería Bitcoin, aconsejo estudiar mis artículos Difícil Bitcoin experiencia minera y duras lecciones de Bitcoins mineras . < br />
El algoritmo de hash SHA-256 se utiliza Bitcoin
Ahora voy a hablar de la función de hash utilizado Bitcoin, que se basa en la función hash criptográfica estándar, llamado SHA-256. El sistema utiliza Bitcoin "doble SHA-256." Esto significa que la función SHA-256 se lleva a cabo dos veces. Algoritmo SHA-256 es tan simple que puede realizar es, literalmente, sólo disponible lápiz y papel , y este algoritmo permite mezclar los datos de forma impredecible. El algoritmo toma como bloques de entrada de 64 bytes, criptográficamente procesa los datos y salidas de los 256 bits (32 bytes) de datos cifrados. El algoritmo utiliza una sola ronda, que se repite 64 veces. La siguiente ilustración muestra una ronda de un algoritmo que toma ocho bloques de 4 bytes, y por medio de H, realiza varias operaciones y proporciona nuevos valores de la A a la H.
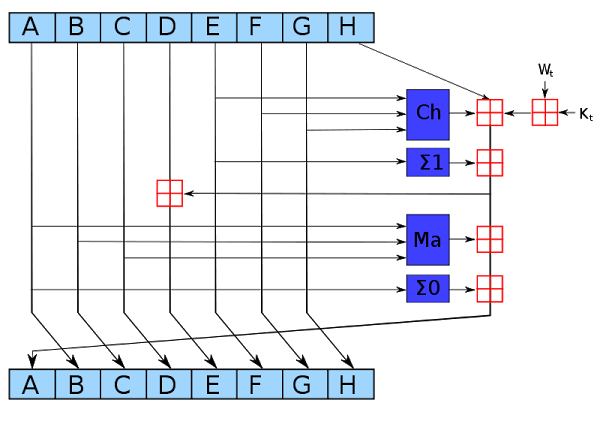
Ronda SHA-256, como una ilustración ejemplo de la Wikipedia, Autor kockmeyer, CC BY-SA 3.0 i>
Bloques azules oscuros agitaron bits de forma no lineal que es un reto para el criptoanálisis. (Si usted puede encontrar una manera más rápida de producir matemáticamente hashes exitosas, puede controlar los Bitcoins mineras). Celular Ch «selección" selecciona los bits de F o G, basado en los valores de las celdas de entrada E. Σ «suma» pedacitos rotados A (o E) generar tres cíclica cambió de versión, y luego agrega juntos modulo 2.
Celular Ma «mayoría» compruebe bits en cada posición A, B y C, y selecciona a 0 o 1, dependiendo de lo que el valor está en la mayoría. Los glóbulos rojos llevan una adición de 32 bits en la generación de nuevo valor para A y E. Entrar en peso basado en los datos de entrada ligeramente procesados. (Aquí es donde se introduce el bloque de entrada en el algoritmo.) Iniciar Kt es una constante determinada para cada ronda.
De acuerdo con la ilustración de arriba, un cambio ronda sólo A y E. El resto de valores se pasan sin cambios. El antiguo valor de A se convierte en el nuevo valor B, el antiguo valor de B se convierte en el nuevo valor de C, y así sucesivamente. Si bien cada ronda de SHA-256 cambia ligeramente los datos después de 64 rondas de los datos de entrada es completamente mezclado, dando valor hash de salida impredecible.
IBM 1401
Decidí correr el algoritmo en una computadora central IBM 1401. Apareció en 1959 y para mediados de los años 60 se convirtió en el equipo más vendido - mientras activamente explotado por más de 10 mil vehículos. Las computadoras en 1401 no era muy potente ordenador, incluso para 1960. Sin embargo, era asequible para las empresas medianas que antes no podían permitirse el lujo de tener un ordenador, ya que se puede alquilar por una pequeña cantidad de dinero -. $ 2500 por mes
El IBM 1401 no se utiliza chip de silicio. Además, en este equipo no había patatas fritas. Sus transistores fueron construidos en cristales semiconductores de germanio, que se utilizaron para el silicio. Transistores, junto con los otros componentes fueron instalados a bordo del tamaño de una tarjeta de juego, llamado Tarjeta SMS . El ordenador se utilizaron miles de tarjetas que se han instalado en un rack llamada "puerta". En IBM en 1401 y veinte de estas "puertas", que fueron presentadas para el mantenimiento de su equipo. En la ilustración visto una puerta abierta que proporciona acceso a los chips y cables.

La ilustración muestra un bastidor abierto (la llamada "puerta") de mainframe IBM 1401. La tarjeta SMS foto visto, conectado al circuito. Esta postura se ejecuta cinta i>
El principio de funcionamiento de un ordenador de este tipo es significativamente diferente de los PCs modernos. En este equipo no se utiliza bytes de 8 bits y el código de 6 bits sobre la base de decimal codificado en binario (BCD). Dado que esta máquina era una máquina calculadora para resolver los problemas económicos, se utiliza el decimal en lugar de aritmética binaria, y todos los personajes en la memoria tiene un valor numérico de 0 a 9. El equipo de memoria de núcleo magnético albergaba 4.000 caracteres. El módulo de expansión de memoria del tamaño de un lavavajillas, una mayor capacidad de memoria de 12.000 caracteres. Introducir datos en una computadora implementado con la ayuda de tarjetas perforadas. Los datos y los programas de lectura a partir de la tarjeta en el lector de tarjetas. Los datos de salida se imprime velocidad de la impresora de aguas residuales o su camino en los mapas.
Computer History Museo Computer History Museum en Mountain View tiene dos mainframe de IBM operable 1401. En uno de ellos me corrió el hash SHA -256. Para obtener más información acerca de IBM en 1401 le digo en su artículo sobre Fractales IBM 1401
.
Implementación de SHA-256 para IBM 1401
Seguramente mainframe de IBM en 1401 es la peor de todas las máquinas que podríamos elegir para ejecutar el algoritmo de hash SHA-256. Para el funcionamiento eficaz de este algoritmo es máquinas necesarias que pueden realizar operaciones bit a bit en palabras de 32 bits. Desafortunadamente, IBM 1401 no admite ninguna palabra de 32 bits o bytes. Este equipo trabaja con caracteres de 6 bits y no permite operaciones de bits. Además, en lugar binario, la aritmética decimal utilizado. Por lo tanto, el algoritmo en un ordenador en 1401 será lenta e inconveniente para el usuario.
Terminé usando un carácter un poco. Valor de 32 bits se almacena como 32 caracteres, o un "0" o "1". Se suponía que mi código para realizar operaciones de carácter bits, suma y multiplicación, comprobando cada personaje, y decidir qué hacer con él. Como era de esperarse, el rendimiento del código tomó mucho tiempo.
Después están escritos por mí asamblea código. El principio de todo el código se describe en los comentarios. Al final del código hay una tabla de constantes requeridas algoritmo SHA-256 en hexadecimal. Desde 1401 la computadora no admite el formato hexadecimal, que tenía que escribir sus propias rutinas para convertir formatos hexadecimales y binarios. En este artículo no voy a dar una explicación del código ensamblador IBM 1401 sólo se enfatiza que es muy diferente de la que los ordenadores modernos utilizados. Este código no causa la subrutina, y no produce resultados. Debido a la falta de registros de propósito general se lleva a cabo en la memoria.
Mirada Código bajo el alerón:
Texto Oculto
¿Puedo utilizar el mainframe de IBM viene de los años 60 del siglo pasado Mein Bitcoins? Decidí probar esto, a primera vista, una idea loca. He implementado un algoritmo de hash Bitcoin en código ensamblador para el IBM 1401 y probado en la práctica mediante la ejecución de un modelo viable de esta antigua mainframe.

Tarjeta, que se calcula utilizando el SHA-256 hashes en el mainframe IBM marcó tarjeta 1401.Za impresión visible en la impresora, que muestra la entrada del algoritmo y el hash resultante i>
Al final resultó que, con la ayuda de la computadora puede ser principal, pero el proceso lleva tanto tiempo que ni siquiera el tiempo de vida del universo puede no ser suficiente para un bloque único éxito de la minería.
Mientras que el hardware moderno permite calcular hashes miles de millones por segundo, el equipo en 1401 pasa 80 segundos para calcular un solo hash. Rendimiento Progreso de las computadoras en la última década hay que describe claramente la Ley de Moore.
Sacador tarjetas, participaron en el experimento, así como la impresión SHA-256 impresora de línea se muestra en las fotos (la primera tarjeta es una belleza - que no era fácil de romper este patrón). Tenga en cuenta que la segunda línea termina con un grupo de ceros; Esto significa un hash éxito.
El principio del sistema de la minería Bitcoin
En los últimos años, la moneda electrónica Bitcoin (Bitcoin), que los usuarios de Internet pueden enviar uno al otro, es muy popular. Para comprender la esencia criptomoneda actual, el sistema de Bitcoin se puede representar en forma de un libro de registro en el que un registro de los propietarios de las monedas digitales (Bitcoin) y el número de monedas que él / ella tiene. Los compradores Bitcoin puede transmitir la moneda digital de uno al otro.
Cabe señalar que el sistema de Bitcoin descentralizada: no tiene un único servidor de regulación, lo que seguir el curso de la operación. En cambio, estamos distribuyendo los registros de una red distribuida de miles de ordenadores en Internet.
La dificultad radica en el hecho de que tal sistema de distribución debe asegurar de alguna manera que el consentimiento de todos los usuarios en los registros. Es decir los usuarios de buena fe deben confirmar la validez de una transacción, aprobarlo, a pesar de la posible presencia de estafadores y trabajando lentamente su red. La solución a este problema fue la llamada "minería". Aproximadamente cada 10 minutos durante la unidad de salida de la minería confirmaron la transacción, como resultado, se le considera ser confirmada oficialmente.
El proceso de la minería, basado en una criptografía robusta, es extremadamente difícil, por lo que nadie puede controlar exactamente qué transacciones son la minería. En particular, la idea clave de Bitcoin es que el resultado de complejas y difíciles de obtener, pero es fácil de comprobar. Esta es la llamada tecnología «prueba de trabajo» («prueba de trabajo»).
El proceso de bloque de la minería requiere una enorme cantidad de costos de computación. Sin embargo, después de que la unidad ha sido certificado, los usuarios se asoman red puede fácilmente verificar su validez. La complejidad de la minería evita el uso fraudulento de Bitcoin, y la facilidad de unidad de verificación permite a los usuarios tener la confianza en la validez de la transacción.
Un efecto secundario de la minería es la adición de nuevo sistema de Bitcoin. En la actualidad, cualquier persona que confirmó la unidad recibe un 25 generada Bitcoin (ahora el coste del número de monedas virtuales en términos monetarios tradicionales se trata de 6000. USD). Esta promoción alienta "mineros" que trabajar duro y gastar sus recursos en la minería. Dada la oportunidad disponible para llegar a 6 dólares XX. Estados Unidos cada 10 minutos, la minería representa una verdadera "mina de oro", animando a los usuarios a gastar sumas considerables en hardware para la minería.

impresora de líneas y de mainframe de IBM en 1401, se presenta en la exposición del Museo de Historia de la Computación (Computer History Museum). Este equipo está funcionando mi programa. La consola se encuentra en la parte superior izquierda. Panel rectangular Negro en el equipo es una bastidores "puerta" que se reclinan, permitiendo el acceso para el mantenimiento. I>
El proceso de extracción extremadamente difícil, pero el resultado es muy fácil de comprobar. El Bitcoin Minería utiliza función hash de criptografía, llamado SHA-256 doble. Porción Hash toma los datos de entrada y lo reduce a un valor hash más pequeña (en este caso 256 bits).
Un algoritmo de hash criptográfica no cederá el valor hash deseada sin agotar el peso de los datos de entrada. Sin embargo, después se encuentra la entrada, lo que le da el valor deseado, se puede comprobar fácilmente el hash. En consecuencia, un hash criptográfico es una buena manera de la «prueba de trabajo» Bitcoin.
En más detalle, con el fin de unidad smaynit debe primero recoger una nueva transacción bloque. Entonces es necesario para producir un bloque de hash para producir valor hash (esencialmente aleatoria manera) del bloque. Si el valor hash comienza con 16 ceros, el bloque se considera que ha confirmado y enviado a la red Bitcoin. La mayoría de las veces un hash no es exitosa, por lo que cambia ligeramente la unidad y vuelva a intentarlo una y otra vez, el gasto de más de mil millones de operaciones de computación. Aproximadamente cada 10 minutos, alguien puede confirmar con éxito la unidad y el proceso comienza de nuevo. Esto es una reminiscencia de la lotería, que implica mineros, intentando por el intento, siempre y cuando alguien no se convierta en un "ganador". La complejidad del proceso de hash es difícil presentación visual: es más fácil encontrar un grano de arena en el conjunto de la arena de la Tierra que encontrar el valor hash válido. Para encontrar estos valores hash mineros utilizan centros de datos equipados con hardware especial para la minería.
Muchas explicaciones para este artículo, deliberadamente simplificado. Si quieres aprender más sobre el sistema y la minería Bitcoin, aconsejo estudiar mis artículos Difícil Bitcoin experiencia minera y duras lecciones de Bitcoins mineras . < br />
El algoritmo de hash SHA-256 se utiliza Bitcoin
Ahora voy a hablar de la función de hash utilizado Bitcoin, que se basa en la función hash criptográfica estándar, llamado SHA-256. El sistema utiliza Bitcoin "doble SHA-256." Esto significa que la función SHA-256 se lleva a cabo dos veces. Algoritmo SHA-256 es tan simple que puede realizar es, literalmente, sólo disponible lápiz y papel , y este algoritmo permite mezclar los datos de forma impredecible. El algoritmo toma como bloques de entrada de 64 bytes, criptográficamente procesa los datos y salidas de los 256 bits (32 bytes) de datos cifrados. El algoritmo utiliza una sola ronda, que se repite 64 veces. La siguiente ilustración muestra una ronda de un algoritmo que toma ocho bloques de 4 bytes, y por medio de H, realiza varias operaciones y proporciona nuevos valores de la A a la H.

Ronda SHA-256, como una ilustración ejemplo de la Wikipedia, Autor kockmeyer, CC BY-SA 3.0 i>
Bloques azules oscuros agitaron bits de forma no lineal que es un reto para el criptoanálisis. (Si usted puede encontrar una manera más rápida de producir matemáticamente hashes exitosas, puede controlar los Bitcoins mineras). Celular Ch «selección" selecciona los bits de F o G, basado en los valores de las celdas de entrada E. Σ «suma» pedacitos rotados A (o E) generar tres cíclica cambió de versión, y luego agrega juntos modulo 2.
Celular Ma «mayoría» compruebe bits en cada posición A, B y C, y selecciona a 0 o 1, dependiendo de lo que el valor está en la mayoría. Los glóbulos rojos llevan una adición de 32 bits en la generación de nuevo valor para A y E. Entrar en peso basado en los datos de entrada ligeramente procesados. (Aquí es donde se introduce el bloque de entrada en el algoritmo.) Iniciar Kt es una constante determinada para cada ronda.
De acuerdo con la ilustración de arriba, un cambio ronda sólo A y E. El resto de valores se pasan sin cambios. El antiguo valor de A se convierte en el nuevo valor B, el antiguo valor de B se convierte en el nuevo valor de C, y así sucesivamente. Si bien cada ronda de SHA-256 cambia ligeramente los datos después de 64 rondas de los datos de entrada es completamente mezclado, dando valor hash de salida impredecible.
IBM 1401
Decidí correr el algoritmo en una computadora central IBM 1401. Apareció en 1959 y para mediados de los años 60 se convirtió en el equipo más vendido - mientras activamente explotado por más de 10 mil vehículos. Las computadoras en 1401 no era muy potente ordenador, incluso para 1960. Sin embargo, era asequible para las empresas medianas que antes no podían permitirse el lujo de tener un ordenador, ya que se puede alquilar por una pequeña cantidad de dinero -. $ 2500 por mes
El IBM 1401 no se utiliza chip de silicio. Además, en este equipo no había patatas fritas. Sus transistores fueron construidos en cristales semiconductores de germanio, que se utilizaron para el silicio. Transistores, junto con los otros componentes fueron instalados a bordo del tamaño de una tarjeta de juego, llamado Tarjeta SMS . El ordenador se utilizaron miles de tarjetas que se han instalado en un rack llamada "puerta". En IBM en 1401 y veinte de estas "puertas", que fueron presentadas para el mantenimiento de su equipo. En la ilustración visto una puerta abierta que proporciona acceso a los chips y cables.

La ilustración muestra un bastidor abierto (la llamada "puerta") de mainframe IBM 1401. La tarjeta SMS foto visto, conectado al circuito. Esta postura se ejecuta cinta i>
El principio de funcionamiento de un ordenador de este tipo es significativamente diferente de los PCs modernos. En este equipo no se utiliza bytes de 8 bits y el código de 6 bits sobre la base de decimal codificado en binario (BCD). Dado que esta máquina era una máquina calculadora para resolver los problemas económicos, se utiliza el decimal en lugar de aritmética binaria, y todos los personajes en la memoria tiene un valor numérico de 0 a 9. El equipo de memoria de núcleo magnético albergaba 4.000 caracteres. El módulo de expansión de memoria del tamaño de un lavavajillas, una mayor capacidad de memoria de 12.000 caracteres. Introducir datos en una computadora implementado con la ayuda de tarjetas perforadas. Los datos y los programas de lectura a partir de la tarjeta en el lector de tarjetas. Los datos de salida se imprime velocidad de la impresora de aguas residuales o su camino en los mapas.
Computer History Museo Computer History Museum en Mountain View tiene dos mainframe de IBM operable 1401. En uno de ellos me corrió el hash SHA -256. Para obtener más información acerca de IBM en 1401 le digo en su artículo sobre Fractales IBM 1401
.
Implementación de SHA-256 para IBM 1401
Seguramente mainframe de IBM en 1401 es la peor de todas las máquinas que podríamos elegir para ejecutar el algoritmo de hash SHA-256. Para el funcionamiento eficaz de este algoritmo es máquinas necesarias que pueden realizar operaciones bit a bit en palabras de 32 bits. Desafortunadamente, IBM 1401 no admite ninguna palabra de 32 bits o bytes. Este equipo trabaja con caracteres de 6 bits y no permite operaciones de bits. Además, en lugar binario, la aritmética decimal utilizado. Por lo tanto, el algoritmo en un ordenador en 1401 será lenta e inconveniente para el usuario.
Terminé usando un carácter un poco. Valor de 32 bits se almacena como 32 caracteres, o un "0" o "1". Se suponía que mi código para realizar operaciones de carácter bits, suma y multiplicación, comprobando cada personaje, y decidir qué hacer con él. Como era de esperarse, el rendimiento del código tomó mucho tiempo.
Después están escritos por mí asamblea código. El principio de todo el código se describe en los comentarios. Al final del código hay una tabla de constantes requeridas algoritmo SHA-256 en hexadecimal. Desde 1401 la computadora no admite el formato hexadecimal, que tenía que escribir sus propias rutinas para convertir formatos hexadecimales y binarios. En este artículo no voy a dar una explicación del código ensamblador IBM 1401 sólo se enfatiza que es muy diferente de la que los ordenadores modernos utilizados. Este código no causa la subrutina, y no produce resultados. Debido a la falta de registros de propósito general se lleva a cabo en la memoria.
Mirada Código bajo el alerón:
Texto Oculto
& lt; code class = & quot; dos & quot; & gt; trabajo bitcoin * hash SHA-256 * Ken Shirriff http://righto.com ctl 6641 org 087 X1 dcw @ 000 @ org 092 X2 dcw @ 000 @ org 097 X3 dcw @ 000 @ org 333 inicia cs 299 r sw 001 lca 064, input0 mcw 064, 264 w * Inicializar marcas denominativas en mcw almacenamiento + s0, x3 wmloop sw 0 & amp; ma x3 @ 032 @ , x3 c + h7 + 32, x3 bu wmloop mcw + input-127, x3 * Ponga la entrada en warr [0] para Warr [15] mcw + warr, x1 mcw @ 128 @, tobinc b tobin * cronograma mensaje Compute serie w [0..63] mcw @ 16 @, i * i es el índice palabra 16-63 * x1 es inicio de warr [i-16], es decir, bit 0 (bit 0 de la izquierda, bit 31 a la derecha) mcw + warr, x1 wloop c @ 64 @, yo estaré wloopd * Calcular s0 mcw + s0, za x2 0, 31 & amp; x2 * Cero s0 * Añadir w [i -15] rightrotate 7 sw 7 & amp; x2 * Wordmark en el bit 7 (desde la izquierda) de s0 un 56 & amp; x1, 31 & amp; x2 * Derecho cambió: 32 + 31-7 = 24 bits de w [i-15], 31 = final de s0 un 63 & amp; x1, 6 & amp; x2 * Envuelto: 32 + 31 = final de w [i-15], 7-1 = bit 6 de s0 cw 7 & amp; x2 * Claro wordmark * Añadir w [i-15] rightrotate 18 sw 18 & amp; x2 * Wordmark en el bit 18 (desde la izquierda) de s0 un 45 & amp; x1, 31 & amp; x2 * Derecho cambió: 32 + 31-18 = bit 13 de w [i-15], 31 = final de s0 un 63 & amp; x1, 17 & amp; x2 * Envuelto: 32 + 31 = final de w [i-15], 18-1 = Bit 17 de s0 cw 18 & amp; x2 * Claro wordmark * Añadir w [i-15] SHIFTDERECHA 3 sw 3 & amp; x2 * Wordmark en el bit 3 (desde la izquierda) de s0 un 60 & amp; x1, 31 & amp; x2 * Derecho cambió: 32 + 31-3 = bit 28 de w [i-15], 31 = final de s0 cw amplificador 3 y; x2 * Claro wordmark * Convertir suma a xor mcw x1, x1tmp mcw + s0 + 31, x1 x1 * = extremo derecho de mcw s0 @ 032 @, x2 * Proceso de 32 bits b xor sw s0 * Restaurar wordmark despejado por xor mcw x1tmp, x1 * s1 Compute mcw + s1, x2 za 0, 31 & amp; x2 * Cero s1 * Añadir w [i-2] rightrotate 17 sw 17 & amp; x2 * Wordmark en el bit 17 (desde la izquierda) de s1 un 462 & amp; x1, 31 & amp ; x2 * Derecho cambió: 14 * 32 + 31-17 = bit 14 de w [i-2], 31 = final de s1 un 479 & amp; x1, 16 & amp; x2 * Envuelto: 14 * 32 + 31 = final de w [ i-2], 17-1 = mordí 16 de s1 cw 17 & amp; x2 * Claro wordmark * Añadir w [i-2] rightrotate 19 sw 19 & amp; x2 * Wordmark en el bit 19 (desde la izquierda) de s1 un 460 & amp; x1, 31 & amp; x2 * Derecho cambió: 14 * 32 + 31-19 = bit 12 de w [i-2], 31 = final de s1 un 479 & amp; x1, 18 & amp; x2 * Envuelto: 14 * 32 + 31 = final de w [i-2], 19-1 = mordí 18 de s1 cw 19 & amp; x2 * Claro wordmark * Añadir w [i-2] SHIFTDERECHA 10 sw 10 & amp; x2 * Wordmark en el bit 10 (desde la izquierda) de s1 un 469 & amp; x1 31 & amp; x2 * Derecho cambió: 14 * 32 + 31-10 = Bit 21 de w [i-2], 31 = final de s1 cw 10 & amp; x2 * Claro wordmark * Convertir suma a mcw xor + s1 + 31, x1 * x1 = extremo derecho de mcw s1 @ 032 @, x2 * Proceso de 32 bits b xor sw s1 * Restaurar wordmark despejado por xor * Calcular w [i]: = w [i-16] + s0 + w [i-7] + s1 x1tmp mcw, x1 un s1 + 31, s0 + 31 * Añadir s1 a S0 un 31 & amp; x1, s0 + 31 * Añadir w [i-16] para S0 un 319 & amp; x1, s0 + 31 * Agregar 9 * 32 31 = w [i-7] para S0 * Convertir suma poco a una suma mcw 32 bits + s0 + 31, x1 x1 * = extremo derecho de mcw s0 @ 032 @, x2 * Proceso de 32 bits b suma sw s0 * Restaurar Wordmark despejado por x1tmp suma mcw, mcw x1 s0 + 31, 543 & amp; x1 * Movimiento s0 a w [i] ma @ 032 @, x1 un 1, i MZ @ 0 @, ib wloop x1tmp dcw # 5 * Inicializar: Copia hexagonal h0init-h7init en binario wloopd MCW-h0 h7 + h0init-7, mcw x3 + h0, mcw x1 @ 064 @, tobinc * 8 * 8 dígitos hexadecimal b tobin * Inicializa ah desde MCW-h0 h7 @ 000 @, ILP x1 h0 MCW + 31 & amp; x1, a + 31 & amp; ma x1 @ 032 @, x1 c x1, @ 256 @ bu ILP mcw @ 000 @, bitidx * bitidx = i * 32 = poco mcw índice @ 000 @, kidx * kidx = i * 8 = índice de clave * Calcular s1 de correo mainlp mcw + e, x1 mcw + s1, x2 za 0, 31 & amp; x2 * Cero s1 * Añadir e rightrotate 6 sw 6 & amp; x2 * Wordmark en el bit 6 (desde la izquierda) de s1 un 25 & amp; x1, 31 & amp; x2 * Derecho cambió: 31-6 = Bit 25 de la e, 31 = final de s1 un 31 & amp; x1, 5 & amp; x2 * Envuelto: 31 = final del correo, 6-1 = bits 5 de s1 cw 6 & amp; x2 * Claro wordmark * Agregar e rightrotate 11 sw 11 & amp; x2 * Wordmark en el bit 11 (desde la izquierda) de s1 un 20 & amp; x1, 31 & amp; Derecho x2 * cambió: 31-11 = Bit 20 de la e 31 = final de s1 un 31 & amp; x1, 10 & amp; x2 * Envuelto: 31 = fin de la e, 11-1 = bit 10 de s1 cw 11 & amp; x2 * Claro wordmark * Añadir e rightrotate 25 sw 25 & amp; x2 * Wordmark en bit 25 (desde la izquierda) de s1 un 6 & amp; x1, 31 & amp; x2 * Derecho cambió: 31-25 = bit 6 de e, 31 = final de s1 un 31 & amp; x1, 24 & amp; x2 * Envuelto: 31 = fin de la e , 25-1 = 24 bits de s1 cw 25 & amp; x2 * Claro wordmark * Convertir suma a xor mcw + s1 + 31, x1 x1 * = extremo derecho de mcw s1 @ 032 @, x2 * Proceso de 32 bits b xor sw s1 * Restaurar wordmark despejado por xor * Calcular ch: elegir función mcw @ 000 @, x1 * x1 es el índice de 0 a 31 chl c e & amp; x1, @ 0 @ sea chzero mn f & amp; x1, ch & amp; x1 * para 1, seleccione f bit b chincr chzero mn g & amp; x1, ch & amp; x1 * durante 0, seleccione g poco chincr un 1, x1 mz @ 0 @, x1 c @ 032 @, x1 bu chl * Calcular temp1: k [i] + H + S1 + ch + w [i] cs 299 mcw + k-7, x3 * Convertir k [i] a binario en kidx ma temp1, x3 mcw + temp1, mcw x1 @ 008 @, tobinc * 8 dígitos hexadecimales b tobin mcw @
Fuente: geektimes.ru/company/hashflare/blog/252092/





















