1178
0.3
2015-06-20
Майнинг биткоинов на 55-летнем ветеране IBM 1401
Вдохновившись публикацией хабрапользователя mark_ablov «Майним Bitcoin с помощью бумаги и ручки», мы решили, что читателям гиктайм будет интересно, какие еще безумные идеи удалось реализовать автору оригинального поста — Кену Ширриффу.
Можно ли с помощью мэйнфрейма IBM родом из 60-х годов прошлого века майнить биткоины? Я решил проверить эту, на первый взгляд, сумасшедшую идею. Я внедрил хэш-алгоритм Bitcoin в ассемблерный код для IBM 1401 и проверил на практике, запустив его на работоспособной модели этого древнего мэйнфрейма.

Перфокарта, с помощью которой рассчитывались хэши SHA-256 на мэйнфрейме IBM 1401.За перфокартой видна распечатка на принтере, показывающая ввод алгоритма и итоговый хэш
Как оказалось, с помощью этого компьютера можно майнить, но данный процесс займет так много времени, что даже всего срока жизни Вселенной может оказаться не достаточно для успешного майнинга одного блока.
В то время как современное аппаратное обеспечение позволяет вычислять миллиарды хэшей в секунду, ЭВМ 1401 тратит по 80 секунд на вычисление единственного хэша. Прогресс производительности компьютеров за последние десятилетия налицо, что явственно описано законом Гордона Мура.
Перфокарты, участвовавшие в эксперименте, а также распечатка SHA-256 строчным принтером показаны на приведенной фотографии (первая перфокарта служит лишь для красоты – нелегко было пробить этот узор). Обратите внимание, что вторая строка заканчивается группой нулей; это означает успешный хэш.
Принцип майнинга системы Bitcoin
В последнее время электронная валюта Bitcoin (биткоин), которую интернет-пользователи могут передавать друг другу, пользуется большой популярностью. Для понимания сути работы данной криптовалюты, систему Bitcoin можно представить в виде некоего журнала учета, в котором хранятся записи о владельце цифровых монет (биткоинов) и количестве монет, которыми он/она располагает. Участники системы Bitcoin могут передавать цифровые монеты друг другу.
Следует отметить, что система Bitcoin децентрализована: у нее нет единого регулирующего сервера, который следил бы за ходом транзакций. Вместо этого осуществляется рассылка записей по распределенной сети из тысяч компьютеров в сети Интернет.
Сложность заключается в том, что подобная распределенная система должна каким-то образом обеспечивать согласие всех пользователей по поводу записей. То есть добросовестные пользователи должны подтвердить валидность транзакции, одобрить ее, несмотря на возможное присутствие мошенников и медленно работающие сети. Решением данной проблемы стал так называемый «майнинг». Примерно каждые 10 минут в процессе майнинга подтверждается блок выходящих транзакций, в результате он считается официально подтвержденным.
Процесс майнинга, основанный на надежной криптографии, крайне сложен, благодаря чему никто не может контролировать какие именно транзакции проходят майнинг. В частности, ключевой идеей системы Bitcoin является то, что результат работы получить сложно и трудно, но зато легко проверить. Речь идет о так называемой технологии «proof-of-work» («доказательство работы»).
Процесс майнинга блока требует огромного количества вычислительных затрат. Однако, после того как блок был подтвержден, пользователи одноранговой сети могут с легкостью проверить его валидность. Сложность майнинга предотвращает мошенническое использование Bitcoin, а легкость проверки достоверности блока позволяет пользователям быть уверенным в валидности транзакций.
Побочным эффектом майнинга является добавление новых биткоинов в систему. В настоящее время каждый, кто подтвердил блок, получает за это 25 сгенерированных биткоинов (сейчас стоимость этого количества виртуальных монеток в традиционном денежном выражении составляет около 6 тыс. долларов США). Такое поощрение стимулирует «майнеров» работать усердно и тратить свои ресурсы на майнинг. Учитывая имеющуюся возможность получать по 6 тыс. долларов США каждые 10 минут, майнинг представляется настоящей «золотой жилой», побуждая пользователей тратить значительные суммы на аппаратное обеспечение для майнинга.

Строчный принтер и Мэйнфрейм IBM 1401, представленные в экспозиции Музея компьютерной истории (Computer History Museum). Этот компьютер выполнял мою программу. Консоль расположена сверху слева. Темные прямоугольные панели на ЭВМ это «дверки» стоек, которые откидываются, предоставляя доступ для техобслуживания.
Процесс майнинга крайне сложен, но результат проверить очень легко. В майнинге биткоинов используется криптография с хэш-функцией под названием двойной SHA-256. Хэш берет порцию данных на входе и уменьшает ее до меньшего хэш-значения (в данном случае 256 бит).
Криптографический алгоритм хеширования не позволит получить нужное хэш-значение, не перебрав массу данных на входе. Однако после того как будет найден вход, который дает нужное значение, каждый может с легкостью проверить хэш. Следовательно, криптографическое хэширование является хорошим способом осуществления «proof-of-work» биткоинов.
Говоря более подробно, для того чтобы смайнить блок, вначале нужно собрать в блок новые транзакции. Затем нужно произвести хэширование блока для получения (по существу случайным образом) хэш-значение блока. Если хэш-значение начинается 16-ю нулями, блок считается успешно подтвержденным и посылается в сеть Bitcoin. Большинство времени хэш является не успешным, поэтому Вы слегка меняете блок и пытаетесь снова и снова, проведя не один миллиард вычислительных операций. Примерно каждые 10 минут кому-то удается успешно подтвердить блок и процесс начинается заново. Это напоминает лотерею, в которой участвуют майнеры, предпринимая попытку за попыткой, до тех пор, пока кто-нибудь не станет «победителем». Сложность процесса хеширования с трудом поддается визуальному представлению: легче найти песчинку во всем песке Земли, чем найти валидное хэш-значение. Для поиска таких хэш-значений майнеры используют дата-центры, оснащенные специальным аппаратным обеспечением для майнинга.
Многие пояснения в данной статье я намеренно упрощаю. Если Вы хотите подробнее ознакомиться с системой Bitcoin и майнингом, советую изучить мои статьи Нелегкий опыт добычи биткоинов и Суровые уроки майнинга биткоинов.
Хэш-алгоритм SHA-256, используемый Bitcoin
Теперь я рассмотрю функцию хэширования, используемую Bitcoin, которая основана на стандартной криптографической хэш-функции под названием SHA-256. В системе Bitcoin используется «двойной SHA-256». Это означает, что функция SHA-256 выполняется дважды. Алгоритм SHA-256 настолько прост, что выполнить его можно в буквальном смысле, имея в распоряжении лишь карандаш и бумагу, и при этом алгоритм позволяет смешивать данные непредсказуемым образом. Алгоритм принимает на входе блоки по 64 байта, обрабатывает данные криптографически и выдает 256 бит (32 байта) зашифрованных данных. В алгоритме используется один раунд, который повторяется 64 раза. На иллюстрации внизу показан один раунд алгоритма, который принимает по восемь 4-байтных блока, А через Н, выполняет несколько операций и выдает новые значения для А через Н.
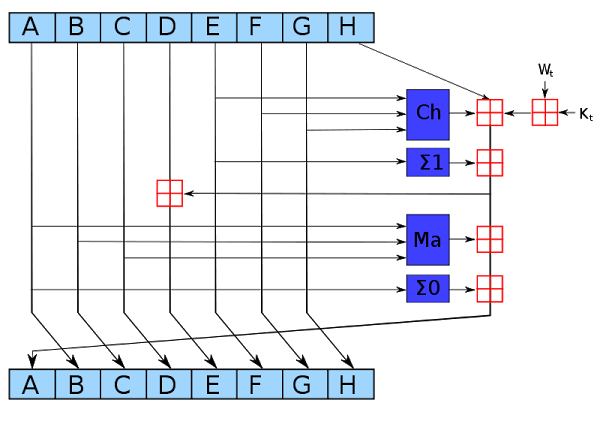
Раунд SHA-256, на примере иллюстрации из Wikipedia, автор kockmeyer, CC BY-SA 3.0
Темно-синие блоки перемешивают биты нелинейным образом, что представляет сложность для криптографического анализа. (Если Вам удастся найти математически более быстрый способ получения успешных хэшей, Вы сможете контролировать майнинг биткоинов). Ячейка Ch «выбор» выбирает биты от F или G, на основании значения входа E. Ячейки Σ «сумма» вращают биты A (или E) генерируя три циклических сдвинутых версии, и далее суммирует их вместе по модулю 2.
Ячейка Ma «большинство» проверяет биты в каждой позиции A, B, и C, и выбирает 0 или 1, в зависимости от того, какое значение находится в большинстве. Красные ячейки выполняют 32-битное добавление, генерируя новые значения для A и E. Вход Wt основан на слегка обработанных входных данных. (Именно здесь входной блок вводится в алгоритм.) Вход Kt это константа, определяемая для каждого раунда.
Согласно вышеприведенной иллюстрации, за раунд изменяются только A и E. Остальные значения пропускаются без изменений. Старое значение A становится новым значением B, старое значение B становится новым значением C, и так далее. Хотя каждый раунд SHA-256 изменяет данные незначительно, после 64 раундов входные данные полностью перемешиваются, давая на выходе непредсказуемое хэш-значение.
IBM 1401
Я решил выполнить данный алгоритм на мэйнфрейме IBM 1401. Этот компьютер появился в 1959 году и к середине 60-х годов стал самой продаваемой ЭВМ – в то время активно эксплуатировалось более 10 тысяч машин. ЭВМ 1401 была не слишком мощным компьютером даже для 1960 года. Однако она была по карману компаниям среднего бизнеса, которые ранее не могли позволить себе иметь компьютер, благодаря тому, что ее можно было взять в аренду за небольшие деньги – 2500 долларов США в месяц.
В IBM 1401 не использовались кремниевые микросхемы. Более того, в этой ЭВМ вообще не было микросхем. Ее транзисторы были построены на полупроводниках, кристаллах германия, которые использовались до кремния. Транзисторы, наряду с остальными компонентами, устанавливались на платы размером с игральные карты под названием SMS карты. В компьютере были задействованы тысячи таких карт, которые были установлены в виде стоек под названием «дверки». У IBM 1401 двадцать таких «дверок», которые выдвигались для техобслуживания компьютера. На приведенной иллюстрации видна одна открытая дверка, предоставляющая доступ к микросхемам и кабелям.

На иллюстрации показана открытая стойка (так называемая «дверка») Мэйнфрейм IBM 1401. На фотографии видны SMS карты, подключенные к цепи. Эта стойка управляет ленточными накопителями
Рабочий принцип такого компьютера значительно отличался от современных ПК. В этой ЭВМ использовались не 8-битные байты, а 6-битные символы на базе двоично-кодированного десятичного числа (BCD). Так как эта ЭВМ была счетной машиной для решения экономических задач, в ней использовалась десятичная, а не двоичная арифметика, и каждый символ в памяти имел цифровое значение от 0 до 9. Память компьютера на магнитных сердечниках вмещала 4000 символов. Модуль расширения памяти размером с посудомоечную машину, увеличивал емкость памяти на 12000 символов. Ввод данных в компьютер осуществлялся с помощью перфорированных карт. Данные и программы с карт считывал кардридер. Выходящие данные распечатывались скоростным сточным принтером или же пробивались на картах.
Музей компьютерной истории Computer History Museum в Маунтин-Вью располагает двумя работоспособными мэйнфреймами IBM 1401. На одном из них я запускал хэш-код SHA-256. Более подробно о IBM 1401 я рассказываю в своей статье Фракталы на IBM 1401
.
Выполнение SHA-256 на IBM 1401
Наверняка ЭВМ IBM 1401 является самой худшей из всех машин, которые можно было бы выбрать для выполнения хэш-алгоритма SHA-256. Для эффективной работы этому алгоритму необходимы машины, которые могут выполнять битовые операции в 32-битных словах. К сожалению, IBM 1401 не поддерживает ни 32-битные слова, ни байты. Эта ЭВМ работает с 6-битными символами и не позволяет выполнять битовые операции. Более того, в ней, вместо двоичной, использовалась десятичная арифметика. Следовательно, алгоритм на ЭВМ 1401 будет выполняться медленно и неудобным для пользователя образом.
Я закончил, используя один символ на бит. 32-битное значение сохранялось как 32 символ, либо «0» либо «1». Мой код должен был посимвольно выполнить битовые операции, умножения и сложения, проверяя каждый символ и решая, что с ним делать. Как и можно было ожидать, выполнение кода заняло много времени.
Далее я привожу написанный мной ассемблерный код. В целом принцип работы кода описан в комментариях. В конце кода есть таблица констант, необходимых алгоритму SHA-256 в шестнадцатеричном виде. Так как ЭВМ 1401 не поддерживает шестнадцатеричный формат, мне пришлось написать собственные подпрограммы для преобразования шестнадцатеричного и двоичного форматов. В этой статье я не буду приводить пояснения ассемблерного кода IBM 1401, подчеркну лишь, что он весьма отличается того, что используют современные компьютеры. Данный код не вызывает подпрограммы и не выдает результаты. В связи с отсутствием регистров общего назначения операции осуществляются в памяти.
Код ищите под спойлером:
Скрытый текст
Исполняемая программа была нанесена на 85 перфокарт (их вы уже видели в начале статьи). Я также сделал перфокарту с вводом хэш-алгоритма. Для того чтобы запустить программу, мне пришлось загрузить перфокарту в кардридер и нажать кнопку «Загрузка» («Load»). Кардридер обрабатывал по 800 карт в минуту. Таким образом, на загрузку программы ушло всего несколько секунд. Во время выполнения программы консоль компьютера (см. приведенную ниже иллюстрацию) лихорадочно мигала в течение 40 секунд. Наконец, принтер распечатал для меня итоговый хэш (распечатку вы также видели в начале статьи), и результаты были нанесены на новую перфокарту. Так как майнинг Bitcoin использует двойное хэширование SHA-256, процесс хэширования майнинга занял в два раза больше времени (80 секунд).

Усердная работа консоли IBM 1401 во время расчета хэша SHA-256
Сравнение производительности
ЭВМ IBM 1401 может вычислить двойной хэш SHA-256 за 80 секунд. На выполнение данной задачи компьютер потребляет около 3000 Вт мощности, примерно столько же сколько электроплита или сушилка для белья. В свое время базовая система IBM 1401 стоила 125600 долларов США. В реалиях 2015 года это составляет около миллиона долларов США. В то же время, сейчас вы можете купить USB флешку для майнинга за 50 долларов США, в которой имеется специализированная интегральная схема (ASIC USB майнер). Этот USB майнер выполняет 3,6 млрд. хэшей в секунду, потребляя при этом около 4 Вт.
Столь значительные показатели производительности обусловлены несколькими факторами: резким увеличением производительности компьютеров за последние 50 лет согласно закону Мура, потерей производительности, связанной с использованием десятичной арифметики в ЭВМ для решения коммерческих задач, которая была занята вычислением бинарного хэш-кода, а также выигрышем в быстродействии со стороны традиционного аппаратного обеспечения для майнинга биткоинов.
Подведем итоги. Для майнинга блока с учетом текущих требований к данному процессу, ЭВМ IBM 1401 понадобится около 5x10^14 лет (что в 40 000 раз превышает текущий возраст Вселенной). Стоимость израсходованной электроэнергии составит около 10^18 долларов США. В итоге Вы получите 25 биткоинов, чья стоимость в денежном выражении составит около 6000 долларов США. Итак, майнинг биткоинов на мэйнфрейме IBM 1401 прибыльным занятием не назовешь. На приведенных ниже фотографиях сравниваются компьютерные микросхемы 60-х годов прошлого века и современные варианты, наглядно демонстрируя технологический прогресс.


Слева: SMS карты, использовавшиеся в IBM 1401. Каждая карта состоит из множества компонентов с микросхемой. Количество таких карт в компьютере превышало тысячу. Справа: чип Bitfury ASIC позволяет майнить биткоины со скоростью 2-3 гигахэша в секунду. Источник фотографии: zeptobars (CC BY 3.0)
Передача данных по сети
Вы можете решить, что биткоины несовместимы с технологиями 60-х годов прошлого века из-за отсутствия возможности передачи данных по сети. Понадобится ли кому-то пересылать перфокарты с блочной цепью на другие компьютеры? Общение между компьютерами посредством сети появилось достаточно давно. Еще в 1941 году IBM поддерживала так называемый процесс телеметрической (дистанционной) обработки данных. В 60-е годы IBM 1401 можно было подключить к устройству передачи данных IBM 1009 (IBM 1009 Data Transmission Unit) — модему размером с посудомоечную машину, который позволял компьютерам обмениваться друг с другом данными по телефонной линии со скоростью до 300 символов в секунду. То есть, теоретически построение сети Bitcoin на базе технологий 60-х годов прошлого века вполне возможно. К сожалению, мне не удалось заполучить оборудование для телеобработки данных и проверить эту теорию.

Устройство передачи данных IBM 1009. Модем размером с посудомоечную машину появился в 1960 году. С его помощью можно было передавать до 300 символов в секунду по телефонной линии. Источник фотографии: Введение в системы обработки данных IBM Introduction to IBM Data Processing Systems).
Выводы
Использование SHA-256 в ассемблерном языке древнего мэйнфрейма стало непростым, но интересным опытом. Я ожидал более высокой производительности (даже по сравнению с моим множеством Мандельброта за 12 минут). Десятичная арифметика коммерческого компьютера это не лучший вариант для бинарного алгоритма наподобие SHA-256. Однако алгоритм майнинга биткоинов может быть выполнен даже на компьютере без интегральных микросхем. Поэтому, если вдруг некий временной коллапс перенесет меня в 1960 год, я смогу построить сеть Bitcoin.
Музей компьютерной истории в Маунтин-Вью по средам и субботам демонстрирует работающий IBM 1401. Если Вы случайно окажетесь неподалеку, Вам определенно стоит на это взглянуть, сверившись с расписанием работы. А если Вы расскажете сотрудникам музея, которые демонстрируют работающий IBM 1401 обо мне, возможно, они даже запустят мою программу Pi program.
Я хочу выразить благодарность Музею компьютерной истории (Computer History Museum) и членам команды по восстановлению ЭВМ 1401: Роберту Гарнеру, Эду Тэлену, Ван Снайдеру и, в особенности, Стэну Пэддоку. На веб-сайте этой команды ibm-1401.info много интересной информации об ЭВМ 1401 и работе по ее восстановлению.
Разъяснение
Стоит отметить, что я не смайнил реальный блок на IBM 1401 — Музею компьютерной истории это бы не понравилось. Как я уже говорил, имея рабочий IBM 1401, на майнинге заработать не удастся. Однако мне удалось внедрить и выполнить алгоритм SHA-256 на машине IBM 1401, доказав таким образом, что майнинг теоретически возможен. И открою секрет нахождения валидного хэша – я просто использовал уже смайненный блок.
Надеемся, наш перевод вам понравился

Источник: geektimes.ru/company/hashflare/blog/252092/
Можно ли с помощью мэйнфрейма IBM родом из 60-х годов прошлого века майнить биткоины? Я решил проверить эту, на первый взгляд, сумасшедшую идею. Я внедрил хэш-алгоритм Bitcoin в ассемблерный код для IBM 1401 и проверил на практике, запустив его на работоспособной модели этого древнего мэйнфрейма.

Перфокарта, с помощью которой рассчитывались хэши SHA-256 на мэйнфрейме IBM 1401.За перфокартой видна распечатка на принтере, показывающая ввод алгоритма и итоговый хэш
Как оказалось, с помощью этого компьютера можно майнить, но данный процесс займет так много времени, что даже всего срока жизни Вселенной может оказаться не достаточно для успешного майнинга одного блока.
В то время как современное аппаратное обеспечение позволяет вычислять миллиарды хэшей в секунду, ЭВМ 1401 тратит по 80 секунд на вычисление единственного хэша. Прогресс производительности компьютеров за последние десятилетия налицо, что явственно описано законом Гордона Мура.
Перфокарты, участвовавшие в эксперименте, а также распечатка SHA-256 строчным принтером показаны на приведенной фотографии (первая перфокарта служит лишь для красоты – нелегко было пробить этот узор). Обратите внимание, что вторая строка заканчивается группой нулей; это означает успешный хэш.
Принцип майнинга системы Bitcoin
В последнее время электронная валюта Bitcoin (биткоин), которую интернет-пользователи могут передавать друг другу, пользуется большой популярностью. Для понимания сути работы данной криптовалюты, систему Bitcoin можно представить в виде некоего журнала учета, в котором хранятся записи о владельце цифровых монет (биткоинов) и количестве монет, которыми он/она располагает. Участники системы Bitcoin могут передавать цифровые монеты друг другу.
Следует отметить, что система Bitcoin децентрализована: у нее нет единого регулирующего сервера, который следил бы за ходом транзакций. Вместо этого осуществляется рассылка записей по распределенной сети из тысяч компьютеров в сети Интернет.
Сложность заключается в том, что подобная распределенная система должна каким-то образом обеспечивать согласие всех пользователей по поводу записей. То есть добросовестные пользователи должны подтвердить валидность транзакции, одобрить ее, несмотря на возможное присутствие мошенников и медленно работающие сети. Решением данной проблемы стал так называемый «майнинг». Примерно каждые 10 минут в процессе майнинга подтверждается блок выходящих транзакций, в результате он считается официально подтвержденным.
Процесс майнинга, основанный на надежной криптографии, крайне сложен, благодаря чему никто не может контролировать какие именно транзакции проходят майнинг. В частности, ключевой идеей системы Bitcoin является то, что результат работы получить сложно и трудно, но зато легко проверить. Речь идет о так называемой технологии «proof-of-work» («доказательство работы»).
Процесс майнинга блока требует огромного количества вычислительных затрат. Однако, после того как блок был подтвержден, пользователи одноранговой сети могут с легкостью проверить его валидность. Сложность майнинга предотвращает мошенническое использование Bitcoin, а легкость проверки достоверности блока позволяет пользователям быть уверенным в валидности транзакций.
Побочным эффектом майнинга является добавление новых биткоинов в систему. В настоящее время каждый, кто подтвердил блок, получает за это 25 сгенерированных биткоинов (сейчас стоимость этого количества виртуальных монеток в традиционном денежном выражении составляет около 6 тыс. долларов США). Такое поощрение стимулирует «майнеров» работать усердно и тратить свои ресурсы на майнинг. Учитывая имеющуюся возможность получать по 6 тыс. долларов США каждые 10 минут, майнинг представляется настоящей «золотой жилой», побуждая пользователей тратить значительные суммы на аппаратное обеспечение для майнинга.

Строчный принтер и Мэйнфрейм IBM 1401, представленные в экспозиции Музея компьютерной истории (Computer History Museum). Этот компьютер выполнял мою программу. Консоль расположена сверху слева. Темные прямоугольные панели на ЭВМ это «дверки» стоек, которые откидываются, предоставляя доступ для техобслуживания.
Процесс майнинга крайне сложен, но результат проверить очень легко. В майнинге биткоинов используется криптография с хэш-функцией под названием двойной SHA-256. Хэш берет порцию данных на входе и уменьшает ее до меньшего хэш-значения (в данном случае 256 бит).
Криптографический алгоритм хеширования не позволит получить нужное хэш-значение, не перебрав массу данных на входе. Однако после того как будет найден вход, который дает нужное значение, каждый может с легкостью проверить хэш. Следовательно, криптографическое хэширование является хорошим способом осуществления «proof-of-work» биткоинов.
Говоря более подробно, для того чтобы смайнить блок, вначале нужно собрать в блок новые транзакции. Затем нужно произвести хэширование блока для получения (по существу случайным образом) хэш-значение блока. Если хэш-значение начинается 16-ю нулями, блок считается успешно подтвержденным и посылается в сеть Bitcoin. Большинство времени хэш является не успешным, поэтому Вы слегка меняете блок и пытаетесь снова и снова, проведя не один миллиард вычислительных операций. Примерно каждые 10 минут кому-то удается успешно подтвердить блок и процесс начинается заново. Это напоминает лотерею, в которой участвуют майнеры, предпринимая попытку за попыткой, до тех пор, пока кто-нибудь не станет «победителем». Сложность процесса хеширования с трудом поддается визуальному представлению: легче найти песчинку во всем песке Земли, чем найти валидное хэш-значение. Для поиска таких хэш-значений майнеры используют дата-центры, оснащенные специальным аппаратным обеспечением для майнинга.
Многие пояснения в данной статье я намеренно упрощаю. Если Вы хотите подробнее ознакомиться с системой Bitcoin и майнингом, советую изучить мои статьи Нелегкий опыт добычи биткоинов и Суровые уроки майнинга биткоинов.
Хэш-алгоритм SHA-256, используемый Bitcoin
Теперь я рассмотрю функцию хэширования, используемую Bitcoin, которая основана на стандартной криптографической хэш-функции под названием SHA-256. В системе Bitcoin используется «двойной SHA-256». Это означает, что функция SHA-256 выполняется дважды. Алгоритм SHA-256 настолько прост, что выполнить его можно в буквальном смысле, имея в распоряжении лишь карандаш и бумагу, и при этом алгоритм позволяет смешивать данные непредсказуемым образом. Алгоритм принимает на входе блоки по 64 байта, обрабатывает данные криптографически и выдает 256 бит (32 байта) зашифрованных данных. В алгоритме используется один раунд, который повторяется 64 раза. На иллюстрации внизу показан один раунд алгоритма, который принимает по восемь 4-байтных блока, А через Н, выполняет несколько операций и выдает новые значения для А через Н.

Раунд SHA-256, на примере иллюстрации из Wikipedia, автор kockmeyer, CC BY-SA 3.0
Темно-синие блоки перемешивают биты нелинейным образом, что представляет сложность для криптографического анализа. (Если Вам удастся найти математически более быстрый способ получения успешных хэшей, Вы сможете контролировать майнинг биткоинов). Ячейка Ch «выбор» выбирает биты от F или G, на основании значения входа E. Ячейки Σ «сумма» вращают биты A (или E) генерируя три циклических сдвинутых версии, и далее суммирует их вместе по модулю 2.
Ячейка Ma «большинство» проверяет биты в каждой позиции A, B, и C, и выбирает 0 или 1, в зависимости от того, какое значение находится в большинстве. Красные ячейки выполняют 32-битное добавление, генерируя новые значения для A и E. Вход Wt основан на слегка обработанных входных данных. (Именно здесь входной блок вводится в алгоритм.) Вход Kt это константа, определяемая для каждого раунда.
Согласно вышеприведенной иллюстрации, за раунд изменяются только A и E. Остальные значения пропускаются без изменений. Старое значение A становится новым значением B, старое значение B становится новым значением C, и так далее. Хотя каждый раунд SHA-256 изменяет данные незначительно, после 64 раундов входные данные полностью перемешиваются, давая на выходе непредсказуемое хэш-значение.
IBM 1401
Я решил выполнить данный алгоритм на мэйнфрейме IBM 1401. Этот компьютер появился в 1959 году и к середине 60-х годов стал самой продаваемой ЭВМ – в то время активно эксплуатировалось более 10 тысяч машин. ЭВМ 1401 была не слишком мощным компьютером даже для 1960 года. Однако она была по карману компаниям среднего бизнеса, которые ранее не могли позволить себе иметь компьютер, благодаря тому, что ее можно было взять в аренду за небольшие деньги – 2500 долларов США в месяц.
В IBM 1401 не использовались кремниевые микросхемы. Более того, в этой ЭВМ вообще не было микросхем. Ее транзисторы были построены на полупроводниках, кристаллах германия, которые использовались до кремния. Транзисторы, наряду с остальными компонентами, устанавливались на платы размером с игральные карты под названием SMS карты. В компьютере были задействованы тысячи таких карт, которые были установлены в виде стоек под названием «дверки». У IBM 1401 двадцать таких «дверок», которые выдвигались для техобслуживания компьютера. На приведенной иллюстрации видна одна открытая дверка, предоставляющая доступ к микросхемам и кабелям.

На иллюстрации показана открытая стойка (так называемая «дверка») Мэйнфрейм IBM 1401. На фотографии видны SMS карты, подключенные к цепи. Эта стойка управляет ленточными накопителями
Рабочий принцип такого компьютера значительно отличался от современных ПК. В этой ЭВМ использовались не 8-битные байты, а 6-битные символы на базе двоично-кодированного десятичного числа (BCD). Так как эта ЭВМ была счетной машиной для решения экономических задач, в ней использовалась десятичная, а не двоичная арифметика, и каждый символ в памяти имел цифровое значение от 0 до 9. Память компьютера на магнитных сердечниках вмещала 4000 символов. Модуль расширения памяти размером с посудомоечную машину, увеличивал емкость памяти на 12000 символов. Ввод данных в компьютер осуществлялся с помощью перфорированных карт. Данные и программы с карт считывал кардридер. Выходящие данные распечатывались скоростным сточным принтером или же пробивались на картах.
Музей компьютерной истории Computer History Museum в Маунтин-Вью располагает двумя работоспособными мэйнфреймами IBM 1401. На одном из них я запускал хэш-код SHA-256. Более подробно о IBM 1401 я рассказываю в своей статье Фракталы на IBM 1401
.
Выполнение SHA-256 на IBM 1401
Наверняка ЭВМ IBM 1401 является самой худшей из всех машин, которые можно было бы выбрать для выполнения хэш-алгоритма SHA-256. Для эффективной работы этому алгоритму необходимы машины, которые могут выполнять битовые операции в 32-битных словах. К сожалению, IBM 1401 не поддерживает ни 32-битные слова, ни байты. Эта ЭВМ работает с 6-битными символами и не позволяет выполнять битовые операции. Более того, в ней, вместо двоичной, использовалась десятичная арифметика. Следовательно, алгоритм на ЭВМ 1401 будет выполняться медленно и неудобным для пользователя образом.
Я закончил, используя один символ на бит. 32-битное значение сохранялось как 32 символ, либо «0» либо «1». Мой код должен был посимвольно выполнить битовые операции, умножения и сложения, проверяя каждый символ и решая, что с ним делать. Как и можно было ожидать, выполнение кода заняло много времени.
Далее я привожу написанный мной ассемблерный код. В целом принцип работы кода описан в комментариях. В конце кода есть таблица констант, необходимых алгоритму SHA-256 в шестнадцатеричном виде. Так как ЭВМ 1401 не поддерживает шестнадцатеричный формат, мне пришлось написать собственные подпрограммы для преобразования шестнадцатеричного и двоичного форматов. В этой статье я не буду приводить пояснения ассемблерного кода IBM 1401, подчеркну лишь, что он весьма отличается того, что используют современные компьютеры. Данный код не вызывает подпрограммы и не выдает результаты. В связи с отсутствием регистров общего назначения операции осуществляются в памяти.
Код ищите под спойлером:
Скрытый текст
<code class="dos">job bitcoin * SHA-256 hash * Ken Shirriff http://righto.com ctl 6641 org 087 X1 dcw @000@ org 092 X2 dcw @000@ org 097 X3 dcw @000@ org 333 start cs 299 r sw 001 lca 064, input0 mcw 064, 264 w * Initialize word marks on storage mcw +s0, x3 wmloop sw 0&x3 ma @032@, x3 c +h7+32, x3 bu wmloop mcw +input-127, x3 * Put input into warr[0] to warr[15] mcw +warr, x1 mcw @128@, tobinc b tobin * Compute message schedule array w[0..63] mcw @16@, i * i is word index 16-63 * x1 is start of warr[i-16], i.e. bit 0 (bit 0 on left, bit 31 on right) mcw +warr, x1 wloop c @64@, i be wloopd * Compute s0 mcw +s0, x2 za +0, 31&x2 * Zero s0 * Add w[i-15] rightrotate 7 sw 7&x2 * Wordmark at bit 7 (from left) of s0 a 56&x1, 31&x2 * Right shifted: 32+31-7 = bit 24 of w[i-15], 31 = end of s0 a 63&x1, 6&x2 * Wrapped: 32+31 = end of w[i-15], 7-1 = bit 6 of s0 cw 7&x2 * Clear wordmark * Add w[i-15] rightrotate 18 sw 18&x2 * Wordmark at bit 18 (from left) of s0 a 45&x1, 31&x2 * Right shifted: 32+31-18 = bit 13 of w[i-15], 31 = end of s0 a 63&x1, 17&x2 * Wrapped: 32+31 = end of w[i-15], 18-1 = bit 17 of s0 cw 18&x2 * Clear wordmark * Add w[i-15] rightshift 3 sw 3&x2 * Wordmark at bit 3 (from left) of s0 a 60&x1, 31&x2 * Right shifted: 32+31-3 = bit 28 of w[i-15], 31 = end of s0 cw 3&x2 * Clear wordmark * Convert sum to xor mcw x1, x1tmp mcw +s0+31, x1 * x1 = right end of s0 mcw @032@, x2 * Process 32 bits b xor sw s0 * Restore wordmark cleared by xor mcw x1tmp, x1 * Compute s1 mcw +s1, x2 za +0, 31&x2 * Zero s1 * Add w[i-2] rightrotate 17 sw 17&x2 * Wordmark at bit 17 (from left) of s1 a 462&x1, 31&x2 * Right shifted: 14*32+31-17 = bit 14 of w[i-2], 31 = end of s1 a 479&x1, 16&x2 * Wrapped: 14*32+31 = end of w[i-2], 17-1 = bit 16 of s1 cw 17&x2 * Clear wordmark * Add w[i-2] rightrotate 19 sw 19&x2 * Wordmark at bit 19 (from left) of s1 a 460&x1, 31&x2 * Right shifted: 14*32+31-19 = bit 12 of w[i-2], 31 = end of s1 a 479&x1, 18&x2 * Wrapped: 14*32+31 = end of w[i-2], 19-1 = bit 18 of s1 cw 19&x2 * Clear wordmark * Add w[i-2] rightshift 10 sw 10&x2 * Wordmark at bit 10 (from left) of s1 a 469&x1, 31&x2 * Right shifted: 14*32+31-10 = bit 21 of w[i-2], 31 = end of s1 cw 10&x2 * Clear wordmark * Convert sum to xor mcw +s1+31, x1 * x1 = right end of s1 mcw @032@, x2 * Process 32 bits b xor sw s1 * Restore wordmark cleared by xor * Compute w[i] := w[i-16] + s0 + w[i-7] + s1 mcw x1tmp, x1 a s1+31, s0+31 * Add s1 to s0 a 31&x1, s0+31 * Add w[i-16] to s0 a 319&x1, s0+31 * Add 9*32+31 = w[i-7] to s0 * Convert bit sum to 32-bit sum mcw +s0+31, x1 * x1 = right end of s0 mcw @032@, x2 * Process 32 bits b sum sw s0 * Restore wordmark cleared by sum mcw x1tmp, x1 mcw s0+31, 543&x1 * Move s0 to w[i] ma @032@, x1 a +1, i mz @0@, i b wloop x1tmp dcw #5 * Initialize: Copy hex h0init-h7init into binary h0-h7 wloopd mcw +h0init-7, x3 mcw +h0, x1 mcw @064@, tobinc * 8*8 hex digits b tobin * Initialize a-h from h0-h7 mcw @000@, x1 ilp mcw h0+31&x1, a+31&x1 ma @032@, x1 c x1, @256@ bu ilp mcw @000@, bitidx * bitidx = i*32 = bit index mcw @000@, kidx * kidx = i*8 = key index * Compute s1 from e mainlp mcw +e, x1 mcw +s1, x2 za +0, 31&x2 * Zero s1 * Add e rightrotate 6 sw 6&x2 * Wordmark at bit 6 (from left) of s1 a 25&x1, 31&x2 * Right shifted: 31-6 = bit 25 of e, 31 = end of s1 a 31&x1, 5&x2 * Wrapped: 31 = end of e, 6-1 = bit 5 of s1 cw 6&x2 * Clear wordmark * Add e rightrotate 11 sw 11&x2 * Wordmark at bit 11 (from left) of s1 a 20&x1, 31&x2 * Right shifted: 31-11 = bit 20 of e, 31 = end of s1 a 31&x1, 10&x2 * Wrapped: 31 = end of e, 11-1 = bit 10 of s1 cw 11&x2 * Clear wordmark * Add e rightrotate 25 sw 25&x2 * Wordmark at bit 25 (from left) of s1 a 6&x1, 31&x2 * Right shifted: 31-25 = bit 6 of e, 31 = end of s1 a 31&x1, 24&x2 * Wrapped: 31 = end of e, 25-1 = bit 24 of s1 cw 25&x2 * Clear wordmark * Convert sum to xor mcw +s1+31, x1 * x1 = right end of s1 mcw @032@, x2 * Process 32 bits b xor sw s1 * Restore wordmark cleared by xor * Compute ch: choose function mcw @000@, x1 * x1 is index from 0 to 31 chl c e&x1, @0@ be chzero mn f&x1, ch&x1 * for 1, select f bit b chincr chzero mn g&x1, ch&x1 * for 0, select g bit chincr a +1, x1 mz @0@, x1 c @032@, x1 bu chl * Compute temp1: k[i] + h + S1 + ch + w[i] cs 299 mcw +k-7, x3 * Convert k[i] to binary in temp1 ma kidx, x3 mcw +temp1, x1 mcw @008@, tobinc * 8 hex digits b tobin mcw @237@, x3 mcw +temp1, x1 mcw @008@, tobinc b tohex a h+31, temp1+31 * +h a s1+31, temp1+31 * +s1 a ch+31, temp1+31 * +ch mcw bitidx, x1 a warr+31&x1, temp1+31 * + w[i] * Convert bit sum to 32-bit sum mcw +temp1+31, x1 * x1 = right end of temp1 b sum * Compute s0 from a mcw +a, x1 mcw +s0, x2 za +0, 31&x2 * Zero s0 * Add a rightrotate 2 sw 2&x2 * Wordmark at bit 2 (from left) of s0 a 29&x1, 31&x2 * Right shifted: 31-2 = bit 29 of a, 31 = end of s0 a 31&x1, 1&x2 * Wrapped: 31 = end of a, 2-1 = bit 1 of s0 cw 2&x2 * Clear wordmark * Add a rightrotate 13 sw 13&x2 * Wordmark at bit 13 (from left) of s0 a 18&x1, 31&x2 * Right shifted: 31-13 = bit 18 of a, 31 = end of s0 a 31&x1, 12&x2 * Wrapped: 31 = end of a, 13-1 = bit 12 of s0 cw 13&x2 * Clear wordmark * Add a rightrotate 22 sw 22&x2 * Wordmark at bit 22 (from left) of s0 a 9&x1, 31&x2 * Right shifted: 31-22 = bit 9 of a, 31 = end of s0 a 31&x1, 21&x2 * Wrapped: 31 = end of a, 22-1 = bit 21 of s0 cw 22&x2 * Clear wordmark * Convert sum to xor mcw +s0+31, x1 * x1 = right end of s0 mcw @032@, x2 * Process 32 bits b xor sw s0 * Restore wordmark cleared by xor * Compute maj(a, b, c): majority function za +0, maj+31 a a+31, maj+31 a b+31, maj+31 a c+31, maj+31 mz @0@, maj+31 mcw @000@, x1 * x1 is index from 0 to 31 mjl c maj&x1, @2@ bh mjzero mn @1@, maj&x1 * majority of the 3 bits is 1 b mjincr mjzero mn @0@, maj&x1 * majority of the 3 bits is 0 mjincr a +1, x1 mz @0@, x1 c @032@, x1 bu mjl * Compute temp2: S0 + maj za +0, temp2+31 a s0+31, temp2+31 a maj+31, temp2+31 * Convert bit sum to 32-bit sum mcw +temp2+31, x1 * x1 = right end of temp1 b sum mcw g+31, h+31 * h := g mcw f+31, g+31 * g := f mcw e+31, f+31 * f := e za +0, e+31 * e := d + temp1 a d+31, e+31 a temp1+31, e+31 mcw +e+31, x1 * Convert sum to 32-bit sum b sum mcw c+31, d+31 * d := c mcw b+31, c+31 * c := b mcw a+31, b+31 * b := a za +0, a+31 * a := temp1 + temp2 a temp1+31, a+31 a temp2+31, a+31 mcw +a+31, x1 * Convert sum to 32-bit sum b sum a @8@, kidx * Increment kidx by 8 chars mz @0@, kidx ma @032@, bitidx * Increment bitidx by 32 bits c @!48@, bitidx * Compare to 2048 bu mainlp * Add a-h to h0-h7 cs 299 mcw @00000@, x1tmp add1 mcw x1tmp, x1 a a+31&x1, h0+31&x1 ma +h0+31, x1 * Convert sum to 32-bit sum b sum ma @032@, x1tmp c @00256@, x1tmp bu add1 mcw @201@, x3 mcw +h0, x1 mcw @064@, tobinc b tohex w mcw 280, 180 p p finis h b finis * Converts sum of bits to xor * X1 is right end of word * X2 is bit count * Note: clears word marks xor sbr xorx&3 xorl c @000@, x2 be xorx xorfix mz @0@, 0&x1 * Clear zone c 0&x1, @2@ bh xorok sw 0&x1 * Subtract 2 and loop s +2, 0&x1 cw 0&x1 b xorfix xorok ma @I9I@, x1 * x1 -= 1 s +1, x2 * x2 -= 1 mz @0@, x2 b xorl * loop xorx b @000@ * Converts sum of bits to sum (i.e. propagate carries if digit > 1) * X1 is right end of word * Ends at word mark sum sbr sumx&3 suml mz @0@, 0&x1 * Clear zone c 0&x1, @2@ * If digit is <2, then ok bh sumok s +2, 0&x1 * Subtract 2 from digit bwz suml, 0&x1, 1 * Skip carry if at wordmark a @1@, 15999&x1 * Add 1 to previous position b suml * Loop sumok bwz sumx,0&x1,1 * Quit if at wordmark ma @I9I@, x1 * x1 -= 1 b suml * loop sumx b @000@ * return * Converts binary to string of hex digits * X1 points to start (left) of binary * X3 points to start (left) of hex buffer * X1, X2, X3 destroyed * tobinc holds count (# of hex digits) tohex sbr tohexx&3 tohexl c @000@, tobinc * check counter be tohexx s @1@, tobinc * decrement counter mz @0@, tobinc b tohex4 mcw hexchr, 0&x3 ma @004@, X1 ma @001@, X3 b tohexl * loop tohexx b @000@ * X1 points to 4 bits * Convert to hex char and write into hexchr * X2 destroyed tohex4 sbr tohx4x&3 mcw @000@, x2 c 3&X1, @1@ bu tohx1 a +1, x2 tohx1 c 2&X1, @1@ bu tohx2 a +2, x2 tohx2 c 1&x1, @1@ bu tohx4 a +4, x2 tohx4 c 0&x1, @1@ bu tohx8 a +8, x2 tohx8 mz @0@, x2 mcw hextab-15&x2, hexchr tohx4x b @000@ * Converts string of hex digits to binary * X3 points to start (left) of hex digits * X1 points to start (left) of binary digits * tobinc holds count (# of hex digits) * X1, X3 destroyed tobin sbr tobinx&3 tobinl c @000@, tobinc * check counter be tobinx s @1@, tobinc * decrement counter mz @0@, tobinc mcw 0&X3, hexchr b tobin4 * convert 1 char ma @004@, X1 ma @001@, X3 b tobinl * loop tobinx b @000@ tobinc dcw @000@ * Convert hex digit to binary * Digit in hexchr (destroyed) * Bits written to x1, ..., x1+3 tobin4 sbr tobn4x&3 mcw @0000@, 3+x1 * Start with zero bits bwz norm,hexchr,2 * Branch if no zone mcw @1@, 0&X1 a @1@, hexchr * Convert letter to value: A (1) -> 2, F (6) -> 7 mz @0@, hexchr b tob4 norm c @8@, hexchr bl tob4 mcw @1@, 0&X1 s @8@, hexchr mz @0@, hexchr tob4 c @4@, hexchr bl tob2 mcw @1@, 1&X1 s @4@, hexchr mz @0@, hexchr tob2 c @2@, hexchr bl tob1 mcw @1@, 2&X1 s @2@, hexchr mz @0@, hexchr tob1 c @1@, hexchr bl tobn4x mcw @1@, 3&X1 tobn4x b @000@ * Message schedule array is 64 entries of 32 bits = 2048 bits. org 3000 warr equ 3000 s0 equ warr+2047 *32 bits s1 equ s0+32 ch equ s1+32 *32 bits temp1 equ ch+32 *32 bits temp2 equ temp1+32 *32 bits maj equ temp2+32 *32 bits a equ maj+32 b equ a+32 c equ b+32 d equ c+32 e equ d+32 f equ e+32 g equ f+32 h equ g+32 h0 equ h+32 h1 equ h0+32 h2 equ h1+32 h3 equ h2+32 h4 equ h3+32 h5 equ h4+32 h6 equ h5+32 h7 equ h6+32 org h7+32 hexchr dcw @0@ hextab dcw @0123456789abcdef@ i dcw @00@ * Loop counter for w computation bitidx dcw #3 kidx dcw #3 * 64 round constants for SHA-256 k dcw @428a2f98@ dcw @71374491@ dcw @b5c0fbcf@ dcw @e9b5dba5@ dcw @3956c25b@ dcw @59f111f1@ dcw @923f82a4@ dcw @ab1c5ed5@ dcw @d807aa98@ dcw @12835b01@ dcw @243185be@ dcw @550c7dc3@ dcw @72be5d74@ dcw @80deb1fe@ dcw @9bdc06a7@ dcw @c19bf174@ dcw @e49b69c1@ dcw @efbe4786@ dcw @0fc19dc6@ dcw @240ca1cc@ dcw @2de92c6f@ dcw @4a7484aa@ dcw @5cb0a9dc@ dcw @76f988da@ dcw @983e5152@ dcw @a831c66d@ dcw @b00327c8@ dcw @bf597fc7@ dcw @c6e00bf3@ dcw @d5a79147@ dcw @06ca6351@ dcw @14292967@ dcw @27b70a85@ dcw @2e1b2138@ dcw @4d2c6dfc@ dcw @53380d13@ dcw @650a7354@ dcw @766a0abb@ dcw @81c2c92e@ dcw @92722c85@ dcw @a2bfe8a1@ dcw @a81a664b@ dcw @c24b8b70@ dcw @c76c51a3@ dcw @d192e819@ dcw @d6990624@ dcw @f40e3585@ dcw @106aa070@ dcw @19a4c116@ dcw @1e376c08@ dcw @2748774c@ dcw @34b0bcb5@ dcw @391c0cb3@ dcw @4ed8aa4a@ dcw @5b9cca4f@ dcw @682e6ff3@ dcw @748f82ee@ dcw @78a5636f@ dcw @84c87814@ dcw @8cc70208@ dcw @90befffa@ dcw @a4506ceb@ dcw @bef9a3f7@ dcw @c67178f2@ * 8 initial hash values for SHA-256 h0init dcw @6a09e667@ h1init dcw @bb67ae85@ h2init dcw @3c6ef372@ h3init dcw @a54ff53a@ h4init dcw @510e527f@ h5init dcw @9b05688c@ h6init dcw @1f83d9ab@ h7init dcw @5be0cd19@ input0 equ h7init+64 org h7init+65 dc @80000000000000000000000000000000@ input dc @00000000000000000000000000000100@ * 512 bits with the mostly-zero padding end start </code>
Исполняемая программа была нанесена на 85 перфокарт (их вы уже видели в начале статьи). Я также сделал перфокарту с вводом хэш-алгоритма. Для того чтобы запустить программу, мне пришлось загрузить перфокарту в кардридер и нажать кнопку «Загрузка» («Load»). Кардридер обрабатывал по 800 карт в минуту. Таким образом, на загрузку программы ушло всего несколько секунд. Во время выполнения программы консоль компьютера (см. приведенную ниже иллюстрацию) лихорадочно мигала в течение 40 секунд. Наконец, принтер распечатал для меня итоговый хэш (распечатку вы также видели в начале статьи), и результаты были нанесены на новую перфокарту. Так как майнинг Bitcoin использует двойное хэширование SHA-256, процесс хэширования майнинга занял в два раза больше времени (80 секунд).

Усердная работа консоли IBM 1401 во время расчета хэша SHA-256
Сравнение производительности
ЭВМ IBM 1401 может вычислить двойной хэш SHA-256 за 80 секунд. На выполнение данной задачи компьютер потребляет около 3000 Вт мощности, примерно столько же сколько электроплита или сушилка для белья. В свое время базовая система IBM 1401 стоила 125600 долларов США. В реалиях 2015 года это составляет около миллиона долларов США. В то же время, сейчас вы можете купить USB флешку для майнинга за 50 долларов США, в которой имеется специализированная интегральная схема (ASIC USB майнер). Этот USB майнер выполняет 3,6 млрд. хэшей в секунду, потребляя при этом около 4 Вт.
Столь значительные показатели производительности обусловлены несколькими факторами: резким увеличением производительности компьютеров за последние 50 лет согласно закону Мура, потерей производительности, связанной с использованием десятичной арифметики в ЭВМ для решения коммерческих задач, которая была занята вычислением бинарного хэш-кода, а также выигрышем в быстродействии со стороны традиционного аппаратного обеспечения для майнинга биткоинов.
Подведем итоги. Для майнинга блока с учетом текущих требований к данному процессу, ЭВМ IBM 1401 понадобится около 5x10^14 лет (что в 40 000 раз превышает текущий возраст Вселенной). Стоимость израсходованной электроэнергии составит около 10^18 долларов США. В итоге Вы получите 25 биткоинов, чья стоимость в денежном выражении составит около 6000 долларов США. Итак, майнинг биткоинов на мэйнфрейме IBM 1401 прибыльным занятием не назовешь. На приведенных ниже фотографиях сравниваются компьютерные микросхемы 60-х годов прошлого века и современные варианты, наглядно демонстрируя технологический прогресс.


Слева: SMS карты, использовавшиеся в IBM 1401. Каждая карта состоит из множества компонентов с микросхемой. Количество таких карт в компьютере превышало тысячу. Справа: чип Bitfury ASIC позволяет майнить биткоины со скоростью 2-3 гигахэша в секунду. Источник фотографии: zeptobars (CC BY 3.0)
Передача данных по сети
Вы можете решить, что биткоины несовместимы с технологиями 60-х годов прошлого века из-за отсутствия возможности передачи данных по сети. Понадобится ли кому-то пересылать перфокарты с блочной цепью на другие компьютеры? Общение между компьютерами посредством сети появилось достаточно давно. Еще в 1941 году IBM поддерживала так называемый процесс телеметрической (дистанционной) обработки данных. В 60-е годы IBM 1401 можно было подключить к устройству передачи данных IBM 1009 (IBM 1009 Data Transmission Unit) — модему размером с посудомоечную машину, который позволял компьютерам обмениваться друг с другом данными по телефонной линии со скоростью до 300 символов в секунду. То есть, теоретически построение сети Bitcoin на базе технологий 60-х годов прошлого века вполне возможно. К сожалению, мне не удалось заполучить оборудование для телеобработки данных и проверить эту теорию.

Устройство передачи данных IBM 1009. Модем размером с посудомоечную машину появился в 1960 году. С его помощью можно было передавать до 300 символов в секунду по телефонной линии. Источник фотографии: Введение в системы обработки данных IBM Introduction to IBM Data Processing Systems).
Выводы
Использование SHA-256 в ассемблерном языке древнего мэйнфрейма стало непростым, но интересным опытом. Я ожидал более высокой производительности (даже по сравнению с моим множеством Мандельброта за 12 минут). Десятичная арифметика коммерческого компьютера это не лучший вариант для бинарного алгоритма наподобие SHA-256. Однако алгоритм майнинга биткоинов может быть выполнен даже на компьютере без интегральных микросхем. Поэтому, если вдруг некий временной коллапс перенесет меня в 1960 год, я смогу построить сеть Bitcoin.
Музей компьютерной истории в Маунтин-Вью по средам и субботам демонстрирует работающий IBM 1401. Если Вы случайно окажетесь неподалеку, Вам определенно стоит на это взглянуть, сверившись с расписанием работы. А если Вы расскажете сотрудникам музея, которые демонстрируют работающий IBM 1401 обо мне, возможно, они даже запустят мою программу Pi program.
Я хочу выразить благодарность Музею компьютерной истории (Computer History Museum) и членам команды по восстановлению ЭВМ 1401: Роберту Гарнеру, Эду Тэлену, Ван Снайдеру и, в особенности, Стэну Пэддоку. На веб-сайте этой команды ibm-1401.info много интересной информации об ЭВМ 1401 и работе по ее восстановлению.
Разъяснение
Стоит отметить, что я не смайнил реальный блок на IBM 1401 — Музею компьютерной истории это бы не понравилось. Как я уже говорил, имея рабочий IBM 1401, на майнинге заработать не удастся. Однако мне удалось внедрить и выполнить алгоритм SHA-256 на машине IBM 1401, доказав таким образом, что майнинг теоретически возможен. И открою секрет нахождения валидного хэша – я просто использовал уже смайненный блок.
Надеемся, наш перевод вам понравился

Источник: geektimes.ru/company/hashflare/blog/252092/
Портал БАШНЯ. Копирование, Перепечатка возможна при указании активной ссылки на данную страницу.



































