1261
Bitcoin Mining 55-year veteran of IBM 1401
Inspired by the publication habrapolzovatelya mark_ablov « Mein Bitcoin via pen and paper », we decided that readers will giktaym wondering what other crazy ideas able to realize the author of the original post - Ken Shirriffu. i>
Can I use the IBM mainframe comes from the 60s of the last century Mein Bitcoins? I decided to test this, at first glance, a crazy idea. I implemented a hash algorithm Bitcoin in assembly code for the IBM 1401 and tested in practice by running it on a workable model of this ancient mainframe.

Card, which is calculated using the SHA-256 hashes on the mainframe IBM punched card 1401.Za visible printing on the printer, showing the input of the algorithm and the resulting hash i>
As it turned out, with the help of the computer can be Main, but the process takes so long that even the lifetime of the universe may not be enough for a successful single block of mining.
While modern hardware allows to calculate hashes billions per second, the computer in 1401 spends 80 seconds to compute a single hash. Progress performance of computers over the past decade there that clearly described Moore's Law.
Punch cards, participated in the experiment, as well as printing SHA-256 line printer shown in the photos (the first card is a beauty - it was not easy to break this pattern). Note that the second line ends with a group of zeros; This means a successful hash.
The principle of the system of mining Bitcoin
In recent years, electronic currency Bitcoin (Bitcoin), which Internet users can send each other, is very popular. To understand the essence Current cryptocurrency, Bitcoin system can be represented in the form of a log book in which a record of the owners of digital coins (Bitcoin) and the number of coins that he / she has. Buyers Bitcoin can transmit digital coin each other.
It should be noted that the system Bitcoin decentralized: it does not have a single regulatory server, which would follow the course of the transaction. Instead, we are distributing the records of a distributed network of thousands of computers on the Internet.
The difficulty lies in the fact that such a distribution system must somehow ensure that the consent of all users on the records. That is bona fide users should confirm the validity of a transaction, approve it, in spite of the possible presence of scammers and slowly working your network. The solution to this problem was the so-called "mining". About every 10 minutes during the outgoing unit of mining confirmed the transaction, as a result, he is considered to be officially confirmed.
The process of mining, based on a robust cryptography, is extremely difficult, so that no one can control exactly which transactions are mining. In particular, the key idea of Bitcoin is that the result of complex and difficult to obtain, but it is easy to check. This is the so-called technology «proof-of-work» («proof of work»).
The process of mining block requires an enormous amount of computing costs. However, after the unit has been certified, the users peer network can easily verify its validity. The complexity of mining prevents fraudulent use of Bitcoin, and ease of verification unit allows users to be confident in the validity of the transaction.
A side effect of mining is adding new Bitcoin system. Currently, anyone who confirmed the unit receives a 25 generated Bitcoin (now the cost of the number of virtual coins in traditional monetary terms is about 6 thousand. USD). This promotion encourages "miners" to work hard and spend its resources on mining. Given the available opportunity to get to 6 th. US dollars every 10 minutes, mining represented a real "gold mine", encouraging users to spend significant sums on hardware for of mining.

line printer and IBM mainframe in 1401, presented in the exposition of the Computer History Museum (Computer History Museum). This computer is running my program. The console is located at the top left. Black rectangular panel on the computer is a "door" racks that recline, allowing access for maintenance. I>
The process of mining extremely difficult, but the result is very easy to check. The Bitcoin Mining uses cryptography hash function, called SHA-256 double. Hash portion takes the input data and reduces it to a smaller hash value (in this case 256 bit).
A cryptographic hashing algorithm will not yield the desired hash value without exhausting the weight of the input data. However, after the entry is found, which gives the desired value, one can easily check the hash. Consequently, a cryptographic hash is a good way of the «proof-of-work» Bitcoin.
In more detail, in order to smaynit unit must first collect a new block transaction. Then it is necessary to produce a hash block to produce (essentially random way) hash value of the block. If the hash value begins with 16 zeroes, the block is deemed to have confirmed and sent to the network Bitcoin. Most of the time a hash is not successful, so you slightly change the unit and try again and again, spending more than one billion computing operations. About every 10 minutes, someone can successfully confirm the unit and the process begins anew. This is reminiscent of the lottery, which involves miners, attempting for the attempt, as long as someone does not become a "winner." The complexity of the hashing process is difficult visual presentation: it is easier to find a grain of sand in the whole of Earth sand than finding the valid hash value. To find these hash values miners use data centers equipped with special hardware for of mining.
Many explanations for this article, I deliberately simplified. If you want to learn more about the system and Bitcoin mining, I advise to study my articles Difficult Bitcoin mining experience and harsh lessons of mining Bitcoins . < br />
The hash algorithm SHA-256 is used Bitcoin
Now I will discuss hashing function used Bitcoin, which is based on standard cryptographic hash function, called SHA-256. The system uses Bitcoin "double SHA-256." This means that the function SHA-256 is performed twice. SHA-256 algorithm is so simple that it can perform literally being available only pencil and paper , and this algorithm allows you to mix data in unpredictable ways. The algorithm takes as input blocks of 64 bytes, cryptographically processes the data and outputs the 256 bit (32 byte) encrypted data. The algorithm uses a single round, which is repeated 64 times. The illustration below shows one round of an algorithm that takes eight 4-byte blocks, and through H, performs several operations and provides new values for A through H.
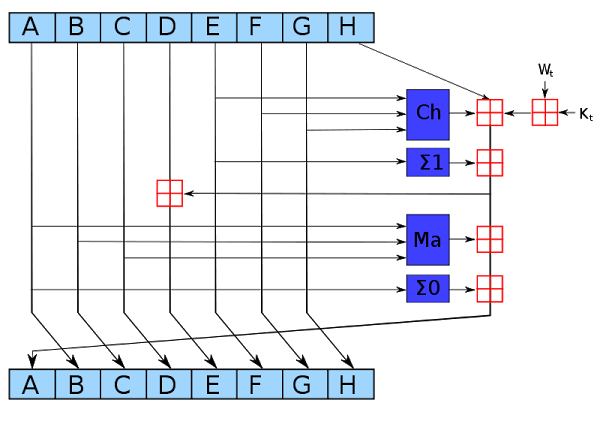
Round SHA-256, as an example illustration of the Wikipedia, Author kockmeyer, CC BY-SA 3.0 i>
Dark blue blocks stirred bits nonlinear manner that is challenging for cryptanalysis. (If you can find a faster way to mathematically produce successful hashes, you can control the mining Bitcoins). Cell Ch «selection" selects the bits of F or G, based on the values of the input cells E. Σ «sum" bits rotated A (or E) generating three cyclic shifted version, and then adds them together modulo 2.
Cell Ma «majority" check bits in each position A, B, and C, and selects 0 or 1, depending on what value is in the majority. Red cells carry a 32-bit addition in generating new value for A and E. Log Wt based on slightly processed input data. (This is where the input block is entered into the algorithm.) Log Kt is a constant determined for each round.
According to the above illustration, a round change only A and E. The remaining values are passed unchanged. The old value of A becomes the new value B, the old value of B becomes the new value of C, and so on. While each round of SHA-256 slightly changes the data after 64 rounds the input data is completely mixed, giving unpredictable output hash value.
IBM 1401
I decided to run the algorithm on a mainframe computer IBM 1401. It appeared in 1959 and by the mid 60s became the best-selling computer - while actively exploited by more than 10 thousand cars. Computers in 1401 was not very powerful computer, even for 1960. However, it was affordable for medium-sized companies that previously could not afford to have a computer, because it can be rented for a small amount of money - $ 2,500 per month.
The IBM 1401 is not used silicon chip. Furthermore, in this computer there were no chips. Its transistors were built on semiconductors germanium crystals, which were used to silicon. Transistors, along with the other components were installed on board the size of a playing card, called SMS card . The computer were used thousands of cards that have been installed in a rack called "door". At IBM in 1401 and twenty of these "doors", which were put forward for the maintenance of your computer. In the illustration seen one open door that provides access to the chips and cables.

The illustration shows an open rack (so-called "door") mainframe IBM 1401. The photo seen SMS card, connected to the circuit. This stance runs Tape i>
The working principle of such a computer is significantly different from modern PCs. In this computer is not used 8-bit bytes and 6-bit code on the basis of binary-coded decimal (BCD). Since this machine was a calculating machine to solve economic problems, it used the decimal rather than binary arithmetic, and every character in the memory has a numeric value from 0 to 9. The memory computer magnetic core housed 4,000 characters. The memory expansion module the size of a dishwasher, increased memory capacity of 12,000 characters. Entering data into a computer implemented with the help of perforated cards. The data and programs read out from the card in card reader. Outgoing data is printed sewage printer speed or their way on maps.
Computer History Museum Computer History Museum in Mountain View has two operable mainframe IBM 1401. On one of them I ran the hash SHA -256. For more information about IBM in 1401 I tell in his article on Fractals IBM 1401
.
Implementation of SHA-256 for IBM 1401
Surely IBM mainframe in 1401 is the worst of all machines that we could choose to run the hash algorithm SHA-256. For effective operation of this algorithm is needed machines that can perform bitwise operations on 32-bit words. Unfortunately, IBM 1401 does not support any 32-bit words or bytes. This computer works with 6-bit characters and does not allow bit operations. Furthermore, it rather binary, decimal arithmetic used. Therefore, the algorithm on a computer in 1401 will be slow and inconvenient to the user.
I ended up using one character for a bit. 32-bit value is stored as 32 characters, or a "0" or "1". My code was supposed to perform character-bit operations, addition and multiplication, checking each character, and deciding what to do with it. As might be expected, the performance of the code took a long time.
Following are written by me assembly code. The whole principle of the code is described in the comments. At the end of the code there is a table of constants required algorithm SHA-256 in hexadecimal. Since 1401 computer does not support hexadecimal format, I had to write their own routines to convert hexadecimal and binary formats. In this article I will not give an explanation of assembler code IBM 1401 only emphasize that it is quite different from that used modern computers. This code does not cause the subroutine, and does not produce results. Due to the lack of general purpose registers is carried out in memory.
Code look under the spoiler:
Hidden Text
Can I use the IBM mainframe comes from the 60s of the last century Mein Bitcoins? I decided to test this, at first glance, a crazy idea. I implemented a hash algorithm Bitcoin in assembly code for the IBM 1401 and tested in practice by running it on a workable model of this ancient mainframe.

Card, which is calculated using the SHA-256 hashes on the mainframe IBM punched card 1401.Za visible printing on the printer, showing the input of the algorithm and the resulting hash i>
As it turned out, with the help of the computer can be Main, but the process takes so long that even the lifetime of the universe may not be enough for a successful single block of mining.
While modern hardware allows to calculate hashes billions per second, the computer in 1401 spends 80 seconds to compute a single hash. Progress performance of computers over the past decade there that clearly described Moore's Law.
Punch cards, participated in the experiment, as well as printing SHA-256 line printer shown in the photos (the first card is a beauty - it was not easy to break this pattern). Note that the second line ends with a group of zeros; This means a successful hash.
The principle of the system of mining Bitcoin
In recent years, electronic currency Bitcoin (Bitcoin), which Internet users can send each other, is very popular. To understand the essence Current cryptocurrency, Bitcoin system can be represented in the form of a log book in which a record of the owners of digital coins (Bitcoin) and the number of coins that he / she has. Buyers Bitcoin can transmit digital coin each other.
It should be noted that the system Bitcoin decentralized: it does not have a single regulatory server, which would follow the course of the transaction. Instead, we are distributing the records of a distributed network of thousands of computers on the Internet.
The difficulty lies in the fact that such a distribution system must somehow ensure that the consent of all users on the records. That is bona fide users should confirm the validity of a transaction, approve it, in spite of the possible presence of scammers and slowly working your network. The solution to this problem was the so-called "mining". About every 10 minutes during the outgoing unit of mining confirmed the transaction, as a result, he is considered to be officially confirmed.
The process of mining, based on a robust cryptography, is extremely difficult, so that no one can control exactly which transactions are mining. In particular, the key idea of Bitcoin is that the result of complex and difficult to obtain, but it is easy to check. This is the so-called technology «proof-of-work» («proof of work»).
The process of mining block requires an enormous amount of computing costs. However, after the unit has been certified, the users peer network can easily verify its validity. The complexity of mining prevents fraudulent use of Bitcoin, and ease of verification unit allows users to be confident in the validity of the transaction.
A side effect of mining is adding new Bitcoin system. Currently, anyone who confirmed the unit receives a 25 generated Bitcoin (now the cost of the number of virtual coins in traditional monetary terms is about 6 thousand. USD). This promotion encourages "miners" to work hard and spend its resources on mining. Given the available opportunity to get to 6 th. US dollars every 10 minutes, mining represented a real "gold mine", encouraging users to spend significant sums on hardware for of mining.

line printer and IBM mainframe in 1401, presented in the exposition of the Computer History Museum (Computer History Museum). This computer is running my program. The console is located at the top left. Black rectangular panel on the computer is a "door" racks that recline, allowing access for maintenance. I>
The process of mining extremely difficult, but the result is very easy to check. The Bitcoin Mining uses cryptography hash function, called SHA-256 double. Hash portion takes the input data and reduces it to a smaller hash value (in this case 256 bit).
A cryptographic hashing algorithm will not yield the desired hash value without exhausting the weight of the input data. However, after the entry is found, which gives the desired value, one can easily check the hash. Consequently, a cryptographic hash is a good way of the «proof-of-work» Bitcoin.
In more detail, in order to smaynit unit must first collect a new block transaction. Then it is necessary to produce a hash block to produce (essentially random way) hash value of the block. If the hash value begins with 16 zeroes, the block is deemed to have confirmed and sent to the network Bitcoin. Most of the time a hash is not successful, so you slightly change the unit and try again and again, spending more than one billion computing operations. About every 10 minutes, someone can successfully confirm the unit and the process begins anew. This is reminiscent of the lottery, which involves miners, attempting for the attempt, as long as someone does not become a "winner." The complexity of the hashing process is difficult visual presentation: it is easier to find a grain of sand in the whole of Earth sand than finding the valid hash value. To find these hash values miners use data centers equipped with special hardware for of mining.
Many explanations for this article, I deliberately simplified. If you want to learn more about the system and Bitcoin mining, I advise to study my articles Difficult Bitcoin mining experience and harsh lessons of mining Bitcoins . < br />
The hash algorithm SHA-256 is used Bitcoin
Now I will discuss hashing function used Bitcoin, which is based on standard cryptographic hash function, called SHA-256. The system uses Bitcoin "double SHA-256." This means that the function SHA-256 is performed twice. SHA-256 algorithm is so simple that it can perform literally being available only pencil and paper , and this algorithm allows you to mix data in unpredictable ways. The algorithm takes as input blocks of 64 bytes, cryptographically processes the data and outputs the 256 bit (32 byte) encrypted data. The algorithm uses a single round, which is repeated 64 times. The illustration below shows one round of an algorithm that takes eight 4-byte blocks, and through H, performs several operations and provides new values for A through H.

Round SHA-256, as an example illustration of the Wikipedia, Author kockmeyer, CC BY-SA 3.0 i>
Dark blue blocks stirred bits nonlinear manner that is challenging for cryptanalysis. (If you can find a faster way to mathematically produce successful hashes, you can control the mining Bitcoins). Cell Ch «selection" selects the bits of F or G, based on the values of the input cells E. Σ «sum" bits rotated A (or E) generating three cyclic shifted version, and then adds them together modulo 2.
Cell Ma «majority" check bits in each position A, B, and C, and selects 0 or 1, depending on what value is in the majority. Red cells carry a 32-bit addition in generating new value for A and E. Log Wt based on slightly processed input data. (This is where the input block is entered into the algorithm.) Log Kt is a constant determined for each round.
According to the above illustration, a round change only A and E. The remaining values are passed unchanged. The old value of A becomes the new value B, the old value of B becomes the new value of C, and so on. While each round of SHA-256 slightly changes the data after 64 rounds the input data is completely mixed, giving unpredictable output hash value.
IBM 1401
I decided to run the algorithm on a mainframe computer IBM 1401. It appeared in 1959 and by the mid 60s became the best-selling computer - while actively exploited by more than 10 thousand cars. Computers in 1401 was not very powerful computer, even for 1960. However, it was affordable for medium-sized companies that previously could not afford to have a computer, because it can be rented for a small amount of money - $ 2,500 per month.
The IBM 1401 is not used silicon chip. Furthermore, in this computer there were no chips. Its transistors were built on semiconductors germanium crystals, which were used to silicon. Transistors, along with the other components were installed on board the size of a playing card, called SMS card . The computer were used thousands of cards that have been installed in a rack called "door". At IBM in 1401 and twenty of these "doors", which were put forward for the maintenance of your computer. In the illustration seen one open door that provides access to the chips and cables.

The illustration shows an open rack (so-called "door") mainframe IBM 1401. The photo seen SMS card, connected to the circuit. This stance runs Tape i>
The working principle of such a computer is significantly different from modern PCs. In this computer is not used 8-bit bytes and 6-bit code on the basis of binary-coded decimal (BCD). Since this machine was a calculating machine to solve economic problems, it used the decimal rather than binary arithmetic, and every character in the memory has a numeric value from 0 to 9. The memory computer magnetic core housed 4,000 characters. The memory expansion module the size of a dishwasher, increased memory capacity of 12,000 characters. Entering data into a computer implemented with the help of perforated cards. The data and programs read out from the card in card reader. Outgoing data is printed sewage printer speed or their way on maps.
Computer History Museum Computer History Museum in Mountain View has two operable mainframe IBM 1401. On one of them I ran the hash SHA -256. For more information about IBM in 1401 I tell in his article on Fractals IBM 1401
.
Implementation of SHA-256 for IBM 1401
Surely IBM mainframe in 1401 is the worst of all machines that we could choose to run the hash algorithm SHA-256. For effective operation of this algorithm is needed machines that can perform bitwise operations on 32-bit words. Unfortunately, IBM 1401 does not support any 32-bit words or bytes. This computer works with 6-bit characters and does not allow bit operations. Furthermore, it rather binary, decimal arithmetic used. Therefore, the algorithm on a computer in 1401 will be slow and inconvenient to the user.
I ended up using one character for a bit. 32-bit value is stored as 32 characters, or a "0" or "1". My code was supposed to perform character-bit operations, addition and multiplication, checking each character, and deciding what to do with it. As might be expected, the performance of the code took a long time.
Following are written by me assembly code. The whole principle of the code is described in the comments. At the end of the code there is a table of constants required algorithm SHA-256 in hexadecimal. Since 1401 computer does not support hexadecimal format, I had to write their own routines to convert hexadecimal and binary formats. In this article I will not give an explanation of assembler code IBM 1401 only emphasize that it is quite different from that used modern computers. This code does not cause the subroutine, and does not produce results. Due to the lack of general purpose registers is carried out in memory.
Code look under the spoiler:
Hidden Text
& lt; code class = & quot; dos & quot; & gt; job bitcoin * SHA-256 hash * Ken Shirriff http://righto.com ctl 6641 org 087 X1 dcw @ 000 @ org 092 X2 dcw @ 000 @ org 097 X3 dcw @ 000 @ org 333 start cs 299 r sw 001 lca 064, input0 mcw 064, 264 w * Initialize word marks on storage mcw + s0, x3 wmloop sw 0 & amp; x3 ma @ 032 @ , x3 c + h7 + 32, x3 bu wmloop mcw + input-127, x3 * Put input into warr [0] to warr [15] mcw + warr, x1 mcw @ 128 @, tobinc b tobin * Compute message schedule array w [0..63] mcw @ 16 @, i * i is word index 16-63 * x1 is start of warr [i-16], ie bit 0 (bit 0 on left, bit 31 on right) mcw + warr, x1 wloop c @ 64 @, i be wloopd * Compute s0 mcw + s0, x2 za +0, 31 & amp; x2 * Zero s0 * Add w [i -15] rightrotate 7 sw 7 & amp; x2 * Wordmark at bit 7 (from left) of s0 a 56 & amp; x1, 31 & amp; x2 * Right shifted: 32 + 31-7 = bit 24 of w [i-15], 31 = end of s0 a 63 & amp; x1, 6 & amp; x2 * Wrapped: 32 + 31 = end of w [i-15], 7-1 = bit 6 of s0 cw 7 & amp; x2 * Clear wordmark * Add w [i-15] rightrotate 18 sw 18 & amp; x2 * Wordmark at bit 18 (from left) of s0 a 45 & amp; x1, 31 & amp; x2 * Right shifted: 32 + 31-18 = bit 13 of w [i-15], 31 = end of s0 a 63 & amp; x1, 17 & amp; x2 * Wrapped: 32 + 31 = end of w [i-15], 18-1 = bit 17 of s0 cw 18 & amp; x2 * Clear wordmark * Add w [i-15] rightshift 3 sw 3 & amp; x2 * Wordmark at bit 3 (from left) of s0 a 60 & amp; x1, 31 & amp; x2 * Right shifted: 32 + 31-3 = bit 28 of w [i-15], 31 = end of s0 cw 3 & amp; x2 * Clear wordmark * Convert sum to xor mcw x1, x1tmp mcw + s0 + 31, x1 * x1 = right end of s0 mcw @ 032 @, x2 * Process 32 bits b xor sw s0 * Restore wordmark cleared by xor mcw x1tmp, x1 * Compute s1 mcw + s1, x2 za +0, 31 & amp; x2 * Zero s1 * Add w [i-2] rightrotate 17 sw 17 & amp; x2 * Wordmark at bit 17 (from left) of s1 a 462 & amp; x1, 31 & amp ; x2 * Right shifted: 14 * 32 + 31-17 = bit 14 of w [i-2], 31 = end of s1 a 479 & amp; x1, 16 & amp; x2 * Wrapped: 14 * 32 + 31 = end of w [ i-2], 17-1 = bit 16 of s1 cw 17 & amp; x2 * Clear wordmark * Add w [i-2] rightrotate 19 sw 19 & amp; x2 * Wordmark at bit 19 (from left) of s1 a 460 & amp; x1, 31 & amp; x2 * Right shifted: 14 * 32 + 31-19 = bit 12 of w [i-2], 31 = end of s1 a 479 & amp; x1, 18 & amp; x2 * Wrapped: 14 * 32 + 31 = end of w [i-2], 19-1 = bit 18 of s1 cw 19 & amp; x2 * Clear wordmark * Add w [i-2] rightshift 10 sw 10 & amp; x2 * Wordmark at bit 10 (from left) of s1 a 469 & amp; x1 31 & amp; x2 * Right shifted: 14 * 32 + 31-10 = bit 21 of w [i-2], 31 = end of s1 cw 10 & amp; x2 * Clear wordmark * Convert sum to xor mcw + s1 + 31, x1 * x1 = right end of s1 mcw @ 032 @, x2 * Process 32 bits b xor sw s1 * Restore wordmark cleared by xor * Compute w [i]: = w [i-16] + s0 + w [i-7] + s1 mcw x1tmp, x1 a s1 + 31, s0 + 31 * Add s1 to s0 a 31 & amp; x1, s0 + 31 * Add w [i-16] to s0 a 319 & amp; x1, s0 + 31 * Add 9 * 32 +31 = w [i-7] to s0 * Convert bit sum to a 32-bit sum mcw + s0 + 31, x1 * x1 = right end of s0 mcw @ 032 @, x2 * Process 32 bits b sum sw s0 * Restore wordmark cleared by sum mcw x1tmp, x1 mcw s0 + 31, 543 & amp; x1 * Move s0 to w [i] ma @ 032 @, x1 a +1, i mz @ 0 @, ib wloop x1tmp dcw # 5 * Initialize: Copy hex h0init-h7init into binary h0-h7 wloopd mcw + h0init-7, x3 mcw + h0, x1 mcw @ 064 @, tobinc * 8 * 8 hex digits b tobin * Initialize ah from h0-h7 mcw @ 000 @, x1 ilp mcw h0 + 31 & amp; x1, a + 31 & amp; x1 ma @ 032 @, x1 c x1, @ 256 @ bu ilp mcw @ 000 @, bitidx * bitidx = i * 32 = bit index mcw @ 000 @, kidx * kidx = i * 8 = key index * Compute s1 from e mainlp mcw + e, x1 mcw + s1, x2 za +0, 31 & amp; x2 * Zero s1 * Add e rightrotate 6 sw 6 & amp; x2 * Wordmark at bit 6 (from left) of s1 a 25 & amp; x1, 31 & amp; x2 * Right shifted: 31-6 = bit 25 of e, 31 = end of s1 a 31 & amp; x1, 5 & amp; x2 * Wrapped: 31 = end of e, 6-1 = bit 5 of s1 cw 6 & amp; x2 * Clear wordmark * Add e rightrotate 11 sw 11 & amp; x2 * Wordmark at bit 11 (from left) of s1 a 20 & amp; x1, 31 & amp; x2 * Right shifted: 31-11 = bit 20 of e 31 = end of s1 a 31 & amp; x1, 10 & amp; x2 * Wrapped: 31 = end of e, 11-1 = bit 10 of s1 cw 11 & amp; x2 * Clear wordmark * Add e rightrotate 25 sw 25 & amp; x2 * Wordmark at bit 25 (from left) of s1 a 6 & amp; x1, 31 & amp; x2 * Right shifted: 31-25 = bit 6 of e, 31 = end of s1 a 31 & amp; x1, 24 & amp; x2 * Wrapped: 31 = end of e , 25-1 = bit 24 of s1 cw 25 & amp; x2 * Clear wordmark * Convert sum to xor mcw + s1 + 31, x1 * x1 = right end of s1 mcw @ 032 @, x2 * Process 32 bits b xor sw s1 * Restore wordmark cleared by xor * Compute ch: choose function mcw @ 000 @, x1 * x1 is index from 0 to 31 chl c e & amp; x1, @ 0 @ be chzero mn f & amp; x1, ch & amp; x1 * for 1, select f bit b chincr chzero mn g & amp; x1, ch & amp; x1 * for 0, select g bit chincr a +1, x1 mz @ 0 @, x1 c @ 032 @, x1 bu chl * Compute temp1: k [i] + h + S1 + ch + w [i] cs 299 mcw + k-7, x3 * Convert k [i] to binary in temp1 ma kidx, x3 mcw + temp1, x1 mcw @ 008 @, tobinc * 8 hex digits b tobin mcw @
To summarize.
Source: geektimes.ru/company/hashflare/blog/252092/





















