1735
"What is the proof?": Insights from theoretical computer science
Theoretical Computer Science - one of the areas of study at the Department of Mathematical and Informational Technologies Academic University. We are often asked what the theoretical computer science. Theoretical Computer Science - a rapidly growing research field, which includes both fundamental areas: algorithms, computational complexity, cryptography, information theory, coding theory, algorithmic game theory, as well as more applications: artificial intelligence, machine learning, the semantics of programming languages, verification, automatic theorem proving, and more. This article we will review only a small plot, namely describe the unusual approach to the concept of evidence which considers the theoretical computer science.

To explain what kind of evidence will be discussed, consider an example: there is a computer program whose authors argue that the program does something specific (specific examples will be later). The program can be run and get an answer. And how can you make sure that the program does what it is supposed to do? It would be nice if in addition to the response to the program provided evidence that the answer is correct.
Consider a more concrete example, we want to have a program that a bipartite graph is a matching of maximum size, together with proof of its maximum.
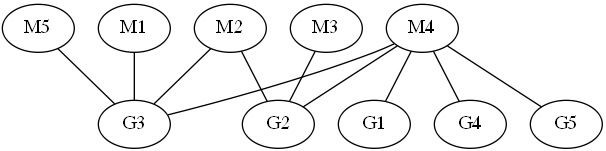
Recall that a graph is called bipartite if its vertices can be colored in two colors so that the edges of the graph connecting vertices of different colors. A matching in a graph is a set of edges that no two of them have a common end. Set of vertices is called a covering if every edge of the graph has at least one end of this set. Koenig theorem states that a bipartite graph matching the size of the maximum coincides with the size of the minimal covering set. Thus, to prove that the maximum matching, can be presented, covering set, whose size matches the size of the matching. Indeed, it covers a lot of will be minimal, since each covering set is required to cover at least one end of each edge of the matching. For example, the graph in Figure matching (M1, G3), (M2, G2), (M4, G1) will be maximized since there is a plurality of size covering 3, which consists of G2, G3, and M4. Note that the check is proof is much easier than to calculate the maximal matching: it is enough to check that the size matching the same size as the covering of the set and check that all the edges are covered.
Consider another example, let's say we need a program that checks the system of non-strict linear inequalities with rational coefficients at the joint (recall that the system of inequalities is called consistent if we can find the values of variables that all inequalities are satisfied).
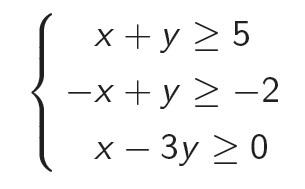
How can you prove the correctness of the result? If the system is consistent, then the proof of consistency can be a solution of the system (it is easy to prove that if such a system is a solution, then there is a rational decision, that it can be written). But how to prove that the system is inconsistent? It turns out that this can be done with the help of the Farkas Lemma, which states that if the system is non-strict linear inequalities is inconsistent, then you can add these inequalities with non-negative coefficients and obtain the contradictory inequality 0≥1. For example, the system is inconsistent in the figure, and if you add the first equation by a factor of 1, the second by a factor of 2, and the third by a factor of 1, you get 0≥1. Proof of inconsistency is just a set of non-negative coefficients.
In this article we will talk about whether or not the evidence or verification of evidence is not always easier than an independent solution of the problem. (In the example of the maximal matching, we have not shown that there is no algorithm that solves the problem in the same time, how long it takes checks proof.) If we do not limit the size of the evidence, it would appear that the evidence needed, and if we require that the evidence was correct, the question of the usefulness of evidence equivalent to an important discovery on the equality of classes P and NP. Then we'll talk about interactive proofs (proof in the dialog). Discuss cryptographic proof that not disclose too much information, except loyalty proves the assertion. And ended with a discussion of probabilistic verifiable evidence and PCP-famous theorem, which is used to prove the difficulty of approximation of optimization problems.
In this article, we will not deal with automated theorem proving and proving the correctness of programs, although these themes are also quite interesting.
Do you need proof? H4>
Short proof h4>

To explain what kind of evidence will be discussed, consider an example: there is a computer program whose authors argue that the program does something specific (specific examples will be later). The program can be run and get an answer. And how can you make sure that the program does what it is supposed to do? It would be nice if in addition to the response to the program provided evidence that the answer is correct.
Consider a more concrete example, we want to have a program that a bipartite graph is a matching of maximum size, together with proof of its maximum.

Recall that a graph is called bipartite if its vertices can be colored in two colors so that the edges of the graph connecting vertices of different colors. A matching in a graph is a set of edges that no two of them have a common end. Set of vertices is called a covering if every edge of the graph has at least one end of this set. Koenig theorem states that a bipartite graph matching the size of the maximum coincides with the size of the minimal covering set. Thus, to prove that the maximum matching, can be presented, covering set, whose size matches the size of the matching. Indeed, it covers a lot of will be minimal, since each covering set is required to cover at least one end of each edge of the matching. For example, the graph in Figure matching (M1, G3), (M2, G2), (M4, G1) will be maximized since there is a plurality of size covering 3, which consists of G2, G3, and M4. Note that the check is proof is much easier than to calculate the maximal matching: it is enough to check that the size matching the same size as the covering of the set and check that all the edges are covered.
Consider another example, let's say we need a program that checks the system of non-strict linear inequalities with rational coefficients at the joint (recall that the system of inequalities is called consistent if we can find the values of variables that all inequalities are satisfied).
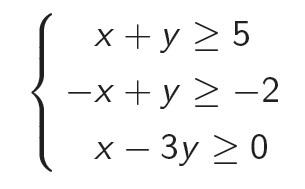
How can you prove the correctness of the result? If the system is consistent, then the proof of consistency can be a solution of the system (it is easy to prove that if such a system is a solution, then there is a rational decision, that it can be written). But how to prove that the system is inconsistent? It turns out that this can be done with the help of the Farkas Lemma, which states that if the system is non-strict linear inequalities is inconsistent, then you can add these inequalities with non-negative coefficients and obtain the contradictory inequality 0≥1. For example, the system is inconsistent in the figure, and if you add the first equation by a factor of 1, the second by a factor of 2, and the third by a factor of 1, you get 0≥1. Proof of inconsistency is just a set of non-negative coefficients.
In this article we will talk about whether or not the evidence or verification of evidence is not always easier than an independent solution of the problem. (In the example of the maximal matching, we have not shown that there is no algorithm that solves the problem in the same time, how long it takes checks proof.) If we do not limit the size of the evidence, it would appear that the evidence needed, and if we require that the evidence was correct, the question of the usefulness of evidence equivalent to an important discovery on the equality of classes P and NP. Then we'll talk about interactive proofs (proof in the dialog). Discuss cryptographic proof that not disclose too much information, except loyalty proves the assertion. And ended with a discussion of probabilistic verifiable evidence and PCP-famous theorem, which is used to prove the difficulty of approximation of optimization problems.
In this article, we will not deal with automated theorem proving and proving the correctness of programs, although these themes are also quite interesting.
Do you need proof? H4>
Language is the set of strings over some finite alphabet. In theoretical computer science is usually considered evidence of statements of the form x∈L, where L - language and x - some string. Approval of this type of mathematical theorems generalize, as any mathematical theorem states that statement, written in a formal language, belongs to the set of true statements.
Proof system for a language L is called an algorithm A (x, w), which takes as input two lines: x and w and checks that the string w is evidence accessories x∈L. From the proof system requires two properties: the correctness and completeness. Correctness states that if for some strings x and w algorithm A (x, w) gives 1, the x∈L. Completeness states that for each x∈L there exists a string w, the algorithm A (x, w) issue 1.
Languages for which there is proof system, called enumerable languages. If you are faced with a different definition of the enumerated language, as an exercise, prove their equivalence.
Language L is called solvable if there exists an algorithm B, which when x∈L algorithm B (x) outputs 1 and at x∉L return 0. Any soluble language has a system of evidence, proof of which is empty. A natural question, is it required that for any language for which there is evidence of the system, and there is a decision algorithm. The answer to this question is known, there are languages for which there is evidence of the system, but for which there is no deciding algorithm. Come up with some kind of an example of such a language is not difficult, more difficult to come up with a natural example. Consider the language, which consists of polynomials with integer coefficients on many variables, which vanish at least for some integer variables. Proof system for this language is constructed simply, the proof will be integer variables, in which the polynomial vanishes. DPRM-theorem (named after the author: Davis, Putnam, and Robinson Matiyaesevich) argues that this language is not solvable, ie, there is no algorithm that checks whether a polynomial is drawn to zero at integer points. The last step in the proof of this theorem by Academician V. Matijasevic and this theorem gives a negative answer to the 10th problem of Hilbert.
Short proof h4>
While we do not impose any restrictions on the algorithm that checks the size of the proof and evidence. Will there be a useful proof of the correctness of the result of a program, if the time required to verify proof of more than execute the program? It seems that such evidence is meaningless, so we will require that the algorithm A (x, w) in the definition of evidence would work polynomial in the length of x, and the length of time w proof, such proof system will be called effective.

We say that a language L belongs to NP, if it has an efficient system of evidence and a polynomial p, such that for any x∈L there is evidence accessories x∈L length not greater than p (| x |). Language L belongs to the class P, if there is a polynomial-time algorithm that determines if the input string language L. The class P is contained in the class NP, since for each language L of P, the algorithm determines if L, and he will be a system of evidence, if it is assumed that it ignores the proof. At this point it is not known whether there are languages in the class NP, which do not belong to the class P. The question of the P versus NP problem is included in the list of the seven millennium problems, compiled by the Institute of Clay; for the solution of this problem announced a prize of one million dollars. Many have heard about the list of tasks Goals in connection with the proof of the Poincare conjecture GY Perelman. Most experts believe that the classes P and NP are not equal.
Consider the examples of languages in the class NP:
- Language composite numbers is in the class NP. To prove that the number n of the compound is sufficient to produce two integers a and b, which is greater than one and n = ab. Language primes also belongs to the class NP, but it is more difficult to prove. However, in 2002, Kayal and Saxena proved that the language simple (and, consequently, and composite) numbers belongs to the class P.
- Consider the language GI, which consists of a pair of isomorphic graphs. We believe that the vertices of the graph are numbered from 1 to n, each
edge connects exactly one pair of vertices. Two graphs G 1 sub> (V 1 sub>, E 1 sub>) and G 2 sub> (V 2 sub>, E 2 sub>) are called isomorphic if the vertices of the first graph can be renumbered so that the first graph has become the same as the second column. This means that after renumbering the first set of edges of the graph will coincide with the second set of edges of the graph. Language GI belongs to the class NP, proof of isomorphic graphs will permutation of the vertices of the first graph, which gives an isomorphism. Lying Tongue GI in class P, is an open question. Consider also the language of GNI, which consists of pairs of nonisomorphic graphs on the same number of vertices. About GNI language is unknown whether he is in NP, since it is not clear how short to prove that two graphs are isomorphic.
- Consider the language HamPath, which consists of graphs in which there is a Hamiltonian path, ie, such a way that exactly once through each vertex. This language is in the class of NP, because as evidence of possible ways to use the path itself. About the language is not known whether he in the class P, but it is known that it is NP-complete. The latter in particular means that HamPath is not in P, if P ≠ NP. Addition HamPath language coincides with the set of graphs in which there is no Hamiltonian path. Lies in whether the addition HamPath class NP is unknown.
Interactive proofs h4>
So far, the evidence that we considered to be very similar to the familiar us, namely, the proof - is some text which, although it is not clear how to invent, but is easy to check if there is an algorithm that checks the validity of the evidence. That is, to come up with proof you need to have any special abilities, and everyone can check the proof. In fact, not all the evidence of modern mathematics have this property. Firstly, the evidence does not write on an easy to automatically check the formal language, and secondly, to understand the evidence in some areas, it is necessary to spend a few years in the study of this area.
In mathematical circles for pupils often practiced this format classes: children given a set of tasks when the child believes he solved the problem, he says the decision orally teacher. And going dialogue between teacher and pupil, who convinces the teacher or that the problem is solved or not convinced.
Consider the example of an interactive proof: a program that solves the problem of graph isomorphism. In the case where the graphs are isomorphic, the program can prove the correctness of his answer by giving permutation gives an isomorphism. We show how it is possible in a dialogue to show that non-isomorphic graphs. Let the user program asked, whether isomorphic graphs G 0 sub> and G 1 sub> and got the answer that they are isomorphic. The user throws a coin (selects a random element i of the set {0, 1}) and chooses a random permutation of n-element set (with all the permutations are considered equally probable) σ. And asks the program, there are isomorphic graphs G 0 sub>, σ (G i sub>). If i = 0, then the program is expected to answer that graphs are isomorphic, and if i = 1, then the program is expected that the graphs are not isomorphic. If the graph G 0 sub> and G 1 sub> were indeed isomorphic, then the program can easily give the right answer to this question. And if G 0 sub> and G 1 sub> are isomorphic, then the graph of σ (G i sub>) is equally likely to be a permutation of G 0 sub>, and permutation of G 1 sub>, so the program will give the expected answer with a probability greater than 1/2. The probability of error can be reduced by repeating the algorithm n times and decide that the algorithm works correctly if each of the n runs has been given the right answer; the probability of error in this case does not exceed 1/2 n sup>.
In the above example, the proof only that - it is a dialogue between proves (program) and inspection (by the user), while proving can be arranged very difficult, and the verifier can only do simple things (to produce a polynomial-time computation). If the item x∈L, proving that with probability 1 must convince the examiner, and if x∉L, then the verifier must take such evidence with probability no greater than 1/10. Theorem Shamir argues that such interactive proof system with short dialogues exist for all languages L, for which there is recognition algorithm using polynomial memory. In particular, we can in polynomial time to prove that the graph has no Hamiltonian path.
Zero-knowledge proof h4>
The concept of evidence is found not only in mathematics and computer science, but also in law. For example, a person accused of a crime, he can prove that he was not at the crime scene, but does not want to disclose where he was in fact (for example, it could be a lover or want to hide your location from the competition). Alibi is not a crime, but his announcement is very undesirable. It turns out that it is theoretically possible to prove so as not to disclose too much information but proves the assertion.
Consider this example: some firms write programs that quickly solve the problem of graph isomorphism, but the free version of this program just says graphs are isomorphic or not giving permutation when the graphs are isomorphic. To obtain a permutation need to buy the paid version of the program. But in the meantime, developers want to enable the user to make sure that the graphs really are isomorphic, but that this information does not help the user to find the isomorphism yourself. This can be done as follows: if the graphs G 0 sub> and G 1 sub> are isomorphic, then you can select a random permutation π and issue a graph G 2 sub> = π ( G 1 sub>), and prompt the user to decide what counts isomorphism he wants to get G 0 sub> and G 2 sub> and G 1 sub> and G 2 sub>. The program will respond exactly to one of these requests. If the program knows isomorphism, then it can easily respond to your request, if there is an isomorphism, then at least one of the options the user's request to issue a response. And if the user will select at random a request, then the probability that the isomorphism between user-selected options are there, does not exceed 1/2. Error can be reduced by repeating this process: choosing a new permutation and prompting the user to select a new option.
It turns out that for each language in the class NP for some cryptographic assumption can construct an interactive proof of belonging, which will not give any information about the classical proof accessories (which exists for any language in the class NP). Said cryptographic assumption - is the existence of one-way functions, ie functions which are easy to compute but hard to turn. For example, many believe that the function that two n bit numbers gives their product is one-sided.
probabilistically verifiable proofs h4>
Let math teacher gives his students homework, they pass him a notebook with the decision. Any teacher of mathematics dreams, so that you can check a decision without reading it completely. Option to check the solution only bad answers, because the answer can be written off or guess, and also it does not help in the tasks for evidence that the responses as such or not.