1817
“什么是证据?”:从理论计算机科学见解
理论计算机科学 - 学习在部门数学和信息技术学术大学的地区之一。我们经常问什么理论计算机科学。理论计算机科学 - 一个快速成长的研究领域,其中既包括基本领域:算法,计算复杂性,密码学,信息论,编码理论,算法博弈论,多应用:人工智能,机器学习,编程语言,验证语义,自动定理证明,等等。本文将专门的一小块审查,即讲述一个不寻常的方式来证明它参考了理论计算机科学的概念。

为了解释什么样的证据进行讨论,考虑一个例子:有一个计算机程序,其作者声称,该计划是做一些具体的事情(具体的例子会更高)。该程序可以运行,并得到了答案。以及如何确保程序做的事情是应该做的?这将是很好,如果除了应对方案提供的证据表明,答案是正确的。
考虑一个具体的例子:我们希望有一个计划,在二分图的最大尺寸的匹配以及其最大的证明。
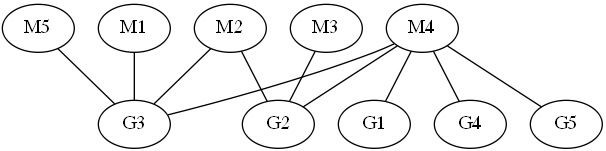
回想一下,一个图是二分如果其顶点可着色两种颜色,以使图的边连接的不同颜色的顶点。在图匹配是一个集边,没有两个人有一个共同的目的。顶点组被称为一个罩,如果图中的每个边缘具有在这组中的至少一个端部。柯尼希定理指出,一个二分图的最大匹配尺寸与最小生成树集的大小一致。因此,要证明一个最大匹配,可呈,覆盖集的大小匹配的尺寸相匹配。的确,它覆盖集将是最小的,因为要求每个覆盖集来覆盖匹配的每个边缘的至少一端上。例如,该曲线图在图匹配(M1,G3),(M 2,G2),(M4,G1),将被最大化,因为有覆盖多个大小为3,它由G2,G3和M4的。应当注意,检验是证明是更容易比来计算最大匹配,足以验证的匹配的大小与该组的覆盖物的大小相一致,检查是否所有的边缘都包括在内。
考虑另一个例子,假设我们需要一个程序,检查不严格的线性不等式与联合有理系数系统(记得不平等的制度被认为是一致的,如果我们能找到的变量,所有的不平等都满意的值)。
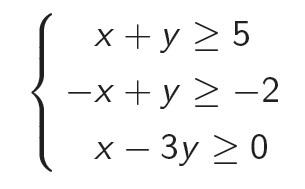
我们如何能证明结果的正确性?如果系统是一致的,则一致性的证据可以是系统中的溶液(它是容易证明,如果这样的系统具有的溶液中,然后有一个合理的解决方案,即它可以被写入)。但如何证明该系统是不一致的?事实证明,这可以通过使用法卡斯引理,其中规定,如果系统是不严格的线性不等式是不一致的完成,那么你就可以用非负系数增加这些不平等和获得相互矛盾的不平等0≥1。例如,该系统在图中是不一致的,并且如果我们添加的第一个方程由图1中,第二个系数以2的因子,第三由1倍,则得到0≥1。不一致的证明只是一组非负系数。
在本文中,我们将讨论有关的证据或试验证据与否并不总是比独立的决策任务更容易。 (在最大匹配的例子中,未示出,没有算法的同时解决该问题,需要多长时间验证的证据)。如果我们不限制证据的大小,看来该证据是必要的,并且如果我们要求的证据证据等同于类P与NP的平等问题的重要发现的有用的正确的,那么这个问题。然后我们来谈谈交互式证明(证明中的对话)。我们讨论了密码的证据,也没有透露不必要的信息,除了忠诚度证明了断言。和结束讨论概率可验证样张和PCP-著名定理,这是用来证明的优化问题的近似的难度。
在本文中,我们将不会处理自动定理证明和方案正确性的证明,虽然这些主题也颇为有趣。
你需要证明吗? H4>
短样张 H4>

为了解释什么样的证据进行讨论,考虑一个例子:有一个计算机程序,其作者声称,该计划是做一些具体的事情(具体的例子会更高)。该程序可以运行,并得到了答案。以及如何确保程序做的事情是应该做的?这将是很好,如果除了应对方案提供的证据表明,答案是正确的。
考虑一个具体的例子:我们希望有一个计划,在二分图的最大尺寸的匹配以及其最大的证明。

回想一下,一个图是二分如果其顶点可着色两种颜色,以使图的边连接的不同颜色的顶点。在图匹配是一个集边,没有两个人有一个共同的目的。顶点组被称为一个罩,如果图中的每个边缘具有在这组中的至少一个端部。柯尼希定理指出,一个二分图的最大匹配尺寸与最小生成树集的大小一致。因此,要证明一个最大匹配,可呈,覆盖集的大小匹配的尺寸相匹配。的确,它覆盖集将是最小的,因为要求每个覆盖集来覆盖匹配的每个边缘的至少一端上。例如,该曲线图在图匹配(M1,G3),(M 2,G2),(M4,G1),将被最大化,因为有覆盖多个大小为3,它由G2,G3和M4的。应当注意,检验是证明是更容易比来计算最大匹配,足以验证的匹配的大小与该组的覆盖物的大小相一致,检查是否所有的边缘都包括在内。
考虑另一个例子,假设我们需要一个程序,检查不严格的线性不等式与联合有理系数系统(记得不平等的制度被认为是一致的,如果我们能找到的变量,所有的不平等都满意的值)。
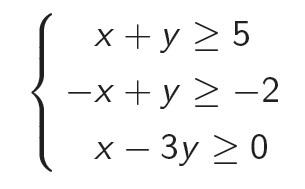
我们如何能证明结果的正确性?如果系统是一致的,则一致性的证据可以是系统中的溶液(它是容易证明,如果这样的系统具有的溶液中,然后有一个合理的解决方案,即它可以被写入)。但如何证明该系统是不一致的?事实证明,这可以通过使用法卡斯引理,其中规定,如果系统是不严格的线性不等式是不一致的完成,那么你就可以用非负系数增加这些不平等和获得相互矛盾的不平等0≥1。例如,该系统在图中是不一致的,并且如果我们添加的第一个方程由图1中,第二个系数以2的因子,第三由1倍,则得到0≥1。不一致的证明只是一组非负系数。
在本文中,我们将讨论有关的证据或试验证据与否并不总是比独立的决策任务更容易。 (在最大匹配的例子中,未示出,没有算法的同时解决该问题,需要多长时间验证的证据)。如果我们不限制证据的大小,看来该证据是必要的,并且如果我们要求的证据证据等同于类P与NP的平等问题的重要发现的有用的正确的,那么这个问题。然后我们来谈谈交互式证明(证明中的对话)。我们讨论了密码的证据,也没有透露不必要的信息,除了忠诚度证明了断言。和结束讨论概率可验证样张和PCP-著名定理,这是用来证明的优化问题的近似的难度。
在本文中,我们将不会处理自动定理证明和方案正确性的证明,虽然这些主题也颇为有趣。
你需要证明吗? H4>
语言是一组对一些有限的字母串。在理论计算机科学通常被认为是形式x∈L,陈述的证据,其中L - 语言和x - 一些字符串。这种数学定理的断言一概而论,因为任何数学定理指出,记录在形式语言的陈述,属于一组真实的陈述。
证明系统的语言L是一个算法A(X,W),这需要输入两行:X和W,并检查一个字符串w是从属关系x∈L的证明。从证明系统需要两个属性:正确性和完整性。正确指出,如果一些字符串X和W算法A(X,W)输出1,然后x∈L。完整的状态,对于每一个存在x∈L串W,算法A(X,W)输出1
语言其中有一个系统,称为枚举语言的证据。如果你面对的是一个不同的定义枚举的语言,作为一个练习,证明自己的等价性。
语言L是可解的,如果有一个算法B,即x∈L算法B(x)的输出1,而x∉L给出0.任何语言是可判定的防爆系统,其证明是空的。一个自然的问题,无论是必需的,对于任何语言的量有一个系统的证据,并且有一个决策算法。在这个问题的答案是已知的,也有语言里面是有系统的证据,但其没有决定的算法。拿出一些例如这样的语言并不困难,更难以拿出一个自然的例子。认为由多项式与消失,至少在某些整数变量的许多变量的整数系数的语言。防爆系统,这种语言构造简单,证明将是整型变量,其中多项式消失。 DPRM定理(命名作者:戴维斯,普特南,罗宾逊和Matiyaesevich)认为,这种语言不是可解,即不存在的算法,用于检查一个多项式是否被吸引到零的整数点。在这个定理院士V. Matijasevic这个定理的证明的最后一步给出了否定的答案,希尔伯特第十问题。
短样张 H4>
虽然我们不强加给它检查的证明和证据的尺寸算法任何限制。会有某些程序的结果的正确性的一个有用的证明,如果所需要的时间,以验证该证据以上的程序的执行?看来这些证据是没有意义的,因此,我们所需要的算法A(X,W)中的证据的定义将工作多项式x的长度和时间瓦特证明的长度,这样的证明系统将被称为有效。

我们说一个语言L属于NP类,如果有证据的有效制度和多项式p,使得对任何证明存在x∈L配件x∈L长度不超过P越大(| X |)。语言L属于类P,如果存在一个多项式时间算法,用于验证的类P被包含在类的NP在LL中的输入字符串的身份,因为对于每个语言L P中,该算法检查身份L,并且他将成为证据的系统中,如果假定它忽视了证明。目前,我们不知道是否有类NP,不属于类P. P的问题与NP问题是包含在七千年的问题,由克莱研究所编制的名单语言;对于这个问题的解决方案是宣布一百万美元的奖金。很多人听说过的任务与庞加莱猜想GY佩雷尔曼的证明千年连接列表。大多数专家认为,类P和NP是不一样的。
考虑从NP类语言的例子:
- 语言合数是类NP。证明充分的化合物的数量n,以产生两个整数a和b,这是大于1且n =从头。语言素数还在于NP类,但它更难以证明。然而,2002年,Kayal和Saxena先生证明,语言简单(因而,复合)的数字是在类P.
- 考虑语言GI,其中包括对同构图形的。我们相信,在图形的顶点编号从1到n,每
正好一个边连接的一对顶点。两个图G 1 SUB>(V 1 SUB>,E 1 SUB>)和G 2 SUB>(V 2 子>中,E <子> 2 分>)被称为同构的,如果第一图的顶点可以被重新编号,使得所述第一图形是相同的第二图表。这意味着,重编所述第一组图形的边缘的后正好与该集合中的第二图表的边缘。语言的GI在于NP类,证明将是第一曲线图中,它定义一个同构的顶点的同构的图形排列。谎言在语言类GI P是否是一个悬而未决的问题。想想也是GNI的语言,其中包括对在顶点相同数量的不同构图形。关于语言GNI未知他是否是NP,因为目前尚不清楚如何简单地证明了两个图是同构的。
- 考虑语言HamPath,其中包括图形,其中有一个汉弥尔顿路径,即,这样一种方式,正好一次经过每个顶点。这种语言是在类NP的,因为随着使用本地路径可能途径的证据。有关此语言是不知道他是否在一类的P,但已知的是它是NP完全问题。特别是后者意味着HamPath不是在P,当P≠NP。补充语言HamPath恰逢集图,其中没有哈密顿路径。在于除了HamPath类NP是否是未知的。
LI> UL>
交互式证明 H4>
到目前为止,我们考虑的证据是非常类似于通常我们,即证明 - 这是某些文本,它们虽然并不清楚如何去发明,但很容易检查,存在一种算法,验证该证据的正确性。那就是拿出你需要有什么特殊能力的证明,并验证证明每个人都可以。事实上,在现代数学并不是所有的证据都具有此属性。首先,该证据不能在一个简单的写为自动检查的形式语言,其次,要了解在某些领域,你需要花费学习这方面的几年证据。
在数学界的学生常练此格式的类:给定的任务,当孩子认为自己解决了这个问题的孩子,他说,这一决定口头老师。并有老师和学生之间的对话,谁说服老师或问题解决或没有说服力。
考虑一个交互式证明的例子:有一个程序,解决了图同构的问题。在该图是同构的情况下,该程序可以证明他的答案的正确性,其给出的置换给出了一个同构。我们展示了对话如何证明图是同构的。让用户要求的程序图是同构当G <分> 0 SUB>和G 1 SUB>,并收到了回信,他们不是同构的。用户抛出一个硬币(从该组中选择一个随机元素i {0,1}),并且选择一个随机置换n元素组(所有排列被认为是同样可能的)σ。并要求计划图是同构当G <分> 0 SUB>,σ(G <分> I SUB>)。若设为i = 0,则程序预计回答这个曲线图是同构的,而若设为i = 1,则程序预计该图不同构。如果图G <分> 0 SUB>和G 1 SUB>确实是同构的,那么毫无困难的方案给出正确的答案。而当G <分> 0 SUB>和G 1 SUB>是同构的,σ那么图(G <分> I SUB>)也同样可能是G的排列<分> 0 SUB>和置换摹 1 SUB>,这样程序会给出的概率大于1/2的预期的答案。误差的概率可通过重复算法的n倍,并决定,该算法可以正常工作,如果每n个游程分别获得了正确的答案被减少;误差在这种情况下的概率不超过1/2 <燮>Ñ功能 sup>。
在上述示例中,唯一的证据 - 它是一个对话之间证明(程序)和检查(由用户),从而证明可安排非常困难的,并且所述检验只能做简单的事情(以产生一个多项式时间计算)。如果x∈L该项目时,证明以概率1应该使检查者,并且如果x∉L,则验证者应当接受这样的证据,以不超过1/10的概率。沙米尔的定理断言,这种交互式证明系统与短对话存在于所有语言L,对其中有利用多项式内存识别算法。特别是,我们可以在多项式时间内,证明该图没有汉弥尔顿路径。
零知识证明 H4>
证据的概念,不仅在数学和计算机科学,而且在法律。例如,被指控犯罪的人,他能证明他不在犯罪现场,但不希望透露,他实际上是(例如,它可能是一个情人或要在竞争中隐藏自己的位置)。不在场证明是不是犯罪,但他的阅读是非常不可取的。原来,这在理论上是可能的,以证明,以便不泄露太多的信息,比所需的断言等。
考虑这个例子:一些企业编写解决快图同构问题的方案,但这个方案的免费版本只是说图是同构与否,给人一种置换时,图是同构的。为了获得一个排列,你需要购买付费版本。但在此期间,开发商想使用户能够确保该图确实是同构的,但这些信息并没有帮助用户找到自己的同构。这是可以做到如下:如果图G <分> 0 SUB>和G 1 SUB>是同构的,那么你可以选择一个随机排列π,并发出一个图G 2 SUB> =π(摹 1 SUB>),并提示用户来决定图形的同构性,他希望得到对G <分> 0 SUB>和G 2 SUB>和G 1 SUB>和G 2 SUB>。该方案将正好回应这些疑问之一。如果程序知道同构,它可以很容易地响应您的请求,如果存在一个同构,则至少有一个用于发出一个响应于用户的请求的内容。并且,如果用户将在随机选择的查询,那么概率是用户可选择的选项之间的同构时,不超过1/2。误差可以通过重复这个过程被减少:选择一个新的置换和提示用户选择一个新的选项
事实证明,在NP类下的一些加密的假设每种语言,人们可以建立属于这样一个互动的证明,这不会给有关从属关系的经典证明(它存在于类NP任何语言)的任何信息。所述加密的假设 - 是单向函数,即存在的函数,它们容易计算,但很难打开。例如,许多人认为,该函数的两个n位数字给他们的产品是片面的。
概率可验证的证据 H4>
让数学老师给他的学生们的功课,他们通过他的决定的笔记本电脑。数学梦想的任何老师,这样你就可以检查该解决方案完全没有阅读它。选项仅由答案,以检验其是坏的,因为答案可以注销或猜测,并且也不会在任务帮助的证据,其中,所述反应为,例如与否。