1750
«Що таке доказ?»: Вид з теоретичної комп’ютерної науки
Теоретико-інформатика — один з напрямків дослідження кафедри математичних та інформаційних технологій ВНЗ. Ми часто запитуємо, що теоретична комп’ютерна наука. Теоретична комп’ютерна наука є активно розвиваючи науковий напрямок, який включає в себе як фундаментальні області: алгоритми, обчислювальна складність, криптографія, теорія інформації, теорія кодування, алгоритмічна теорія гри та інші прикладні: штучний інтелект, машинне навчання, семантика мов програмування, перевірка, автоматичний теоретичний доказ і багато іншого. Ми приведемо цю статтю на огляд тільки невеликої ділянки, а саме, ми будемо говорити про незвичайні підходи до концепції доказів, які розглянуті теоретичні комп'ютерні науки.

Для того, щоб пояснити, які докази ми будемо говорити про, будь ласка, зайдіть приклад: є комп'ютерна програма, автори якої стверджують, що програма робить щось конкретним (специфічні приклади будуть дані пізніше). Ви можете запустити програму і отримати відповідь. Як ви впевнені, що програма, яка повинна робити? Це буде добре, якщо, крім відповіді, програма забезпечить доказ того, що ця відповідь є правильним.
Розглянемо більш конкретний приклад: ми хочемо мати програму, яка знаходить максимальний розмір парі в двосторонньому графі разом з підтвердженням його максимальності.
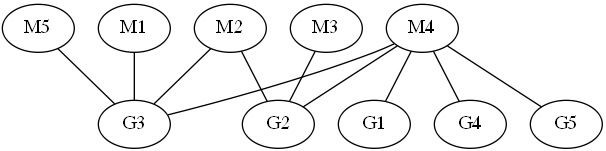
Нагадаємо, що граф називається біпартитом, якщо його вершини можна пофарбувати в два кольори, щоб краю графіка з'єдналися вершини різних кольорів. Парад в графі називається таким набором ребер, які не мають двох з них спільного кінця. Набір вершин графа називається покриттям, якщо кожен край графіка має принаймні один кінець в цьому наборі. теорема Коеніга говорить про те, що в двосторонньому графі розмір максимальної пари збігається з розмірами мінімального комплекту покриття. Таким чином, щоб довести, що відповідність є максимальним, можна пред'явити встановлене покриття розміром якого збігається з розмірами цієї пари. Дійсно, цей набір покриття буде мінімальним, так як кожен набір покриття повинен покрити принаймні один кінець кожного краю цієї пари. Наприклад, в графі на малюнку парування (M1, G3), (M2, G2), (M4, G1) буде максимальним, так як є набір покриття розміром 3, який складається з G2, G3 і M4. Зверніть увагу, що набагато простіше перевірити такий доказ, ніж розрахувати максимальну пару: просто перевірте, що розмір парі збігається з розмірами комплекту покриття і перевірте, що всі ребра вкриті.
Розглянемо ще один приклад, давайте сказати, що нам потрібна програма, яка тестує систему необмежених лінійних нерівностей з раціональними коефіцієнтами сумісності (щодо того, що система нерівностей називається спільним, якщо ви можете знайти такі значення змінних, які всі нерівності будуть виконані).
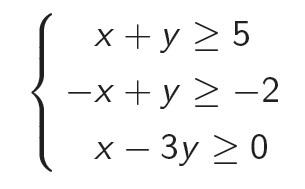
Як можна довести правильність результату? Якщо система кооперативна, то підтвердження співпраці може бути розчином системи (непросто довести, що якщо така система має рішення, то є раціональне рішення, тобто його можна писати). Як ви доведете, що система не сумісна? Виявляється, що це можна зробити за допомогою леймази Farkas, що говорить про те, що якщо система незрівнянних лінійних нерівностей несумісна, то можна додати ці нерівності з ненегативними коефіцієнтами і отримати суперечливу нерівність 0 ≥ 1. Наприклад, система на малюнку несумісна, і якщо додати перше рівняння з коефіцієнтом 1, другий з коефіцієнтом 2, а третій з коефіцієнтом 1, ви отримуєте 0 ≥ 1. Вистоювання несумісних коефіцієнтів буде просто набором негативних коефіцієнтів.
У цій статті ми будемо говорити про те, чи потрібен доказ, чи є перевірка доказів завжди не простіше, ніж рішення проблеми самостійно. (На прикладі максимального узгодження ми не доведемо, що не існує алгоритму, який вирішує проблему одночасно, оскільки це вимагає перевірки доказу.) Якщо ми не обмежуємо розмір доказу, ми знайдемо, що докази необхідно, і якщо ми вимагаємо, що докази будуть правильними, то питання необхідності доказування є еквівалентним найважливішим відкритим питанням рівності класів P і NP. Далі ми будемо говорити про інтерактивні докази. Поговоримо криптографічні докази, які не мають зайвої інформації, окрім правди перевіреної претензії. І ми завершуємо обговорення ймовірних доказів і відомої теореми ПКП, яка використовується для доведення труднощів приблизних задач оптимізації.
У цій статті ми не будемо торкнутися на автоматичний доказ теорем і доказ вірності програм, хоча ці теми також досить цікаві.
Чи потрібна допомога?
Мова - набір ліній над скінченним алфавітом. В теоретичній комп'ютерній науці зазвичай розглядаються докази виписок xaL, де L мова і x є рядком. Заяви такого роду узагальнені математичні теореми, оскільки будь-які математичні теореми, що заява, написана у формальній мові, належить до набору вірних виписок.
Система доказування мови L називається алгоритмом A(x,w), який отримує дві лінії в вході: x і w і перевіряє, що рядок w є доказом належності x,L. Два властивості необхідні для доказової системи: виправлення і повноти. Виправленість стверджує, що якщо для деяких рядків x і w алгоритм A(x,w) виходи 1, потім x,L. Повністю станів, які для кожного x,L є такий рядок, що алгоритм A(x,w) виходи 1.
Мови, для яких існують доказові системи. Якщо ви приїжджаєте в інше визначення зазначеної мови, то як вправа, доведемо свою еквівалентність.
Мова L називається таким алгоритмом B, який на x.L алгоритм B(x) виходи 1, а на x.L виходи 0. Будь-яка важка мова має доказову систему, в якій доказ порожній. Природне питання – будь-яка мова, яка має доказову систему. Є мови, для яких є доказові системи, але для яких немає алгоритму вирішення. Не складно придумати приклад такої мови, складніше придумати природний приклад. Розглянемо мову, яка складається з поліноміалів з цілими коефіцієнтами від багатьох змінних, які йдуть до нуля принаймні для цілого значення змінних. Система доказів для такої мови проста: доказ буде ціле значення змінних, в яких поліномія є нульовою. теорема DPRM (назване після авторів: Девіс, Путнам, Робінсон і Матіяєвич) стверджує, що ця мова не є обов'язковою, тобто немає алгоритму, який перевірить, чи йде поліноміна на нулі в цілих точках. Останнім кроком у прийнятті цієї теореми відноситься до академіка Ю.В. Матясевича і ця теорема дає негативну відповідь на 10 задачу Гілберта.
Короткі докази
Поки ми не кладемо ніяких обмежень на алгоритм, який перевіряє доказ і розмір доказу. Чи буде корисно довести правильність результату програми, якщо час потрібно перевірити доказ довше виконання програми? Здається, що такі докази неспроможні, тому нам буде потрібно, щоб алгоритм A(x,w) у визначенні доказової системи працюватиме в поліномії від довжини лінії x і від довжини доказа w часу такі доказові системи будуть називатися ефективні.

Повідомляємо, що мова L належить до класу NP, якщо вона має ефективну систему доказів та поліномії, яка для будь-якого x,L є доказом належності x, Довжина L не більше, ніж p (сховища). Мова L належить до класу P, якщо існує багатомовний алгоритм часу, який перевіряє, що вхідний рядок належить до мови L. Class P міститься в класі NP, тому що для кожної мови L від P, алгоритм, який перевіряє для L, є доказовою системою, якщо вважається ігнорування доказу. На даний момент не відомо, чи є мова NP, яка не належить до класу P. Проголошено питання рівності класів П та НПП щодо переліку семи завдань тисячоліття, складених Інститутом Клей, для вирішення цієї проблеми було оголошено мільйон доларів. Багато чули про перелік завдань тисячоліття у зв'язку з доказом гіпотези Поінкаре Г. Я. Перельман. Більшість експертів вважають, що P і NP класи не такі ж.
Давайте подивимося на NP клас:
Інтерактивні докази
Поки, докази, які ми шукали, були дуже схожими на те, що ми звикли, а саме, доказ є певним текстом, який, хоча це не зрозуміло, як винахідити, легко перевірити, є алгоритм, який перевіряє дійсність доказів. Для того, щоб отримати доказ, потрібно мати деякі спеціальні здібності, і кожен може перевірити доказ. По суті, не всі докази сучасної математики мають таку властивість. По-перше, докази не написані формальною мовою, яка зручна для автоматичної перевірки, і другий, вона займає кілька років, щоб зрозуміти докази в деяких областях, щоб вивчити поле.
У математичних колах для школярів цей формат занять часто практикується: діти дають набір завдань, коли дитина вважає, що він вирішить проблему, тоді він по-справжньому розповідає про рішення вчителя. І є діалог між вчителям і студентом, який або переконує вчителя, що проблема вирішується або не переконує.
Розглянемо приклад інтерактивного доказу: існує програма, яка вирішує проблему ізоморфізму графіків. У випадку, коли графіки ізоморфні, програма може довести правильність її відповіді, видаючи перестановку, яка визначає ізоморфізм. Покажіть, як ви можете довести в діалог, що графіки неізоморфні. Нехай користувач запитує програму, якщо графіки G0 і G1 єоморфними і отримайте відповідь, що вони неізоморфні. Після цього користувач отримує монету (видає випадковий елемент і з набору {0.1}) і вибирає випадкову перестановку n-element (всі перестановки вважаються однаковими ймовірними) σ. І запитує програму, чи є графіки G0, σ (Gi). Якщо i=0, програма очікується відповісти на те, що графіки isomorphic, і якщо i=1, графіки будуть очікувані неізоморфними. Якщо графіки G0 і G1 були дійсно неізоморфними, то програма легко дасть відповідь на це питання. І якщо G0 і G1 були ізоморфними, то графік σ (Gi) може однаково ймовірно бути як перестановка G0 і перестановка G1, тому програма дасть очікувану відповідь з ймовірністю не більше 1/2. Імовірність похибки може бути зменшена, повторюючи алгоритм n разів і позбавляючи те, що алгоритм працює правильно, якщо правильною відповідь була надана в кожному з n трас; ймовірність помилки в цьому випадку не перевищує 1/2n.
У прикладі просто обговорюється, що доказ є діалогом між доводником (програмою) і виверженням (користувачем), тоді як доводитель може бути дуже складним, і вивержувач може робити тільки прості речі (для розрахунку на поліномічний час). Якщо елемент x,L, то доводитель повинен мати ймовірність 1 переконувати виверизатор, і якщо x,L, вивержувач повинен прийняти такий доказ з ймовірністю не більше 1/10. теорема Шаміра стверджує, що такі інтерактивні системи коротко діалозі існують для всіх мов L, для яких є алгоритми розпізнавання за допомогою поліномної пам'яті. Зокрема, можна довести в поліномний час, що в графі немає Гамільтонського шляху.
Zero-disclosure відгуки
Поняття доказів не тільки в галузі математики і комп'ютерної науки, але і в законі. Наприклад, якщо особа обвинувачена злочином, вони можуть довести, що вони не були на сцені злочину, але не хочуть повідомляти, де вони були насправді (наприклад, вони можуть бути на господині або хочуть приховати їх від конкурентів). Алібі не є злочином, але це дуже небажано. Виявляється, що теоретично можна довести таким чином, щоб не забезпечити зайву інформацію, крім перевіреної заяви.
Розглянемо приклад: яка фірма пише програми, які швидко вирішують проблему ізоморфізму графіків, але безкоштовна версія цієї програми просто говорить, чи є графіки ізоморфними або ні, не видаючи перестановки у випадку, коли графіки ізоморфні. Для отримання перестановки необхідно придбати платну версію програми. Але в той же час розробники хочуть, щоб користувач міг перевірити, що графіки дійсно ізоморфні, але ця інформація не допомагає користувачу знайти цей ізоморфізм самостійно. Це можна зробити наступним чином: якщо графіки G0 і G1 ізоморфні, то можна вибрати випадковий перестановку π і дати графіку G2=π (G1) і попросити користувача визначити, які графіки він хоче отримати G0 і G2 або G1 і G2. Програма буде відповідати одному з цих запитів. Якщо програма знає ізоморфізм, то вона буде легко відповісти на запит користувача, але якщо немає ізоморфізму, то принаймні один з варіантів запиту користувача не зможе дати відповідь. І якщо користувач вибирає запит випадковим чином, ймовірність того, що існує ізоморфізм між параметрами, вибраними користувачем, не перевищує 1/2. Похибка може бути зменшена, повторюючи процес, вибравши новий перестановку і підказуючи користувача, щоб вибрати новий.
Виявляється, для кожної мови в класі НП, під деякими криптографічними припущеннями, можливе створення інтерактивного доказу речей, що не дає ніякої інформації про класичну докази приналежності (що існує для будь-якої мови в класі НП). Ця криптографічна припущення є існування однієї з функцій, тобто функцій, які легко обчислюються, але складно змінити. Наприклад, багато людей вважають, що функція, яка виробляє дві цифри n-bit, є одностороннім.
Вигідні докази
Нехай вчитель математики дасть студентам домашню роботу, вони дають йому блокноти з розчином. Будь-який вчитель математики мріє про те, щоб перевірити розчин без читання його в цілому. Варіант перевірки розчину тільки відповідей поганий, так як відповідь може бути знята або здогадується, і вона також не допомагає в проблемах доказів, в яких немає відповіді як такі. З’ясуйте, що це мрія викладачів є добірним і будь-яким доказом можна перевернути таким чином, що достатньо, щоб виглядати на постійній кількості біт доказів, щоб перевірити його.
Додайте приклад для мови пар неізоморфних графів GNI. У нашому прикладі доказ буде прострочена довжина, а саме для графіків на n вершинах, доказ має розмір 2n(n-1)/2, тут n(n-1)/2 є максимальною кількістю країв, які граф може мати на вершинах n. За допомогою неізоморфної пари графіків G0 і G1 є трохи струна w довжиною 2n(n-1)/2, яка індексується усіма різними графіками при n вершинах. Укус рядка w, що відповідає графу H, є нульовим, якщо H isomorphic G0, один, якщо графік isomorphic G1, і дорівнює що, якщо граф H не єоморфним або G0 або G1. На малюнку показано приклад такого рядка w для двох неізоморфних графіків на трьох вершинах:

Тестування такого доказа є інтерактивним доказом: один повинен toss a coin (забрати випадковий i від {0.1}), випадковий перестановка σ і подивитися на біт доказів, що відповідає графу σ(Gi), якщо він збігається з i, то приймає такий доказ, якщо він не збігається з i, то відхилити. Якщо графіки G0 і G1 неізоморфні, такий доказ буде прийнятий. Якщо графіки G0 і G1 ізоморфні, то графік σ(Gi) може однаково ймовірним бути перестановка G0 і G1, тому доказ буде прийнятий з ймовірністю не більше 1/2. Після повторення цього тесту 10 разів для самостійних випадкових відборів і σ, ймовірність помилки можна зменшити до 1/1024.
Недолік вищезазначеного доказу полягає в тому, що він має обмежений розмір. Тим не менш, відомий теорема ПКП (PCP - це скорочення для пробабалістично перевірених доказів) станів, які для кожної мови в класі NP є доказом приналежності до мови поліномного розміру, і для перевірки цього доказу достатньо, щоб прочитати постійний номер біт цього доказу. Більш того, звичайний доказ (який існує за визначенням класу NP) може бути перетворений в доказ, який може бути імовірно перевірений в поліномічному часі.
теорема ПКП не тільки веселий факт, але і потужний інструмент для досягнення складності приблизних рішень для задач оптимізації. Нагадаємо, що самостійний набір в графі називається набором вершин графа, між якими немає краю графіка. Відомо, що задача пошуку максимального самостійного набору в графі NP-difficult, що означає, зокрема, що якщо існує багатомовний алгоритм від кількості вершин графіка, який знаходить найбільш самостійний набір в графі, а потім P = NP. За допомогою теореми PCP можна довести, що задача NP-difficult полягає в тому, щоб знайти не тільки оптимальний набір, але і приблизний мінімум (з постійним наближенням). Зокрема, якщо є алгоритм, який знаходить самостійний набір в графі в поліномічному часі, який не більше 1000 разів менше, ніж в максимальному обсязі, то це випливає, що P = NP.
Посилання
Література, в якій можна знайти строгі рецептури та докази всіх заяв, зазначених у статті:
Зацікавлені теоретичними інформатиками рекомендується звертати увагу на ступінь магістра університету.
Джерело: habrahabr.ru/company/spbau/blog/217215/

Для того, щоб пояснити, які докази ми будемо говорити про, будь ласка, зайдіть приклад: є комп'ютерна програма, автори якої стверджують, що програма робить щось конкретним (специфічні приклади будуть дані пізніше). Ви можете запустити програму і отримати відповідь. Як ви впевнені, що програма, яка повинна робити? Це буде добре, якщо, крім відповіді, програма забезпечить доказ того, що ця відповідь є правильним.
Розглянемо більш конкретний приклад: ми хочемо мати програму, яка знаходить максимальний розмір парі в двосторонньому графі разом з підтвердженням його максимальності.

Нагадаємо, що граф називається біпартитом, якщо його вершини можна пофарбувати в два кольори, щоб краю графіка з'єдналися вершини різних кольорів. Парад в графі називається таким набором ребер, які не мають двох з них спільного кінця. Набір вершин графа називається покриттям, якщо кожен край графіка має принаймні один кінець в цьому наборі. теорема Коеніга говорить про те, що в двосторонньому графі розмір максимальної пари збігається з розмірами мінімального комплекту покриття. Таким чином, щоб довести, що відповідність є максимальним, можна пред'явити встановлене покриття розміром якого збігається з розмірами цієї пари. Дійсно, цей набір покриття буде мінімальним, так як кожен набір покриття повинен покрити принаймні один кінець кожного краю цієї пари. Наприклад, в графі на малюнку парування (M1, G3), (M2, G2), (M4, G1) буде максимальним, так як є набір покриття розміром 3, який складається з G2, G3 і M4. Зверніть увагу, що набагато простіше перевірити такий доказ, ніж розрахувати максимальну пару: просто перевірте, що розмір парі збігається з розмірами комплекту покриття і перевірте, що всі ребра вкриті.
Розглянемо ще один приклад, давайте сказати, що нам потрібна програма, яка тестує систему необмежених лінійних нерівностей з раціональними коефіцієнтами сумісності (щодо того, що система нерівностей називається спільним, якщо ви можете знайти такі значення змінних, які всі нерівності будуть виконані).
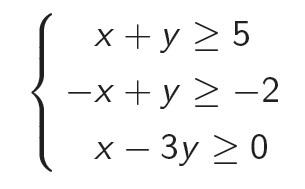
Як можна довести правильність результату? Якщо система кооперативна, то підтвердження співпраці може бути розчином системи (непросто довести, що якщо така система має рішення, то є раціональне рішення, тобто його можна писати). Як ви доведете, що система не сумісна? Виявляється, що це можна зробити за допомогою леймази Farkas, що говорить про те, що якщо система незрівнянних лінійних нерівностей несумісна, то можна додати ці нерівності з ненегативними коефіцієнтами і отримати суперечливу нерівність 0 ≥ 1. Наприклад, система на малюнку несумісна, і якщо додати перше рівняння з коефіцієнтом 1, другий з коефіцієнтом 2, а третій з коефіцієнтом 1, ви отримуєте 0 ≥ 1. Вистоювання несумісних коефіцієнтів буде просто набором негативних коефіцієнтів.
У цій статті ми будемо говорити про те, чи потрібен доказ, чи є перевірка доказів завжди не простіше, ніж рішення проблеми самостійно. (На прикладі максимального узгодження ми не доведемо, що не існує алгоритму, який вирішує проблему одночасно, оскільки це вимагає перевірки доказу.) Якщо ми не обмежуємо розмір доказу, ми знайдемо, що докази необхідно, і якщо ми вимагаємо, що докази будуть правильними, то питання необхідності доказування є еквівалентним найважливішим відкритим питанням рівності класів P і NP. Далі ми будемо говорити про інтерактивні докази. Поговоримо криптографічні докази, які не мають зайвої інформації, окрім правди перевіреної претензії. І ми завершуємо обговорення ймовірних доказів і відомої теореми ПКП, яка використовується для доведення труднощів приблизних задач оптимізації.
У цій статті ми не будемо торкнутися на автоматичний доказ теорем і доказ вірності програм, хоча ці теми також досить цікаві.
Чи потрібна допомога?
Мова - набір ліній над скінченним алфавітом. В теоретичній комп'ютерній науці зазвичай розглядаються докази виписок xaL, де L мова і x є рядком. Заяви такого роду узагальнені математичні теореми, оскільки будь-які математичні теореми, що заява, написана у формальній мові, належить до набору вірних виписок.
Система доказування мови L називається алгоритмом A(x,w), який отримує дві лінії в вході: x і w і перевіряє, що рядок w є доказом належності x,L. Два властивості необхідні для доказової системи: виправлення і повноти. Виправленість стверджує, що якщо для деяких рядків x і w алгоритм A(x,w) виходи 1, потім x,L. Повністю станів, які для кожного x,L є такий рядок, що алгоритм A(x,w) виходи 1.
Мови, для яких існують доказові системи. Якщо ви приїжджаєте в інше визначення зазначеної мови, то як вправа, доведемо свою еквівалентність.
Мова L називається таким алгоритмом B, який на x.L алгоритм B(x) виходи 1, а на x.L виходи 0. Будь-яка важка мова має доказову систему, в якій доказ порожній. Природне питання – будь-яка мова, яка має доказову систему. Є мови, для яких є доказові системи, але для яких немає алгоритму вирішення. Не складно придумати приклад такої мови, складніше придумати природний приклад. Розглянемо мову, яка складається з поліноміалів з цілими коефіцієнтами від багатьох змінних, які йдуть до нуля принаймні для цілого значення змінних. Система доказів для такої мови проста: доказ буде ціле значення змінних, в яких поліномія є нульовою. теорема DPRM (назване після авторів: Девіс, Путнам, Робінсон і Матіяєвич) стверджує, що ця мова не є обов'язковою, тобто немає алгоритму, який перевірить, чи йде поліноміна на нулі в цілих точках. Останнім кроком у прийнятті цієї теореми відноситься до академіка Ю.В. Матясевича і ця теорема дає негативну відповідь на 10 задачу Гілберта.
Короткі докази
Поки ми не кладемо ніяких обмежень на алгоритм, який перевіряє доказ і розмір доказу. Чи буде корисно довести правильність результату програми, якщо час потрібно перевірити доказ довше виконання програми? Здається, що такі докази неспроможні, тому нам буде потрібно, щоб алгоритм A(x,w) у визначенні доказової системи працюватиме в поліномії від довжини лінії x і від довжини доказа w часу такі доказові системи будуть називатися ефективні.

Повідомляємо, що мова L належить до класу NP, якщо вона має ефективну систему доказів та поліномії, яка для будь-якого x,L є доказом належності x, Довжина L не більше, ніж p (сховища). Мова L належить до класу P, якщо існує багатомовний алгоритм часу, який перевіряє, що вхідний рядок належить до мови L. Class P міститься в класі NP, тому що для кожної мови L від P, алгоритм, який перевіряє для L, є доказовою системою, якщо вважається ігнорування доказу. На даний момент не відомо, чи є мова NP, яка не належить до класу P. Проголошено питання рівності класів П та НПП щодо переліку семи завдань тисячоліття, складених Інститутом Клей, для вирішення цієї проблеми було оголошено мільйон доларів. Багато чули про перелік завдань тисячоліття у зв'язку з доказом гіпотези Поінкаре Г. Я. Перельман. Більшість експертів вважають, що P і NP класи не такі ж.
Давайте подивимося на NP клас:
- Мова з'єднання чисел в класі NP. Щоб довести, що число n є композитним, достатньо для представлення двох цілих і б, які більше, ніж єдність і n = a. Мова прем'єрних чисел також в класі NP, але набагато складніше довести її. Тим не менш, у 2002 році Каял і Саксена довели, що мова праймових (і тому з'єднання) чисел знаходиться в класі P.
- Розглянемо GI, що складається з пар ізоморфних графіків. Ми вважаємо, що вершини графіків занурюються за номерами від 1 до n, кожен
Край з'єднує рівно одну пару вершин. Два графіки G1(V1,E1) і G2(V2,E2) називаються ізоморфним, якщо вершини першого графіка можуть бути змінені таким чином, що перший графік стає таким же, як другий графік. Це означає, що після нумерації набір ребер першого графіка збігається з набором ребер другого графіка. Мова GI полягає в класі NP, підтвердження ізоморфних графіків буде перепланування вершин першого графіка, який встановлює ізоморфізм. Якщо GI є в класі P є відкритим питанням. Розглянемо також мову ГНІ, яка складається з пар неізоморфних графів на тій же кількості вершин. Не відомо, чи є GNI в NP, оскільки це не зрозуміло, як коротко довести, що два графіки неізоморфні. - Розглянемо мову HamPath, яка складається з графіків, які мають Гамільтонський шлях, тобто шлях, який проходить через кожну вершину точно один раз. Ця мова знаходиться в класі NP, оскільки сама шлях може використовуватися як доказ шляху. Не відомо, що це в класі P, але відомо, що це NP-повна. Останнє зокрема означає, що HamPath не лягає в P, якщо P,NP. Крім мови HamPath збігається з багатьма графіками, які не мають Гамільтонського шляху. Чи не існує доповнення HamPath у класі NP.
Інтерактивні докази
Поки, докази, які ми шукали, були дуже схожими на те, що ми звикли, а саме, доказ є певним текстом, який, хоча це не зрозуміло, як винахідити, легко перевірити, є алгоритм, який перевіряє дійсність доказів. Для того, щоб отримати доказ, потрібно мати деякі спеціальні здібності, і кожен може перевірити доказ. По суті, не всі докази сучасної математики мають таку властивість. По-перше, докази не написані формальною мовою, яка зручна для автоматичної перевірки, і другий, вона займає кілька років, щоб зрозуміти докази в деяких областях, щоб вивчити поле.
У математичних колах для школярів цей формат занять часто практикується: діти дають набір завдань, коли дитина вважає, що він вирішить проблему, тоді він по-справжньому розповідає про рішення вчителя. І є діалог між вчителям і студентом, який або переконує вчителя, що проблема вирішується або не переконує.
Розглянемо приклад інтерактивного доказу: існує програма, яка вирішує проблему ізоморфізму графіків. У випадку, коли графіки ізоморфні, програма може довести правильність її відповіді, видаючи перестановку, яка визначає ізоморфізм. Покажіть, як ви можете довести в діалог, що графіки неізоморфні. Нехай користувач запитує програму, якщо графіки G0 і G1 єоморфними і отримайте відповідь, що вони неізоморфні. Після цього користувач отримує монету (видає випадковий елемент і з набору {0.1}) і вибирає випадкову перестановку n-element (всі перестановки вважаються однаковими ймовірними) σ. І запитує програму, чи є графіки G0, σ (Gi). Якщо i=0, програма очікується відповісти на те, що графіки isomorphic, і якщо i=1, графіки будуть очікувані неізоморфними. Якщо графіки G0 і G1 були дійсно неізоморфними, то програма легко дасть відповідь на це питання. І якщо G0 і G1 були ізоморфними, то графік σ (Gi) може однаково ймовірно бути як перестановка G0 і перестановка G1, тому програма дасть очікувану відповідь з ймовірністю не більше 1/2. Імовірність похибки може бути зменшена, повторюючи алгоритм n разів і позбавляючи те, що алгоритм працює правильно, якщо правильною відповідь була надана в кожному з n трас; ймовірність помилки в цьому випадку не перевищує 1/2n.
У прикладі просто обговорюється, що доказ є діалогом між доводником (програмою) і виверженням (користувачем), тоді як доводитель може бути дуже складним, і вивержувач може робити тільки прості речі (для розрахунку на поліномічний час). Якщо елемент x,L, то доводитель повинен мати ймовірність 1 переконувати виверизатор, і якщо x,L, вивержувач повинен прийняти такий доказ з ймовірністю не більше 1/10. теорема Шаміра стверджує, що такі інтерактивні системи коротко діалозі існують для всіх мов L, для яких є алгоритми розпізнавання за допомогою поліномної пам'яті. Зокрема, можна довести в поліномний час, що в графі немає Гамільтонського шляху.
Zero-disclosure відгуки

Поняття доказів не тільки в галузі математики і комп'ютерної науки, але і в законі. Наприклад, якщо особа обвинувачена злочином, вони можуть довести, що вони не були на сцені злочину, але не хочуть повідомляти, де вони були насправді (наприклад, вони можуть бути на господині або хочуть приховати їх від конкурентів). Алібі не є злочином, але це дуже небажано. Виявляється, що теоретично можна довести таким чином, щоб не забезпечити зайву інформацію, крім перевіреної заяви.
Розглянемо приклад: яка фірма пише програми, які швидко вирішують проблему ізоморфізму графіків, але безкоштовна версія цієї програми просто говорить, чи є графіки ізоморфними або ні, не видаючи перестановки у випадку, коли графіки ізоморфні. Для отримання перестановки необхідно придбати платну версію програми. Але в той же час розробники хочуть, щоб користувач міг перевірити, що графіки дійсно ізоморфні, але ця інформація не допомагає користувачу знайти цей ізоморфізм самостійно. Це можна зробити наступним чином: якщо графіки G0 і G1 ізоморфні, то можна вибрати випадковий перестановку π і дати графіку G2=π (G1) і попросити користувача визначити, які графіки він хоче отримати G0 і G2 або G1 і G2. Програма буде відповідати одному з цих запитів. Якщо програма знає ізоморфізм, то вона буде легко відповісти на запит користувача, але якщо немає ізоморфізму, то принаймні один з варіантів запиту користувача не зможе дати відповідь. І якщо користувач вибирає запит випадковим чином, ймовірність того, що існує ізоморфізм між параметрами, вибраними користувачем, не перевищує 1/2. Похибка може бути зменшена, повторюючи процес, вибравши новий перестановку і підказуючи користувача, щоб вибрати новий.
Виявляється, для кожної мови в класі НП, під деякими криптографічними припущеннями, можливе створення інтерактивного доказу речей, що не дає ніякої інформації про класичну докази приналежності (що існує для будь-якої мови в класі НП). Ця криптографічна припущення є існування однієї з функцій, тобто функцій, які легко обчислюються, але складно змінити. Наприклад, багато людей вважають, що функція, яка виробляє дві цифри n-bit, є одностороннім.
Вигідні докази
Нехай вчитель математики дасть студентам домашню роботу, вони дають йому блокноти з розчином. Будь-який вчитель математики мріє про те, щоб перевірити розчин без читання його в цілому. Варіант перевірки розчину тільки відповідей поганий, так як відповідь може бути знята або здогадується, і вона також не допомагає в проблемах доказів, в яких немає відповіді як такі. З’ясуйте, що це мрія викладачів є добірним і будь-яким доказом можна перевернути таким чином, що достатньо, щоб виглядати на постійній кількості біт доказів, щоб перевірити його.
Додайте приклад для мови пар неізоморфних графів GNI. У нашому прикладі доказ буде прострочена довжина, а саме для графіків на n вершинах, доказ має розмір 2n(n-1)/2, тут n(n-1)/2 є максимальною кількістю країв, які граф може мати на вершинах n. За допомогою неізоморфної пари графіків G0 і G1 є трохи струна w довжиною 2n(n-1)/2, яка індексується усіма різними графіками при n вершинах. Укус рядка w, що відповідає графу H, є нульовим, якщо H isomorphic G0, один, якщо графік isomorphic G1, і дорівнює що, якщо граф H не єоморфним або G0 або G1. На малюнку показано приклад такого рядка w для двох неізоморфних графіків на трьох вершинах:

Тестування такого доказа є інтерактивним доказом: один повинен toss a coin (забрати випадковий i від {0.1}), випадковий перестановка σ і подивитися на біт доказів, що відповідає графу σ(Gi), якщо він збігається з i, то приймає такий доказ, якщо він не збігається з i, то відхилити. Якщо графіки G0 і G1 неізоморфні, такий доказ буде прийнятий. Якщо графіки G0 і G1 ізоморфні, то графік σ(Gi) може однаково ймовірним бути перестановка G0 і G1, тому доказ буде прийнятий з ймовірністю не більше 1/2. Після повторення цього тесту 10 разів для самостійних випадкових відборів і σ, ймовірність помилки можна зменшити до 1/1024.
Недолік вищезазначеного доказу полягає в тому, що він має обмежений розмір. Тим не менш, відомий теорема ПКП (PCP - це скорочення для пробабалістично перевірених доказів) станів, які для кожної мови в класі NP є доказом приналежності до мови поліномного розміру, і для перевірки цього доказу достатньо, щоб прочитати постійний номер біт цього доказу. Більш того, звичайний доказ (який існує за визначенням класу NP) може бути перетворений в доказ, який може бути імовірно перевірений в поліномічному часі.
теорема ПКП не тільки веселий факт, але і потужний інструмент для досягнення складності приблизних рішень для задач оптимізації. Нагадаємо, що самостійний набір в графі називається набором вершин графа, між якими немає краю графіка. Відомо, що задача пошуку максимального самостійного набору в графі NP-difficult, що означає, зокрема, що якщо існує багатомовний алгоритм від кількості вершин графіка, який знаходить найбільш самостійний набір в графі, а потім P = NP. За допомогою теореми PCP можна довести, що задача NP-difficult полягає в тому, щоб знайти не тільки оптимальний набір, але і приблизний мінімум (з постійним наближенням). Зокрема, якщо є алгоритм, який знаходить самостійний набір в графі в поліномічному часі, який не більше 1000 разів менше, ніж в максимальному обсязі, то це випливає, що P = NP.
Посилання
Література, в якій можна знайти строгі рецептури та докази всіх заяв, зазначених у статті:
- Арора С. Б. Барак, порівняльна складність: сучасний підхід
- О. Goldreich, Фонди Cryptogtaphy
- Я.В. Матясевич, Десятий проблем Гільберта. — М: Наука, 1993. ISBN — 502014326X
- Верещегін Н.К., Теоретичні проблеми криптографії, конектні лекції
- Д.М. Йогоксон, Огляд курсу теоретичної інформатики, лекція резюме
Зацікавлені теоретичними інформатиками рекомендується звертати увагу на ступінь магістра університету.
Джерело: habrahabr.ru/company/spbau/blog/217215/