Переглянути невидимість

Кілька років тому в Habre було два статті, які згадували цікавий алгоритм. У статті, однак, були написані неправильно. У стилі «новини» (1, 2), але посилання на сайт було презентовано, можна детально розібратися на місці (алгоритм для авторства МІТ). І був чарівний. Невидимий алгоритм. Як автори на Habre не помітили це і зосередилися на тому, що алгоритм дозволив бачити імпульс. Пропуск точки.

Алгоритм допускаються посилені рухи, які були невидимими до очей, щоб показати речі, які ніхто не бачив живого. Відео вище - презентація другої частини алгоритму cfqnf MIT. Microsaccades, які даються з 29-ї секунди, раніше спостерігали тільки як відображення дзеркал, встановлених на учнів. Ви можете бачити їх очима.
Кілька тижнів тому я знову прийшов на ці статті. Я був негайно цікавим: що люди зробили в ці два роки готові? Але... Непристойність. Що встановити задоволення на наступний тиждень і половину. Хочу зробити той самий алгоритм і зрозуміти, що можна зробити з ним і чому він все ще не в кожному смартфоні, хоча б виміряти пульс.
У статті буде багато matan, відео, фотографії, трохи коду і відповіді на питання.

Почнемо з математикою (Я не збираюся дотримуватися однієї конкретної статті, але я збираюсь отримати шлях різних частин різних статей для більш гладкої оповіді). Команда дослідників має два основні роботи по алгоритмічної частини:
1) Емлерійський відео Magnification for Revealing Subtle Зміни у світі
(2) Обробка відеообміну
У першій роботі реалізується амплітудний підхід, більш грубий і швидше. Це те, що я використовував як основу. У другій роботі, крім амплітуди використовується фаза сигналу. Це дозволяє отримати набагато більш реалістичний і чіткий образ. Відео, наданий до цієї роботи. Мінус є більш складним алгоритмом і обробкою, знаючи, що вилітають з реального часу без використання відеокарти.

Як ми? Що таке збільшений рух? Ампліфікація руху полягає в тому, коли ми прогнозуємо, що спосіб сигналу буде перемішати і перемістити його далі.

У нас є одновимірний ресивер. На цьому приймачі ми бачимо сигнал I(x,t)=f(x). Картина намальована в чорному кольорі (на даний момент т). На наступний момент часу сигнал I(x,t+1) = f(x+Δ) (синій). Для посилення цього сигналу необхідно отримати сигнал I'(x,t+1)= f(x+(1+α)Δ. Тут α є набутком. Поставляючи його в серії Taylor, він може бути виражений як:
Скажіть:
Що таке B? Жорстко кажучи, I(x,t+1)-I(x,t). Малюнок:

Звичайно, це не точна, але як груба апроксимація буде робити (синій графік показує форму такого «закритого» сигналу). Якщо ми розмножуємо B по (1+α), це буде посилення сигналу. Ось ми йдемо (червоний графік):

У реальних пострілах може бути кілька рухів, кожен з яких буде йти на різну швидкість. Наведений метод є лінійним прогнозом, без ревізії він зламається. Але є класичний підхід до вирішення цієї проблеми, яка була використана в роботі - розпоряджувати руху відповідно до частотних характеристик (як просторовий і часовий).

На першому етапі зображення розкладається просторими частотами. Цей крок також реалізує диференціал .f(x)/.x. Перша стаття не розповідає про те, як вона працює. У другому папері при використанні фазового підходу, амплітуда і фази були розглянуті гранульовані фільтри різного порядку:

Що я зробив, коли я взяв фільтр.
І нормалізуючи його значення,
Тут л знаходиться відстань пікселя від центру фільтра. Звичайно, я обдурив трохи, взявши такий фільтр тільки одне значення вікна σ. Це значно прискорило розрахунки. Виявляється трохи дивиться картина, але я вирішив не прагнути до високої точності.
Повернутися до формул. Додайте сигнал, який дає характерну відповідь при частоті ω в нашій послідовності часових кадрів. Ми вже обрали характерний просторовий фільтр з вікном σ. Це дає нам приблизний диференціал в кожній точці. Як зрозуміло з формул, залишається тільки тимчасова функція, яка дає відповідь на наш коефіцієнт руху і отримання. На відміну від синуса частоти, яку ми хочемо збільшити (це буде функція, яка дає тимчасову відповідь). Ось ми йдемо.
Звичайно, набагато простіше, ніж в оригінальній статті, але трохи менше проблем зі швидкістю.

Код і результат. Джерела для першої статті доступні на Matlab: Чому забороти колесо і написати його самостійно? Але були ряд причин, в основному пов'язаних з Matlab:

1. Якщо ви думаєте про те, що зробити щось чутливим і застосовним, код Matlab набагато важче використовувати, ніж C# + OpenCV, який перевозиться на c++ в пару годин.
2. Оригінальний код, орієнтований на роботу з збереженими відео, які мають постійний бітрейт. Для роботи з камерами, підключеними до комп'ютера з змінним бітрейтом, потрібно змінити логіку.
3. Оригінальний код реалізував найпростіші алгоритми, без будь-яких бункерів. Впровадження дещо складної версії з бункерами вже половина роботи. Крім того, незважаючи на те, що алгоритм був оригінальним, параметри його введення були не такими ж, як в статті.
4. Початковий код періодично спричинив комп'ютер для замерзання (навіть без синього екрана). Може бути просто мене, але це незручно.
5. Початковий код мав лише режим консолі. Зробляючи все візуально в Matlab, що я знаю набагато гірше, ніж VS, займе набагато довше, ніж перезаписувати все.

Я опублікував джерело на github.com і прокоментував докладно. Програма здійснює захоплення відео з камери та її аналіз в режимі реального часу. Оптимізація виявилася трохи з запасом, але можна досягти висить, розширюючи параметри. Що обрізається в назві оптимізації:

1. Використання каркаса з зменшеним розміром. Прискорює багато речей. Форма не відображала контроль розміру кадру, але якщо ви відкриєте код, рядок: "_capture.QueryFrame(). Перетворення ().PyrDown().PyrDown();"
2. Використовуйте лише один просторовий фільтр. Для ситуації, де відомий необхідний рух, втрати некритичні. Контроль параметра фільтра з форми (довжина хвилі фільтра gabor).
3. Використовуйте лише одну частоту, яка підкреслює часовий ряд. Звичайно, можна було зробити конволюцію з попередньо встановленим вікном з спектром практично без втрати продуктивності, але цей метод також добре працює. Форма контролюється як за допомогою слайдера, так і шляхом введення граничних значень.

Трохи зауважити. Всі результати були отримані на регулярній веб-камері будинку. При використанні камери з хорошими параметрами + штатив + правильне освітлення + придушення перешкод 50 Гц, якість значно поліпшить. Моя мета не була гарною картиною або покращеним алгоритмом. Мета полягає в досягненні результатів в домашніх умовах. Ну, як бонус, я хотів би записувати мій пульс, коли я граю Starctaft 2. Цікаво, скільки кіберспорту є спортом.
В результаті виходить логіка роботи:
Це просто мес. Наприклад, підведення підвалу з каркасом здійснюється в цілому:
для (int x = 0; x < Ic[ccp].I.Width; x++) для (int y = 0; y < Ic[ccp].I.Height; y++) { FF2.Data[y, x, 0] = Альфа * FF2.Data[y, x, 0]/counter; ImToDisp.Data[y, x, 0] = (byte)Math.Max(0, Math.Min(FF2.Data[y, x, 0] + ImToDisp(Y), я не знаю оптимального способу Open, 25/Data(V
Десь 90% коду не є ядром, я набираю його тіло. Але виконання нуклеуса дає хороший результат. Ви можете побачити, як скринька закриває на пару десятків сантиметрів при диханні, ви можете побачити, як опухає вени, як головка шків у збитку імпульсу.




Ось докладне пояснення того, чому головний удар від імпульсу. Насправді це повернення ін'єкції крові серця:


Звичайно, MIT любить красиві результати. Тому вони намагаються зробити їх максимально красивими. У результаті глядач отримує враження, що ця специфіка є цілою. На жаль, Набряклість вени можна побачити тільки з належним чином розміщеним підсвічуванням (тіні слід намалювати малюнок шкіри). Зміна складнощів - тільки на хорошій камері без автоконструкцій, з правим світлом і особою, яка має явні труднощі з серцем (у відео він важкий і передчасний малюк). Наприклад, в прикладі Negro, який має гарне серце, ви не бачите флуктуацію в яскравості шкіри, але збільшення зміни в тіні через мікросхему (тіні лежить акуратно з вершини донизу).

Якісні характеристики, але все ще. Відео чітко показує дихання і пульс. Давайте спробуємо їх отримати. Найлегша річ, яка приходить до розуму, є підсумком різниці між сусідніми кадрами. З тих пір, коли дихання, ця характеристика повинна бути помітна.
Отриманий графік курсуватиме через трансформацію Фур'єра, підрахунок спектру (на графіку, статистика подається близько 5 хвилин, підсумуючи спектр, розрахований на 16-секундні сегменти).


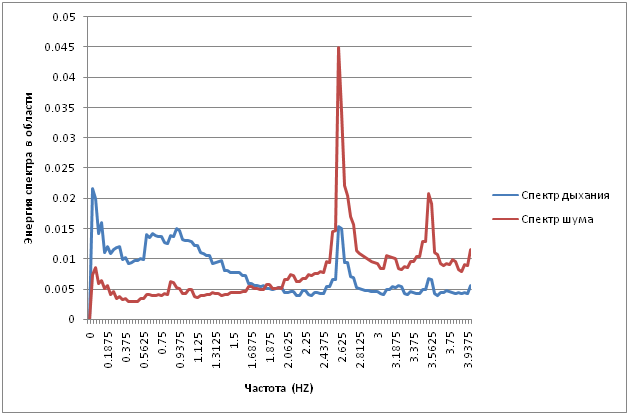
На частотах 0,6-1.3 не характерна для шуму. Оскільки дихання не є синусоїдним процесом, але процес, який має два явні лопці (інгаляційно-виключення), частота різниці малюнка повинна бути дорівнює подвійній частоті дихання. Мій рівень дихання був близько 10 дихання в 30 секунд (0.3 HZ). До 0,6ХЗ Що приблизно дорівнює виявленій максимальній спектрограмі. Але, звичайно, не потрібно говорити про точний зміст. На додаток до дихання багато тонкої моторності тіла витягується, що істотно зіпсує картину.
Є цікава вершина на 2.625HZ. Звісно, вона розбиває кінчик сітки на матрицю. Смуги скеля вздовж матриці, які успішно дають максимум при цій частоті.
До речі, подвійна частота імпульсу повинна лежати приблизно в одному діапазоні, тому цей метод не повинен працювати на ньому. І дійсно:


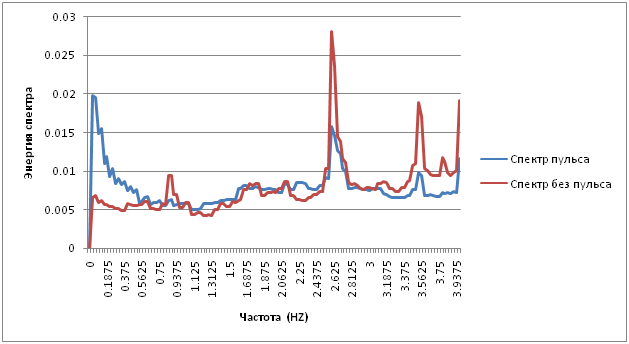
Ви не можете знайти імпульс в цьому спектрі.
В одному з робіт МІТ наведено ще один метод вимірювання швидкості імпульсу: розрахунок оптичного потоку на обличчі і визначення його частотою цього потоку. Так я зробив (спективи також на графіку):




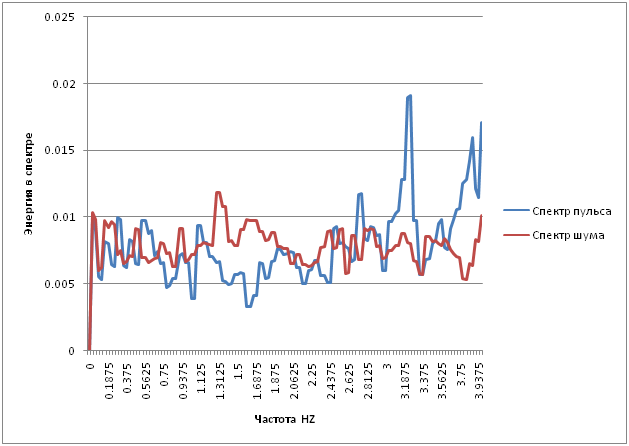
Ви можете побачити краще в графі, на якому я відключив кількість спектра maxima:


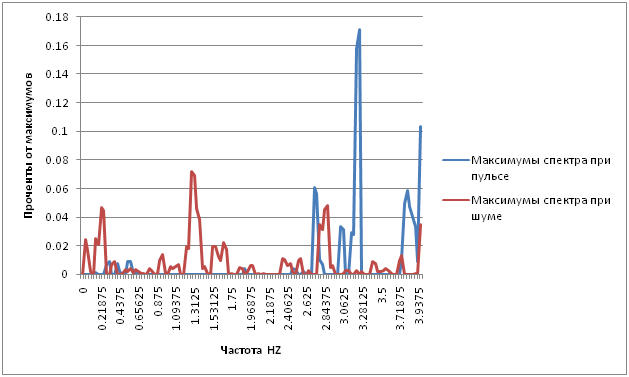
Чому максимальний при швидкості імпульсу *3 Я не знаю, як пояснити, але це максимальне, безумовно, є і прив'язується до імпульсу:
Я хотів би відзначити тільки, що отримати імпульс таким чином, ви повинні сидіти прямо і не рухатися. Коли грає Starcraft, це неможливо, частота не знімається. Ег ... Це ідея! Я повинен отримати пульсовий метр, оскільки це цікаво зараз!

В результаті я утворив свою думку про межі алгоритму, і це стало ясно мені, що його обмеження є:
Чому він не став популярним для вимірювання пульсу? Якість для веб-камер комп'ютера достатньо на кордоні, або навіть не достатньо. Android чітко не вистачає продуктивності. Спеціальні інструменти для професійного вимірювання залишаються. Але вони будуть дуже дорогими і не стійкими до зовнішніх умов (світло, мерехтливий світло, темрява, шейкінг), а якість буде нижче, ніж це перевірених засобів зйомки імпульсу.
Чому алгоритм не використовується для оцінки коливань будинків, міст, кранів? І знову. Спеціальні засоби дешевше і дають більш високу точність.
Де можна використовувати і його можна використовувати на всіх? Я думаю, що ви можете. Якщо вам потрібна видимість. Наукові відеозйомка, навчальні програми. Навчання психіатристів, психологів, пікапів працівників (найменші рухи людини помітні, посилені вирази обличчя). Проаналізувати переговори. Звичайно, потрібно використовувати не простий варіант алгоритму, але версія, яка у них є останні роботи і базується на фазовому підході. У той же час, в режимі реального часу, буде важко побачити все це, продуктивність буде недостатньо, крім того, на відео все буде паралізовано. Але можна подивитися після того, як.

Коли ви читаєте твори комрадів і перегляд відео, підозрі креветки. Я бачив все це десь. Ви дивитесь і ви думаєте, що ви думаєте. А потім вони показують відео того ж алгоритму, що й стабілізувати рух місяця, знімаючи шум атмосфери. А потім як спалах: «Так, це алгоритм пригнічення шуму, тільки з позитивним зворотним зв'язком!» І замість пригнічення паразитичних рухів вона посилює їх. Якщо ви берете α<1, то з'єднання негативно знову і рухи йдуть.
Звісно, пригнічення руху і алгоритми погойдування трохи відрізняються математикою і дещо різним підходом. Але насправді саме той самий спектральний аналіз космічних труб.
Хоча говорити про те, що алгоритм висить тут. У MIT фактично помітили одну маленьку цікаву функцію, розвивали її, і отримали всю теорію з цими красивими і чарівними фотографіями.

І, нарешті, програміст, будьте обережні! Запатентовано алгоритм, суддівство нот на сайті, Запрошення до освітнього процесу. Не існує патентування алгоритмів в Росії. Але будьте обережні, якщо ви робите щось на його основі. За межами Росії це може стати незаконним.

SubvalaSite про дослідження MIT щодо збільшення руху
Мої джерела.

З.Ю. І покажіть мені пульсовий лічильник, який може знизити дані на комп'ютері і, бажано, мати будь-який інтерфейс Android?

Джерело: habrahabr.ru/post/232515/