Увидеть незримое

Пару лет назад на Хабре проскакивало две статьи, в которых упоминался интересный алгоритм. Статьи, правда, были написаны нечитабильно. В стилистике «новости»(1, 2), но ссылка на сайт присутствовала, подробно можно было разобраться на месте (алгоритм за авторством MIT). А там была магия. Абсолютно волшебный алгоритм, позволяющий увидеть незримое. Оба автора на Хабре этого не заметили и сфокусировались на том, что алгоритм позволял увидеть пульс. Пропустив самое главное.

Алгоритм позволял усиливать движения, невидные глазу, показать вещи, которые никто никогда не видел живьём. Видео чуть выше – презентация c cfqnf MIT второй части алгоритма. Микросаккады, которые приведены начиная с 29ой секунды, раньше наблюдались только как отражения установленных на зрачках зеркалах. А тут они видны глазами.
Пару недель назад я опять натолкнулся на те статьи. Мне сразу стало любопытно: а что народ сделал за эти два года готового? Но… Пустота. Это определило развлечение на следующие полторы недели. Хочу сделать такой же алгоритм и разобраться, что с ним можно сделать и почему его до сих пор нет в каждом смартфоне, как минимум для измерения пульса.
В статье будет много матана, видео, картинок, немного кода и ответы на поставленные вопросы.

Начнём с математики (я не буду придерживаться какой-то одной определённой статьи, а буду мешать из разных частей разных статей, для более гладкого повествования). У исследовательской группы есть две основных работы по алгоритмической части:
1) Eulerian Video Magnification for Revealing Subtle Changes in the World
2) Phase-Based Video Motion Processing
В первой работе реализуется амплитудный подход, более грубый и быстрый. Его я и брал за основу. Во второй работе кроме амплитуды используется фаза сигнала. Это позволяет получить значительно более реалистичное и чёткое изображение. Видео выше прилагалось именно к этой работе. Минус – более сложный алгоритм и обработка, заведомо вылетающая из реального времени без применения видеокарты.

Начнём?

Что такое усиление движения? Усиление движения, это когда мы предсказываем в какую сторону сигнал смешается и сдвигаем его в эту сторону дальше.

Пусть у нас есть одномерный приёмник. На этом приёмнике мы видим сигнал I(x,t)=f(x). На картинке от нарисован чёрным (для некоторого момента t).В следующий момент времени сигнал I(x,t+1)= f(x+Δ) (синий). Усилить этот сигнал, это значит получить сигнал I’(x,t+1)= f(x+(1+α)Δ). Тут α – коэффициент усиления. Разложив его в ряд Тейлора его можно выразить как:
Пусть:
Что такое B? Грубо говоря это I(x,t+1)- I(x,t). Нарисуем:

Конечно, это неточно, но в качестве грубого приближения сойдёт (голубой график показыает форму такого «приближенонго» сигнала). Если мы домножим B на (1+α) это и будет «усиление» сигнала. Получаем (красный график):

В реальных кадрах может присутствовать несколько движений, каждое из которых будет идти с разной скоростью. Приведённый выше способ — линейный прогноз, без доработки он обломится. Но, есть классический подход для решения этой проблемы, который и использовался в работе — разложить движения по частотным характеристикам (как пространственным, так и временным).

На первом этапе происходит разложение изображения по пространственным частотам. Этот этап, кроме того, реализует получение дифференциала ∂f(x)/ ∂x. В первой работе не рассказано, как они его реализуют. Во второй работе, при использовании фазового подхода, амплитуда и фаза считалась фильтрами Габбора разного порядка:

Примерно так я и поступил, взяв фильтр:
И нормировав его значение, чтобы
Тут l — расстояния пикселя от центра фильтра. Конечно, я немного схалтурил, взяв такой фильтр только для одного значения окна σ. Это позволило значительно ускорить вычисления. При этом получается чуть более размазанная картинка, но я решил не стремиться за высокой точностью.
Вернёмся к формулам. Пусть мы хотим усилить сигнал, дающий характерный отклик на частоте ω в нашей временной последовательности кадров. Мы уже подобрали характерный пространственный фильтр с окном σ. Это даёт нам примерный дифференциал в каждой точке. Как понятно из формул — остаётся только временная функция, дающая отклик на наше движение и коэффициент усиления. Умножаем на синус той частоты, которую хотим усилить (это и будет функция, дающая временной отклик). Получаем:
Конечно, куда проще, чем в оригинальной статье, зато чуть-чуть меньше проблем со скоростью.

Код и результат.

Исходники к первой статье выложены в открытом доступе на Матлабе:. Казалось бы, зачем изобретать велосипед и писать самому? Но был целый ряд причин, во многом завязанных на Матлаб:

1. Если потом придёт в голову сделать что-то разумное и применимое, код на Матлабе куда сложнее использовать, чем C#+OpenCV, портирующийся за пару часов в с++.
2. Оригинальный код ориентировался на работу с сохранёнными видео, имеющее постоянный битрейт. Чтобы можно было работать с камерами, подключёнными к компьютеру, обладающими переменным битрейтом нужно менять логику.
3. Оригинальный код реализовывал самый простой из их алгоритмов, без всяких плюшек. Реализовать чуть более сложную версию с плюшками – уже пол работы. К тому же, не смотря на то, что алгоритм был оригинальным, параметры на его вводе были не те, что в статьях.
4. Оригинальный код периодически приводил к мёртвому зависанию компа (даже без синего экрана). Может только у меня, но ведь некомфортно.
5. В оригинальном коде был только консольный режим. Делать всё визуальным в Матлабе, который я знаю значительно хуже VS, было бы значительно дольше, чем всё переписать.

Исходники я выложил на github.com и достаточно подробно прокомментировал. Программа реализует захват видео с камеры и его анализ в реальном времени. Оптимизации получилось немного с запасом, но можно добиться подвисаний, расширяя параметры. Что обрезано во имя оптимизации:

1. Использование кадра с уменьшенным размером. Значительно ускоряет работу. На форму не стал выводить управление размером кадра, но если откроете код, то строчка: "_capture.QueryFrame().Convert<Bgr, float>().PyrDown().PyrDown();" это оно
2. Использование только одного пространственного фильтра. Для ситуации, когда известно желаемое движение потери некритичны. Управление параметром фильтра с формы (длинна волны фильтра Габора).
3. Использование только одной частоты, подчёркивающей временной ряд. Конечно, можно было делать свёртку с заранее рассчитанным окном со спектром почти без потери производительности, но этот способ тоже неплохо работает. С формы управляется либо ползунком, либо вводом предельных значений.

Маленькая ремарка. Все результаты получены на обычной веб-камере в домашних условиях. При использовании камеры с хорошими параметрами + штатива + правильного освещения + подавления 50ГЦ помехи качество значительно улучшится. Моей целью не было получение красивой картинки или улучшенного алгоритма. Цель – добиться результата в домашних условиях. Ну, как бонус, хотелось бы ещё сделать запись пульса когда я играю в Starctaft 2… Любопытно же, насколько e-sport таки спорт.
В итоге логика работы получается:
Всё просто до безобразия. Например суммирование прирощения с кадром реализовано вообще так:

<code>for (int x = 0; x < Ic[ccp].I.Width; x++)   for (int y = 0; y < Ic[ccp].I.Height; y++)   {       FF2.Data[y, x, 0] = Alpha * FF2.Data[y, x, 0] / counter;       ImToDisp.Data[y, x, 0] = (byte)Math.Max(0, Math.Min((FF2.Data[y, x, 0] + ImToDisp.Data[y, x, 0]), 255));    } </code>

(Да, я знаю, что при наличии OpenCV это не оптимальный способ)
Где-то 90% кода это не ядро, я обвес вокруг него. Но реализация ядра даёт уже неплохой результат. Видно как раздувается грудная клетка на пару десятков сантиметров при дыхании, видно как набухает вена, как качается голова в такт пульса.




Вот тут подробно объясняется, почему качается голова от пульса. По сути это отдача от вброса крови сердцем:

Немножко про красоту

Конечно, в MIT любят красивые результаты. И, поэтому, стараются сделать их как можно красивее. В результате у смотрящего создаётся впечатление, что эта частность это и есть целое. К сожалению нет. Разбухающую вену можно увидеть только при правильно поставленном освещении (тень должна рисовать узор кожи). Изменение цвета лица — только на хорошей камере без автокоррекции, с правильно поставленным светом и человеком, у которого имеются явные сложности с сердцем (в видео это грузный мужчина и недоношенный ребёнок). Например в примере с негром, у которого с сердцем всё хорошо, вы видите не колебание яркости кожи, а усиление изменения тени из-за микродвижений (тень аккуратно лежит сверху вниз).

Количественных характеристики

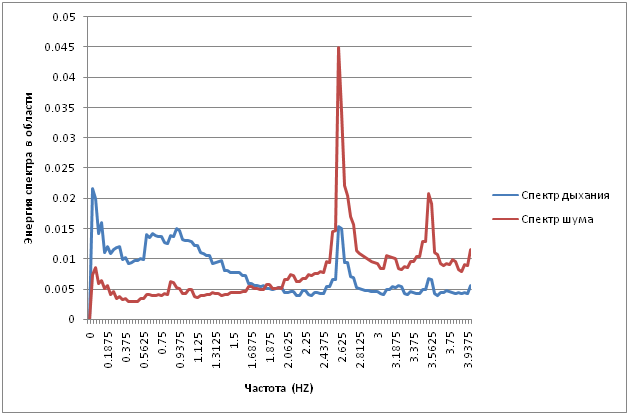
Но всё же. В видео явно видны дыхание и пульс. Давайте попробуем их получить. Самое простое, что приходит в голову — просуммированная разница между соседними кадрами. Так как при дыхании колеблется почти всё тело — эта характеристика должна быть заметна.
Полученный график прогоним через Фурье-преобразование, посчитав спектр (на графике набрана статистика где-то за 5 минут суммированием спектра, рассчитанного по 16-секундным отрезкам).


Виден явный пик на частотах 0.6-1.3, не свойственный шуму. Так как дыхание не синусоидальный процесс, а процесс, имеющий два явных всплеска (при вдохе-выдохе), то частота разностной картинки должна равняться двойной частоте дыхания. Частота дыхания у меня была где-то 10 вдохов за 30 секунд (0.3 HZ). Её удвоение — 0.6HZ. Что приблизительно равно выявленному максимуму спектрограммы. Но, понятно, о точном значении говорить не приходится. Кроме дыхания вытягивается множество мелкой моторики тела, которая значительно портит картину.
Имеется интересный пик на 2.625HZ. Судя по всему это пробивается наводка электросети на матрицу. По матрице ползут полосы, которые успешно дают максимум на этой частоте.
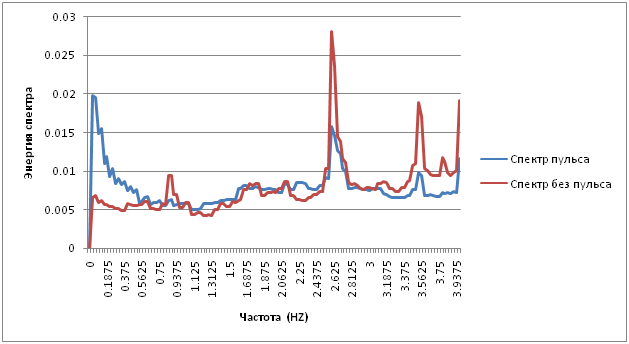
Между прочим, двойная частота пульса должна лежать примерно в том же диапазоне, а значит этот метод не должен на ней сработать. И действительно:


В таком спектре найти пульс нельзя.
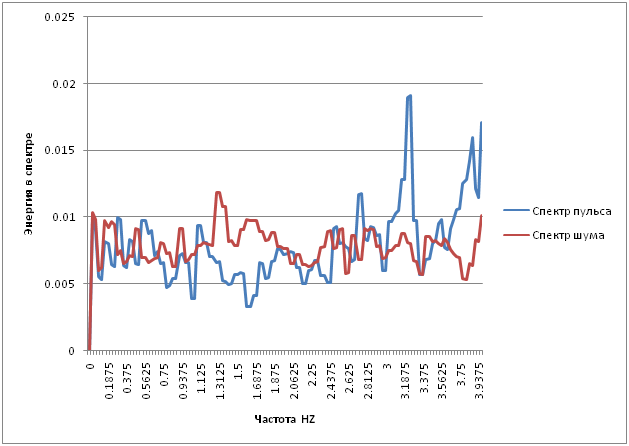
В одной из работ MIT приведён другой способ для измерения частоты пульса: вычислять оптический поток на лице и определять его по частоте этого потока. Так я и сделал (на графике тоже спектры):




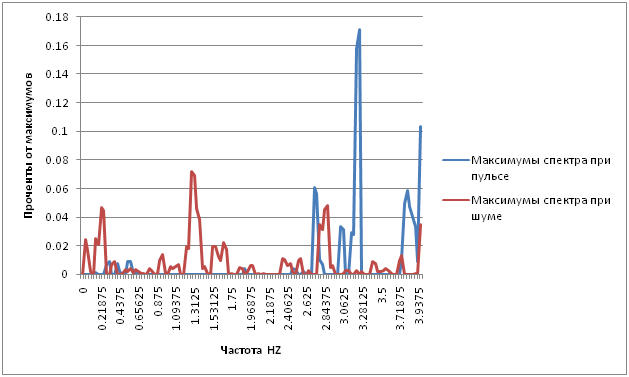
Лучше видно на графике на котором я откладывал количество максимумов спектра:


Почему максимум на частоте пульса *3 я не знаю как объяснить, но этот максимум точно есть и завязан на пульс:)
Хотелось бы отметить только, что для получения пульса таким способом нужно сидеть прямо и не двигаться. При игре в Старкрафт это невозможно, частота не снимается. Эх… А такая задумка! Придётся добывать пульсометр, ведь интересно теперь стало!

Итак, результат

В результате я достаточно чётко сформировал своё мнение о границах алгоритма, мне стало понятно, какие у него ограничения:
Почему он не стал популярным для измерения пульса? Качества для Web-камер компьютера хватает на границе, а то и не хватает. У android явно не хватит производительности. Остаются спецсредства для профессионального измерения. Но они будут очень дорогими и не стабильными к внешним условиям (засветка, мерцающий свет, темнота, тряска), а качество будет ниже, чем у проверенных средств съёмки пульса.
Почему алгоритм не используется для оценки колебаний домов, мостов, кранов? Опять же. Спецсредства дешевле и дают большую точность.
А где же его можно использовать и можно ли вообще? Думаю, что можно. Везде где нужна наглядность. Научные видеосъёмки, образовательные программы. Тренинг психиаторов, психологов, пикаперов (видны мельчайшие движения человека, усиливается мимика). Для анализа переговоров. Конечно, при этом использовать нужно не простую версию алгоритма, а ту версию, которая у них в последней работе и основана на фазовом подходе. При этом в реальном времени всё это сложно будет увидеть, производительности не будет хватать, разве что на видюхе всё распаралелить. Зато можно посмотреть постфактум.

Ничего не ново под луной

Когда читаешь работы товарищей и смотришь видео закрадывается подозрение. Где-то я всё это видел. Вот смотришь и думаешь, думаешь. А потом они показывают видео того, как с помощью этого же алгоритма берут и стабилизируют движение Луны, убирая шумы атмосферы. И тут как вспышка: «Да это же алгоритм подавления шумов, только с положительной обратной связью!!». И вместо того, чтобы подавлять паразитные движения, он их усиливает. Если взять α<1, тогда связь опять отрицательная и движения уходят!
Конечно, в алгоритмах подавления движения и тряски чуть другая математика и чуть другой подход. Но ведь по сути ровно тот же спектральный анализ пространственно-временной трубки.
Хотя говорить, что тут свиснули алгоритм глупо. В MIT реально заметили одну маленькую интересную особенность, развили её и получили целую теорию с такими красивыми и магическими картинками.

И напоследок: программист, будь аккуратен!

Алгоритм, судя по пометкам на сайте, патентуется. Использование разрешено в образовательных целях. Конечно, в России не существует патентования алгоритмов. Но будьте аккуратны, если сделаете что-то на его базе. Вне пределов России это может стать нелегально.

Подвал

Сайт про исследования MIT на тему усиления движения
Мои исходники

З.Ю. А подскажите пульсометр, который бы мог данные на комп скидывать и, желательно, какой-нить интерфейс под Android имел?

Источник: habrahabr.ru/post/232515/