562
The task that only thoughtful people can decide
< Website offers you apart from all the cases and try to solve the puzzle of logic. The solution is very simple, you only need to look closely at the picture.
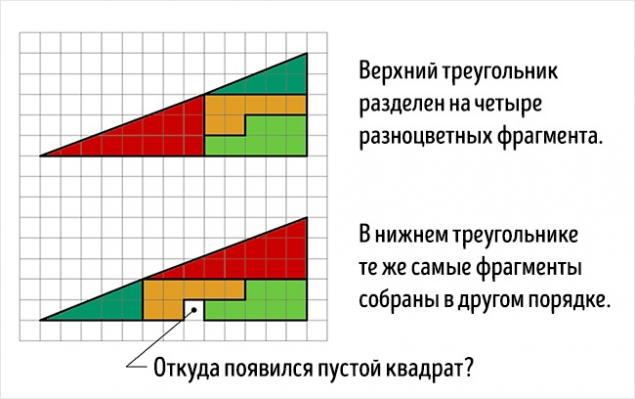
Before you two triangles. Top evenly divided into 4 fragments, painted in different colors. The lower triangle of the same sections are arranged in a different order. Attention to the question:? < where did the extra blank box
Learn the correct answer
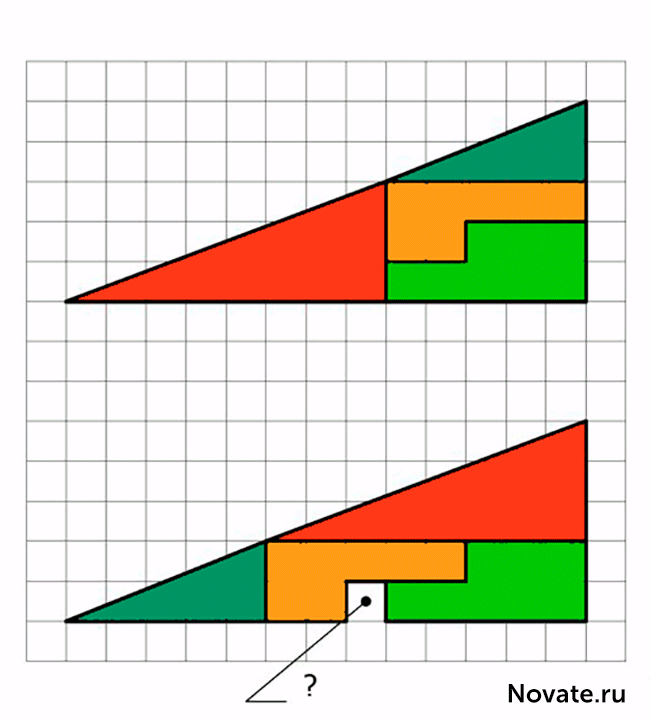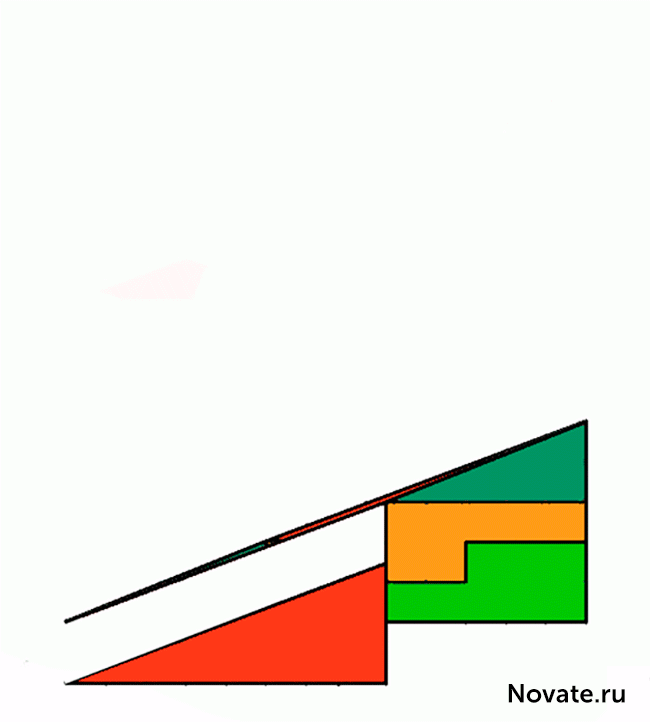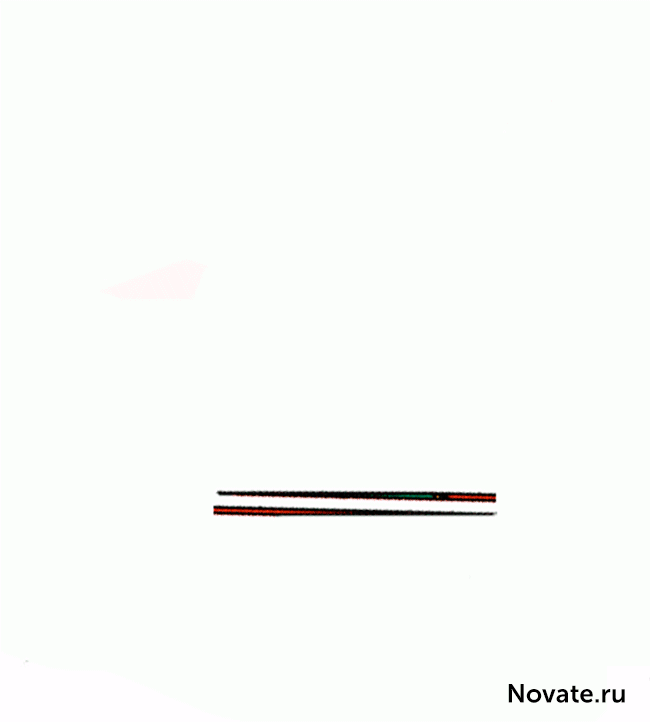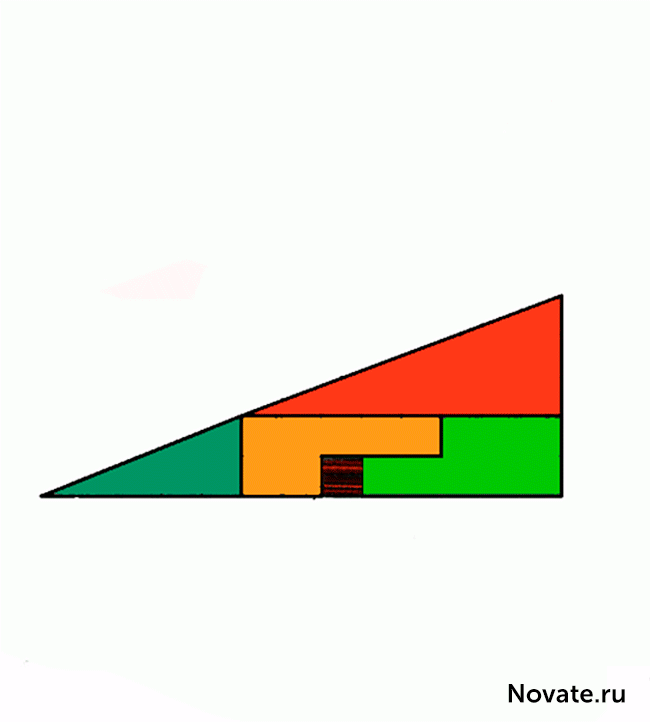
In reality, this is not an optical illusion, but interesting task. of course, the areas shaded figures are equal (32 cells), but that is observed visually as triangles × 13 5 in fact is not even as such has different areas (S 13 = 5 × 32 5 cells). That is a mistake, disguised in the problem, is that the initial figure called a triangle (in fact it is a concave quadrilateral). This is clearly noticeable in figure diagram below, where the "hypotenuse" of the upper and lower pieces pass through different points: at the top (8, 3) and the bottom (5, 2). The secret - in the properties of the blue and red triangles. It's easy to check the calculations.
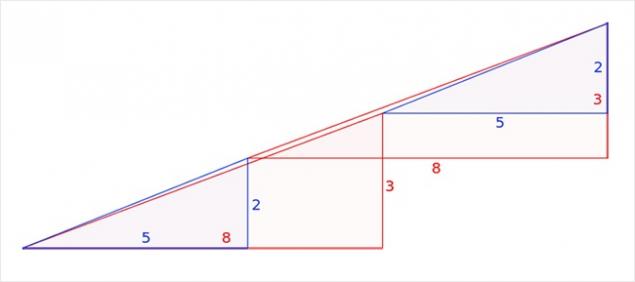
Relationship of the parties concerned lengths of blue and red triangles are not equal (2/3 and 5/8), so the triangles are not similar and, therefore, have different angles at the respective vertices. We say that the first figure is a concave quadrilateral, and the second figure is concave octagon, psevdotreugolnikami. If the lower part of these psevdotreugolnikov parallel, then the hypotenuse in both psevdotreugolnikah 13 × 5 are actually broken lines (the upper figure creates a break inside, and at the bottom - out). If we impose the top and bottom pieces 13 × 5 to each other, between their "hypotenuses" parallelogram formed, and which is contained in the "extra" area. Figure chart this parallelogram is given in correct proportions.
The acute angle of the parallelogram is 46 arcctg ≈ 0 ° 1'18, 2 ". At this angle the minute hand on the healthy-hour shifts for 12, 45 seconds. It is at such an obtuse angle value in this parallelogram is different from expanded. Visually such a tiny difference unnoticed, but it is easily visible in the animation.
According to Martin Gardner, this task has invented amateur magician from New York, Paul Curry in 1953. However, the principle laid down in it, was known in the 1860s. You can see that the sides of the figures given task length (2, 3, 5, 8, 13) are successive Fibonacci numbers.
via www.novate.ru/blogs/110316/35420/

Before you two triangles. Top evenly divided into 4 fragments, painted in different colors. The lower triangle of the same sections are arranged in a different order. Attention to the question:? < where did the extra blank box
Learn the correct answer

In reality, this is not an optical illusion, but interesting task. of course, the areas shaded figures are equal (32 cells), but that is observed visually as triangles × 13 5 in fact is not even as such has different areas (S 13 = 5 × 32 5 cells). That is a mistake, disguised in the problem, is that the initial figure called a triangle (in fact it is a concave quadrilateral). This is clearly noticeable in figure diagram below, where the "hypotenuse" of the upper and lower pieces pass through different points: at the top (8, 3) and the bottom (5, 2). The secret - in the properties of the blue and red triangles. It's easy to check the calculations.

Relationship of the parties concerned lengths of blue and red triangles are not equal (2/3 and 5/8), so the triangles are not similar and, therefore, have different angles at the respective vertices. We say that the first figure is a concave quadrilateral, and the second figure is concave octagon, psevdotreugolnikami. If the lower part of these psevdotreugolnikov parallel, then the hypotenuse in both psevdotreugolnikah 13 × 5 are actually broken lines (the upper figure creates a break inside, and at the bottom - out). If we impose the top and bottom pieces 13 × 5 to each other, between their "hypotenuses" parallelogram formed, and which is contained in the "extra" area. Figure chart this parallelogram is given in correct proportions.
The acute angle of the parallelogram is 46 arcctg ≈ 0 ° 1'18, 2 ". At this angle the minute hand on the healthy-hour shifts for 12, 45 seconds. It is at such an obtuse angle value in this parallelogram is different from expanded. Visually such a tiny difference unnoticed, but it is easily visible in the animation.
According to Martin Gardner, this task has invented amateur magician from New York, Paul Curry in 1953. However, the principle laid down in it, was known in the 1860s. You can see that the sides of the figures given task length (2, 3, 5, 8, 13) are successive Fibonacci numbers.
via www.novate.ru/blogs/110316/35420/