563
Завдання, що тільки уважні люди можуть вирішити
Веб-сайт Запрошує вас відволікати себе від всіх речей і спробувати вирішити проблему на логіці. Розчин дуже простий, просто потрібно уважно дивитися на малюнку.
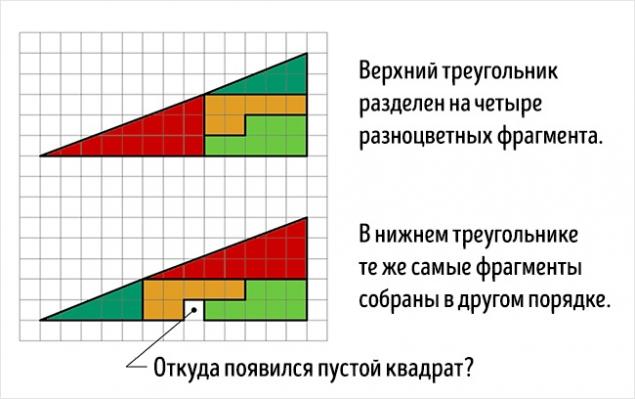
Це два трикутники. Верхній поділений без залишків на 4 фрагменти, пофарбовані різними кольорами. У нижньому трикутнику в іншому порядку розміщені однакові фрагменти. Увага, питання: Де порожньої площі приходять з?
Знайти відповідь
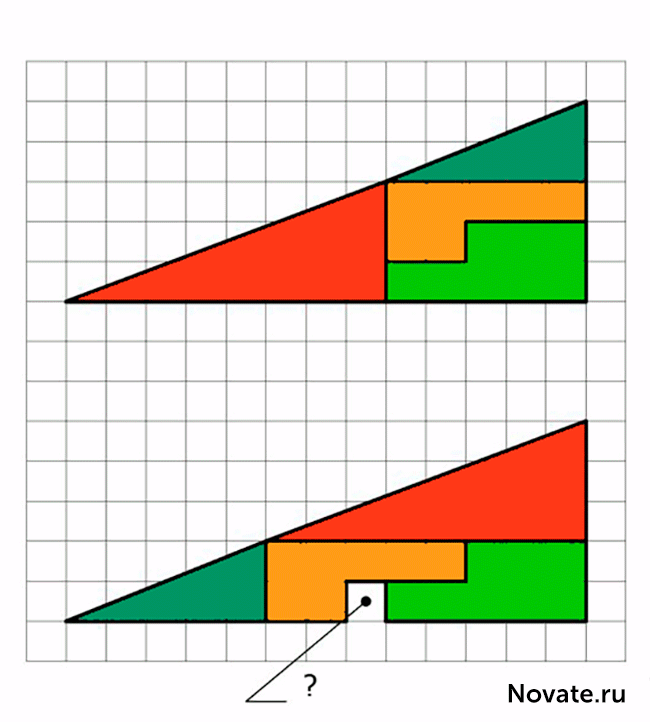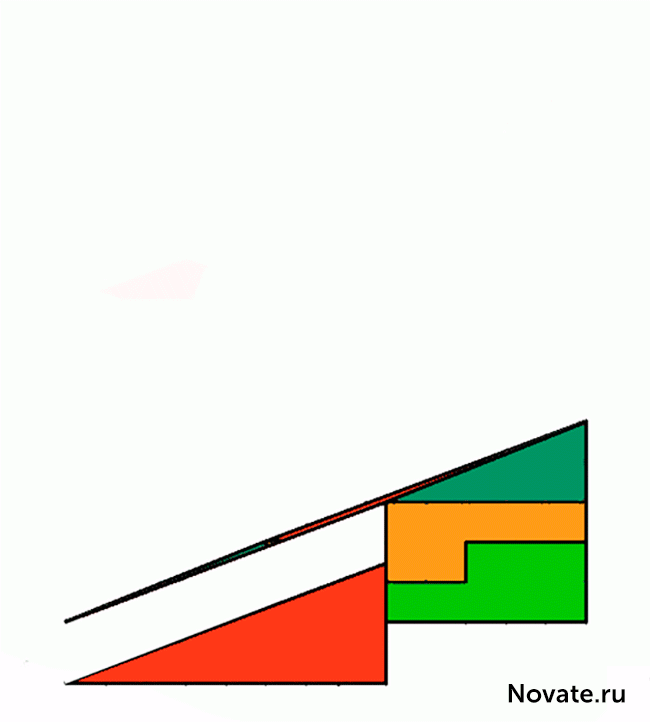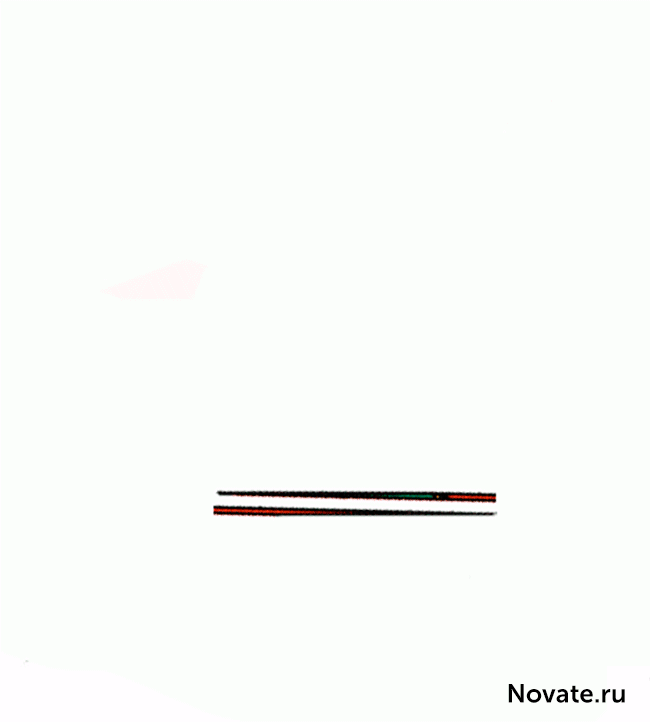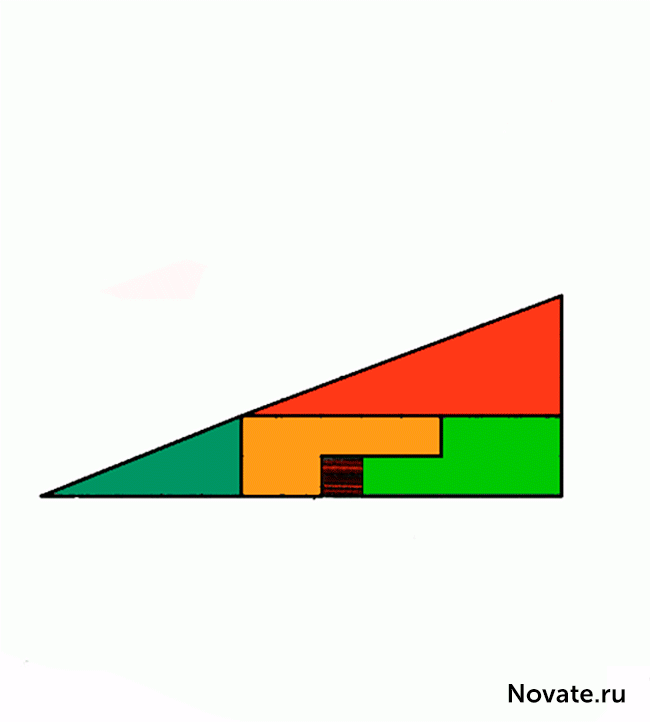
Насправді це не оптичне сприйняття, але цікава проблема. Територія пофарбованих фігур, звичайно, рівні один до (32 клітин), але що візуально спостерігається як трикутники 13 × 5, по суті, не така і має різних зон (S 13 × 5 = 32,5 клітин). Що таке, що помилка вдається в стані проблеми полягає в тому, що початкова фігура називається трикутником (це насправді притискний чотирикутник). Це добре видно на схемі нижче, де «гіпотенузи» верхніх і нижніх фігур проходять через різні точки: зверху (8,3) і внизу (5,2). Секрет лежить в властивостей синього і червоного трикутників. Легко перевіряти розрахунки.
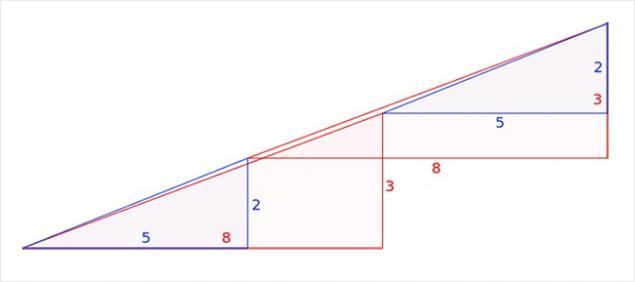
Довжина співвідношення сторін синього і червоного трикутників не дорівнює один одному (2/3 і 5/8), тому ці трикутники не схожі, і тому мають різні кути при їх відповідних вершин. Дозволяємо перший малюнок, який являє собою скріплений чотирикутник, а другий малюнок, який являє собою конденсатний восьмикутник, псевтрикутники. Якщо нижні сторони цих псевдотрикутників паралельні, то гіпотенуси в обох псевдотрикутах 13×5 фактично розбиваються лінії (в верхній частині фігури перелом створюється всередину, а в нижній фігурі - вихідні). Якщо ви надіпсуєте верхні і нижні фігурки 13 × 5 один на одного, то між ними утворюється паралелограма, яка містить «вихід» область. На схемі дана паралелограма в правильній пропорції.
Різкий кут в цьому паралелограмі дорівнює дуги 46 ≈ 0°1'18.2 ". На цьому куті хвилина рука на робочому годиннику зміщується в 12.45 секунд. Це за такою величиною, що кут нахилу в паралелограмі відрізняється від розширеної. Візуально, така невелика відмінність неприпустимо, але добре видно на анімації.
За словами Мартіна Гарднера, ця проблема була винайдена недосвідченою ілюзіоністом з Нью-Йорка, Павла Куррі, в 1953 році. Однак принцип, властивий йому, був відомий як на початку 1860-х років. Можна побачити, що бічні довжини фігур у цій задачі (2, 3, 5, 8, 13) є послідовними номерами Fibonacci.
по www.novate.ru/blogs/110316/35420/

Це два трикутники. Верхній поділений без залишків на 4 фрагменти, пофарбовані різними кольорами. У нижньому трикутнику в іншому порядку розміщені однакові фрагменти. Увага, питання: Де порожньої площі приходять з?
Знайти відповідь

Насправді це не оптичне сприйняття, але цікава проблема. Територія пофарбованих фігур, звичайно, рівні один до (32 клітин), але що візуально спостерігається як трикутники 13 × 5, по суті, не така і має різних зон (S 13 × 5 = 32,5 клітин). Що таке, що помилка вдається в стані проблеми полягає в тому, що початкова фігура називається трикутником (це насправді притискний чотирикутник). Це добре видно на схемі нижче, де «гіпотенузи» верхніх і нижніх фігур проходять через різні точки: зверху (8,3) і внизу (5,2). Секрет лежить в властивостей синього і червоного трикутників. Легко перевіряти розрахунки.

Довжина співвідношення сторін синього і червоного трикутників не дорівнює один одному (2/3 і 5/8), тому ці трикутники не схожі, і тому мають різні кути при їх відповідних вершин. Дозволяємо перший малюнок, який являє собою скріплений чотирикутник, а другий малюнок, який являє собою конденсатний восьмикутник, псевтрикутники. Якщо нижні сторони цих псевдотрикутників паралельні, то гіпотенуси в обох псевдотрикутах 13×5 фактично розбиваються лінії (в верхній частині фігури перелом створюється всередину, а в нижній фігурі - вихідні). Якщо ви надіпсуєте верхні і нижні фігурки 13 × 5 один на одного, то між ними утворюється паралелограма, яка містить «вихід» область. На схемі дана паралелограма в правильній пропорції.
Різкий кут в цьому паралелограмі дорівнює дуги 46 ≈ 0°1'18.2 ". На цьому куті хвилина рука на робочому годиннику зміщується в 12.45 секунд. Це за такою величиною, що кут нахилу в паралелограмі відрізняється від розширеної. Візуально, така невелика відмінність неприпустимо, але добре видно на анімації.
За словами Мартіна Гарднера, ця проблема була винайдена недосвідченою ілюзіоністом з Нью-Йорка, Павла Куррі, в 1953 році. Однак принцип, властивий йому, був відомий як на початку 1860-х років. Можна побачити, що бічні довжини фігур у цій задачі (2, 3, 5, 8, 13) є послідовними номерами Fibonacci.
по www.novate.ru/blogs/110316/35420/