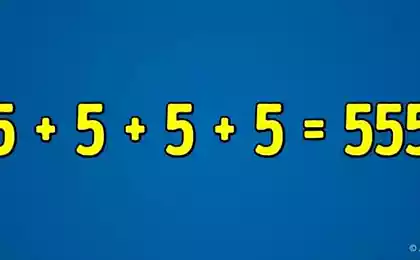861
П'ять дитячих головоломок, які вносяться в пастор для дорослих
Важко вірити, але розв'язання цих проблем у маленьких дітей займає всього 5-10 хвилин, а дорослі проводять години на них, і часто не впораються з ними взагалі! Який секрет?
Веб-сайт Публікуємо п'ять відомих завдань, які дивно легко для дітей.
У середині 2014 року на базі Гонконгу набули популярності "віральних" Її рішення у шестирічної дитини зазвичай займає не більше 20 секунд, але непідготовлені дорослі вона часто входить до складу.
Яка кількість прихована під автомобілем?

Рішення: Як часто справа в таких випадках проблема з дорослими полягає в тому, що вони збираються занадто важко — наприклад, намагаючись розрахувати візерунок, за яким розташовані номери парковок. В реальності картина просто повинна бути розумовою.
Інше математика
Відома проблема, яка дошкільняється в 5-10 хвилин. Для деяких програмістів це займає до години, і багато людей, які зареєстрували кілька аркушів паперу, додають.
Рішення: Молоді діти не можуть робити рівняння або шукати математичні візерунки, тому вони помітили, що значення залежить від кількості кола в кожній цифрі. На 9, одне коло, на 8 - два, на 1 - ні, і, отже, 2581 = 2.
Ця проблема має хороший аналог:
1 = 5
2 = 25
3 = 125
4 = 625
5 = ?
Відома проблема в якому остаточне питання значно складніше, ніж стан.
У сумці немає ні цукерки. Шість з них помаранчеві. Решта жовта. Hannah takes цукерки з її мішок і з'їдає його. Потім він знову бере ще один і з'їдає. Імовірність, що вона ate два помаранчеві цукерки 1/3. Випробувано, що n2-n-90 = 0.
Неприємний кінець історії Ганни захопив безліч жартів онлайн. Вона сказала: «Ханна ate деякі цукерки». Розрахувати окружність еквалайзера Юпітера з кальмаром і іржіючою ложкою. й
Рішення: Багато канатів не в змозі знайти рішення, тому що вони переконані, що n потрібно обчислювати спочатку, але це не дуже необхідно.
Імовірність Ганна витягуючи апельсинову цукерку вперше становить 6/n (мішок містить шість помаранчевих з n цукерок). Якщо перший раз Ганна затягувала апельсинову цукерку, ймовірність витягування того ж на другий раз становить 5/(n-1). Імовірність витягування двох помаранчевих цукерок є продуктом цих двох ймовірностей.
Ми отримуємо: (6/n)·(5/(n-1)=1⁄3. Досить спрощувати рівняння.
Де їде автобус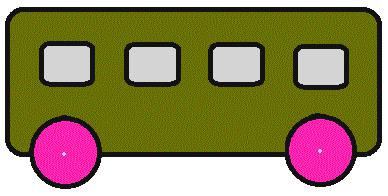
Ми можемо самі зателефонувати одержувачу і узгодити зручний час і місце вручення квітів, а якщо необхідно, то збережемо сюрприз. Де їде автобус?
Рішення: Як правило, дорослі, дивляться схематичне зображення, миттєво забути про деталі. У США діти часто приймають автобус до школи, тому вони знають, яка сторона дверей і як вона там отримує. Вони розуміють, що картина не має дверей. Так автобус пішов зліва. Звичайно, варіант, який він повертає назад, не вважається.
Для пацієнта існує ще одна вірусна проблема. За словами The Guardian, в'єтнамський вчитель дає йому вісім років дітям, і вони справляються. У той же час, навіть люди з докторантом в економіці і математикою не можуть давати рішення в короткий час.
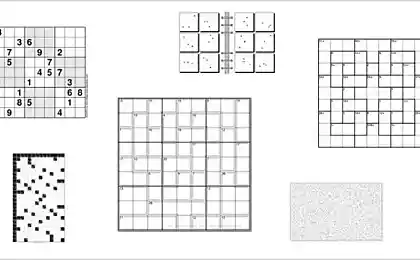
Необхідно заповнити порожні клітинки з цифрами від 1 до 9, щоб вираз було правильним.
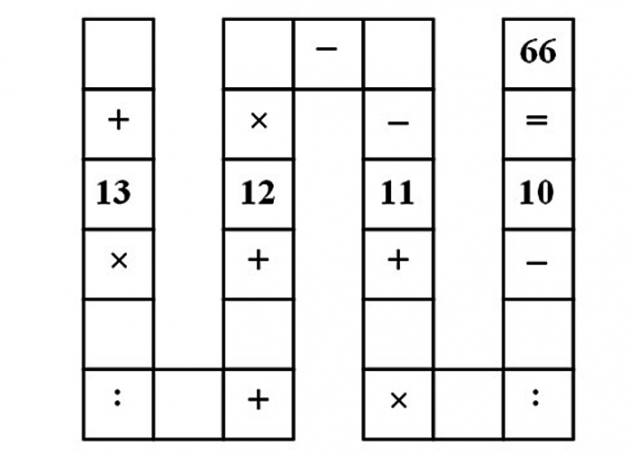
Рішення: За допомогою цієї проблеми діти навчаються запам'ятати порядок, в якому виконуються дії доповнення, відведення, багатозастосування і поділ. На жаль, в цьому випадку немає елегантного і швидкого вирішення проблеми.
Ви повинні почати писати таблицю як рівняння:
+ (g·h/i) - 10 = 66
А потім доведіть його до вигляду:
+1 ad - f + (13·b/c) + 12·e + (g·h/i) = 87
Це може бути припустимо, що b/c і gh/i повинні бути цілими, і 13·b/c не повинен бути занадто великим. На цьому етапі багато людей воліють писати програму, але якщо ви хочете, ви можете просто пройти через сотні варіантів.
Діти зазвичай вирішують, щоб мінімізувати 13·b/c, б повинні бути 2, і c повинні бути 1.
Ось ми йдемо.
+ до +12
Діти потім розуміють, що вони повинні позбутися від 3,5 і 7, які викликають труднощі поділу, і призначити ці значення, д і f, відповідно.
Підсумок: 12e +(gh/i) = 60
Трохи грати з рештою чисел ви можете знайти те, що e = 4, g = 9, h = 8, i = 6.
Таким чином, діти вирішують цю проблему, якщо вони завжди дотримуються найпростішої доріжки, і дорослі, які шукають лову від життя, часто не справляються з нею.
через tjournal.ru/p/known-tasks
Веб-сайт Публікуємо п'ять відомих завдань, які дивно легко для дітей.
У середині 2014 року на базі Гонконгу набули популярності "віральних" Її рішення у шестирічної дитини зазвичай займає не більше 20 секунд, але непідготовлені дорослі вона часто входить до складу.
Яка кількість прихована під автомобілем?

Рішення: Як часто справа в таких випадках проблема з дорослими полягає в тому, що вони збираються занадто важко — наприклад, намагаючись розрахувати візерунок, за яким розташовані номери парковок. В реальності картина просто повинна бути розумовою.
Інше математика

Відома проблема, яка дошкільняється в 5-10 хвилин. Для деяких програмістів це займає до години, і багато людей, які зареєстрували кілька аркушів паперу, додають.
Рішення: Молоді діти не можуть робити рівняння або шукати математичні візерунки, тому вони помітили, що значення залежить від кількості кола в кожній цифрі. На 9, одне коло, на 8 - два, на 1 - ні, і, отже, 2581 = 2.
Ця проблема має хороший аналог:
1 = 5
2 = 25
3 = 125
4 = 625
5 = ?
Відома проблема в якому остаточне питання значно складніше, ніж стан.
У сумці немає ні цукерки. Шість з них помаранчеві. Решта жовта. Hannah takes цукерки з її мішок і з'їдає його. Потім він знову бере ще один і з'їдає. Імовірність, що вона ate два помаранчеві цукерки 1/3. Випробувано, що n2-n-90 = 0.
Неприємний кінець історії Ганни захопив безліч жартів онлайн. Вона сказала: «Ханна ate деякі цукерки». Розрахувати окружність еквалайзера Юпітера з кальмаром і іржіючою ложкою. й
Рішення: Багато канатів не в змозі знайти рішення, тому що вони переконані, що n потрібно обчислювати спочатку, але це не дуже необхідно.
Імовірність Ганна витягуючи апельсинову цукерку вперше становить 6/n (мішок містить шість помаранчевих з n цукерок). Якщо перший раз Ганна затягувала апельсинову цукерку, ймовірність витягування того ж на другий раз становить 5/(n-1). Імовірність витягування двох помаранчевих цукерок є продуктом цих двох ймовірностей.
Ми отримуємо: (6/n)·(5/(n-1)=1⁄3. Досить спрощувати рівняння.
Де їде автобус

Ми можемо самі зателефонувати одержувачу і узгодити зручний час і місце вручення квітів, а якщо необхідно, то збережемо сюрприз. Де їде автобус?
Рішення: Як правило, дорослі, дивляться схематичне зображення, миттєво забути про деталі. У США діти часто приймають автобус до школи, тому вони знають, яка сторона дверей і як вона там отримує. Вони розуміють, що картина не має дверей. Так автобус пішов зліва. Звичайно, варіант, який він повертає назад, не вважається.
Для пацієнта існує ще одна вірусна проблема. За словами The Guardian, в'єтнамський вчитель дає йому вісім років дітям, і вони справляються. У той же час, навіть люди з докторантом в економіці і математикою не можуть давати рішення в короткий час.
Необхідно заповнити порожні клітинки з цифрами від 1 до 9, щоб вираз було правильним.

Рішення: За допомогою цієї проблеми діти навчаються запам'ятати порядок, в якому виконуються дії доповнення, відведення, багатозастосування і поділ. На жаль, в цьому випадку немає елегантного і швидкого вирішення проблеми.
Ви повинні почати писати таблицю як рівняння:
+ (g·h/i) - 10 = 66
А потім доведіть його до вигляду:
+1 ad - f + (13·b/c) + 12·e + (g·h/i) = 87
Це може бути припустимо, що b/c і gh/i повинні бути цілими, і 13·b/c не повинен бути занадто великим. На цьому етапі багато людей воліють писати програму, але якщо ви хочете, ви можете просто пройти через сотні варіантів.
Діти зазвичай вирішують, щоб мінімізувати 13·b/c, б повинні бути 2, і c повинні бути 1.
Ось ми йдемо.
+ до +12
Діти потім розуміють, що вони повинні позбутися від 3,5 і 7, які викликають труднощі поділу, і призначити ці значення, д і f, відповідно.
Підсумок: 12e +(gh/i) = 60
Трохи грати з рештою чисел ви можете знайти те, що e = 4, g = 9, h = 8, i = 6.
Таким чином, діти вирішують цю проблему, якщо вони завжди дотримуються найпростішої доріжки, і дорослі, які шукають лову від життя, часто не справляються з нею.
через tjournal.ru/p/known-tasks