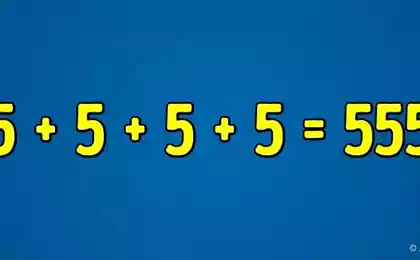Five children's puzzles, which are introduced into a stupor adults

It's hard to believe, but in the solution of these problems in young children takes only 5-10 minutes, while adults spend hours on them and often do not can cope with them! Guess what is the secret?

Website publishes five known problems that children are amazingly easy.

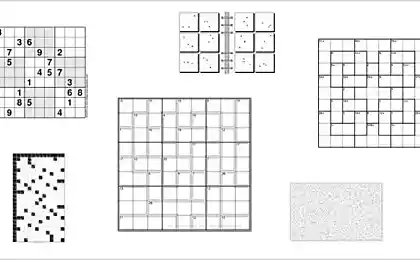
parking space number h2> The task for Hong Kong students who scored "viral" popularity in the mid-2014. On her decision to have a six-year child usually takes no more than 20 seconds, but the untrained adult, she often enters into a stupor.

Which number is hidden under the car?





Solution: as often happens in such cases, the problem of adults is that they are way too complicated - for example, trying to calculate the pattern according to which the number of parking spaces are located. In reality, the picture you just have to turn the mind.

Other math h2>

A well-known problem that preschoolers decide for 5-10 minutes. Some programmers spent on it up to an hour, and many people fill a few sheets of paper, shall be.

Solution: small children can not make the equation or look for mathematical patterns, so they notice that the value depends on the number of dots in each digit. In one circle 9, 8 - two in one - a single, and therefore 2581 = 2.

In this task, there is a good analogue:

1 = 5
2 = 25
3 = 125
4 = 625
5 =?

Hannah and sharply increased complexity h2> Famous task meme in which the final question seems much more difficult than the condition.

The bag of candy n. Six of them orange. The rest - yellow. Hannah takes a piece of candy from a bag and eats. Then takes another one and again eats. The probability that she ate two orange candy - 1/3. Prove that n²-n-90 = 0.

blockquote> The strange story of Hannah gave birth to the completion of the network a lot of jokes. The most famous: "Hannah ate some chocolates. Calculate the circumference of the equator of Jupiter using tracing paper and a rusty spoon ».

Solution: Many netizens can not find a solution, because they are convinced that it is necessary to first calculate n, but in reality this is not required.

The probability that the first time Hanna pulled sweet orange - 6 / n (in a bag of six orange candy n). If the first time Hanna pulled sweet orange, then the probability of drawing the same second time - 5 / (n-1). Chance pull two orange candy - the product of these two probabilities.

We obtain: (6 / n) ⋅ (5 / (n-1)) = ¹/₃. Then enough to simplify the equation.

Where bus rides h2>

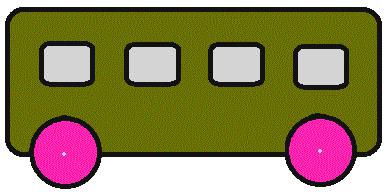
Mocking a simple task that falls to all the collections of this kind of puzzles - understandable for children and adults incomprehensible. Where bus rides?

Solution: are usually adults, seeing a diagram instantly forget about the details. In the US, children often go to school on the bus, so they know which side of his door, and he arrives. They realize that the picture is not enough doors. So, the bus goes to the left. Of course, an option that he rents ago, is not considered.

for patient h2> Yet another "viral" task. According to The Guardian, the Vietnamese teacher gives her an eight children, and they cope. In this solution in a short time we could not give even people with a doctorate degree in economics and mathematics.

It is necessary to fill the empty cells with numbers from 1 to 9 so that the expression was true.





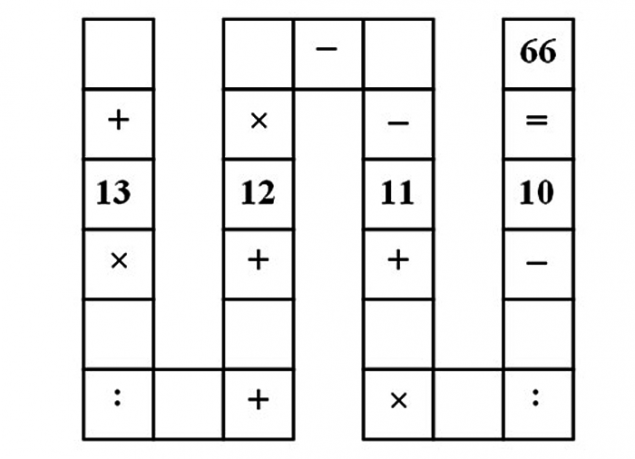
Solution: with this puzzles, children are taught to memorize the order in which made the operations of addition, subtraction, multiplication and division. Unfortunately, in this case, the problem is not some kind of elegant and quick solution.

We must start by writing the table in the form of the equation:

a + (13⋅b / c) + d + 12⋅e - f - 11 + (g⋅h / i) - 10 = 66

Then bring it to mind:

a + d - f + (13⋅b / c) + 12⋅e + (g⋅h / i) = 87

It can be assumed that b / c and gh / i must be integers, and 13⋅b / c should not be too large. At this stage, many people prefer to write a program, but if you want you can just go through about a hundred options.

Children usually decide what to minimize 13⋅b / c, b should be equal to 2, and c - 1.

Get:

a + d - f + 12e + (gh / i) = 61

Then the children understand that they need to get rid of the 3, 5 and 7, causing difficulties in the division, and assign these values ​​a, d and f, respectively.

Outcome: 12e + (gh / i) = 60

Play a little with the remaining numbers, you can find out what e = 4, g = 9, h = 8, i = 6.

Thus children solve this puzzle, if you always go the simplest way, and adults looking for a trick of life, it often can not cope.



via tjournal.ru/p/famous-tasks