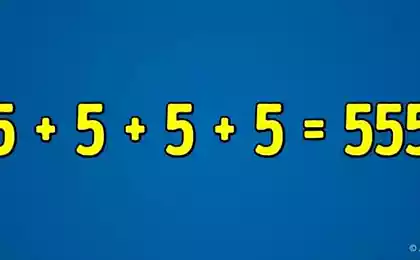Rompecabezas Cinco de los niños, que se introducen en un estupor adultos
Sitio web publica cinco problemas conocidos que los niños son increíblemente fácil.
Número de plaza de aparcamiento h2> La tarea para los estudiantes de Hong Kong que obtuvieron popularidad "viral" en el mediados de 2014. En su decisión de tener un hijo de seis años por lo general no toma más de 20 segundos, pero el adulto no entrenado, que a menudo entra en un estado de estupor.
¿Qué número se oculta bajo el coche?

Solución: como suele ocurrir en estos casos, el problema de los adultos es que son demasiado complicado - por ejemplo, tratando de calcular el patrón según el cual se encuentra el número de plazas de aparcamiento. En realidad, la imagen sólo tienes que girar la mente.
Otros matemáticas h2> 
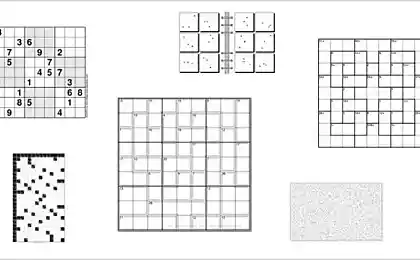
Un problema bien conocido que los preescolares deciden durante 5-10 minutos. Algunos programadores gastado en ella hasta una hora, y muchas personas se llenan unas cuantas hojas de papel, será.
Solución: los niños pequeños no pueden hacer la ecuación o buscar patrones matemáticos, por lo que notar que el valor depende del número de puntos en cada dígito. En un círculo de 9, 8 - dos en uno - una sola, por lo que 2581 = 2.
En esta tarea, hay una buena analógica:
1 = 5
2 = 25
3 = 125
4 = 625
5 =?
Hannah y marcadamente mayor complejidad h2> meme tarea famoso en el que la pregunta final parece mucho más difícil que la condición.
La bolsa de dulces n. Seis de ellos naranja. El resto - amarillo. Hannah toma un pedazo de caramelo de una bolsa y come. Luego toma otra y otra vez come. La probabilidad de que comía de dos caramelos de naranja - 1/3. Demostrar que n²-n-90 = 0.
Blockquote> La extraña historia de Hannah dio a luz a la finalización de la red un montón de chistes. El más famoso: "Hannah comió algunos chocolates. Calcula la circunferencia del ecuador de Júpiter usando papel de calco y una cuchara oxidada ».
Solución: Muchos internautas no puede encontrar una solución, porque están convencidos de que es necesario primero calcular n, pero en realidad esto no es necesario
.
La probabilidad de que la primera vez que Hanna sacó naranja dulce - 6 / n (en una bolsa de seis naranjas dulces n). Si la primera vez Hanna sacó de naranja dulce, entonces la probabilidad de sacar el mismo segundo tiempo - 5 / (n-1). Probabilidad tirar de dos caramelos de naranja - el producto de estas dos probabilidades
.
Obtenemos: (6 / n) ⋅ (5 / (n-1)) = ¹ / ₃. Entonces lo suficiente como para simplificar la ecuación.
¿Dónde viajes en autobús h2>
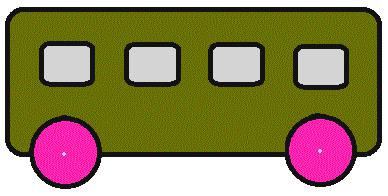
Burlarse de una tarea sencilla que cae a todas las colecciones de este tipo de rompecabezas - comprensibles para los niños y adultos incomprensibles. Cuando viajes en autobús?
Solución: son por lo general los adultos, al ver un diagrama instante olvidarse de los detalles. En los EE.UU., los niños a menudo van a la escuela en el autobús, para que sepan de qué lado de la puerta, y él llega. Se dan cuenta de que la imagen no es suficiente puertas. Así, el bus va a la izquierda. Por supuesto, una opción que hace que alquila, no se considera.
para pacientes h2> otra tarea "viral". Según The Guardian, el maestro vietnamita le da un ocho hijos, y hacer frente. En esta solución en un corto período de tiempo que no podíamos dar incluso las personas con un doctorado en economía y matemáticas.
Es necesario llenar las celdas vacías con números del 1 al 9 de modo que la expresión era cierto.
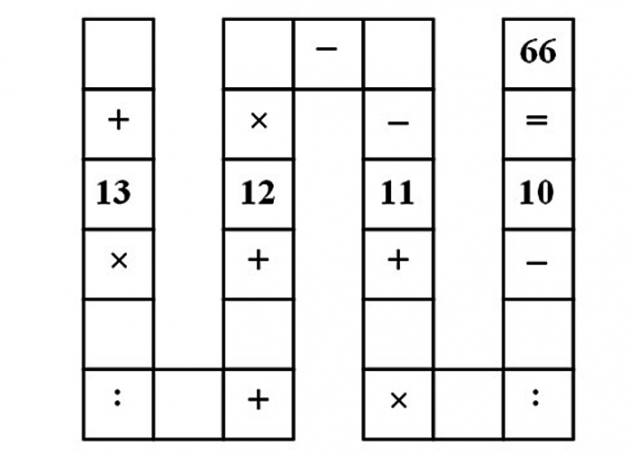
Solución: con este rompecabezas, los niños se les enseña a memorizar el orden en el que realizó las operaciones de suma, resta, multiplicación y división. Por desgracia, en este caso, el problema no es algún tipo de solución elegante y rápido.
Debemos empezar por escribir la mesa en forma de la ecuación:
a + (13⋅b / c) + d + 12⋅e - f - 11 + (g⋅h / i) - 10 = 66
Entonces traerlo a la mente:
a + d - f + (13⋅b / c) + 12⋅e + (g⋅h / i) = 87
Se puede suponer que b / cy gh / i deben ser enteros, y 13⋅b / c no debe ser demasiado grande. En esta etapa, muchas personas prefieren escribir un programa, pero si quieres puedes ir a través de un centenar de opciones.
Los niños por lo general deciden qué minimizar 13⋅b / c, b debe ser igual a 2, y c - 1.
Get:
a + d - f + 12e + (gh / i) = 61
Entonces los niños comprendan que tienen que deshacerse de los 3, 5 y 7, causando dificultades en la división, y asignar estos valores a, D y F, respectivamente.
Resultado: 12e + (gh / i) = 60
Juega un poco con los números restantes, puede averiguar lo que e = 4 g = 9, h = 8, i = 6.
De este modo los niños a resolver este rompecabezas, si siempre va la manera más simple, y los adultos que buscan un truco de la vida, a menudo no puede hacer frente.
a través de tjournal.ru/p/famous-tasks