860
0.2
2015-11-05
Пять детских головоломок, которые вводят в ступор взрослых
В это трудно поверить, но на решение этих задач у маленьких детей уходит всего по 5–10 минут, а взрослые тратят на них часы, а нередко и вообще не могут с ними справиться! Догадайтесь, в чём секрет?
Сайт публикует пять известных задач, которые поразительно легко даются детям.
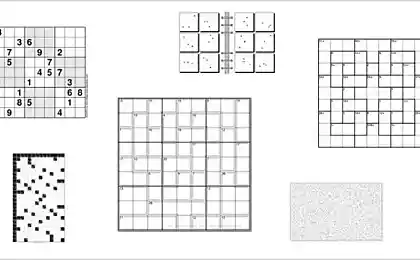
Какое число скрыто под машиной?

Решение: как часто бывает в подобных случаях, проблема взрослых заключается в том, что они идут слишком сложным путём — например, пытаются высчитать закономерность, согласно которой расположены номера парковочных мест. В действительности же картинку надо просто мысленно перевернуть.

Известная задача, которую дошкольники решают за 5–10 минут. У некоторых программистов уходит на неё до часа, а многие люди, исписав несколько листов бумаги, сдаются.
Решение: маленькие дети не могут составлять уравнения или искать математические закономерности, поэтому они замечают, что значение зависит от количества кружочков в каждой цифре. В 9 один кружочек, в 8 — два, в 1 — ни одного, а, значит, 2581=2.
У этой задачи есть хороший аналог:
1 = 5
2 = 25
3 = 125
4 = 625
5 = ?
Решение: многие пользователи сети никак не могут найти решение, потому что убеждены, что для него нужно сначала вычислить n, однако в действительности этого не требуется.
Вероятность того, что в первый раз Ханна вытянула оранжевую конфету — 6/n (в сумке шесть оранжевых из n конфет). Если в первый раз Ханна вытянула оранжевую конфету, то вероятность вытянуть такую же во второй раз — 5/(n-1). Вероятность вытянуть две оранжевые конфеты — произведение этих двух вероятностей.
Получаем: (6/n)⋅(5/(n-1))=¹⁄₃. Дальше достаточно упростить уравнение.
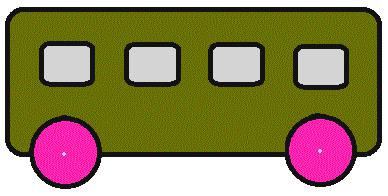
Издевательски простая задача, которая попадает во все сборники такого рода головоломок — понятных детям и непонятных взрослым. Куда едет автобус?
Решение: обычно взрослые, видя схематичное изображение, мигом забывают о деталях. В США дети часто ездят в школу на автобусе, поэтому знают, с какой стороны у него двери и как он подъезжает. Они понимают, что на картинке не хватает дверей. Значит, автобус едет влево. Само собой, вариант, что он сдаёт назад, не рассматривается.
Нужно заполнить пустые клетки числами от 1 до 9, так чтобы выражение было верным.
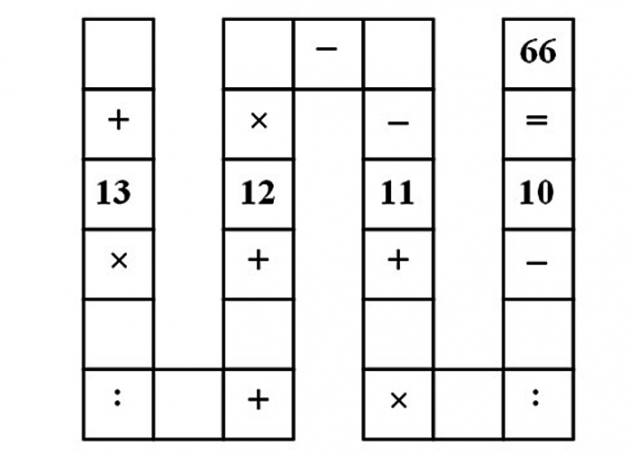
Решение: с помощью этой задачки детей учат запоминать порядок, в котором производятся действия сложения, вычитания, умножения и деления. К сожалению, в данном случае у проблемы нет какого-то изящного и быстрого решения.
Начать следует, записав таблицу в виде уравнения:
a + (13⋅b/c) + d + 12⋅e — f — 11 + (g⋅h/i)- 10 = 66
А затем привести его к виду:
a + d — f + (13⋅b/c) + 12⋅e +(g⋅h/i) = 87
Можно предположить, что b/c и gh/i должны быть целыми, а 13⋅b/c не должно быть слишком большим. На этом этапе многие предпочитают написать программу, однако при желании можно просто перебрать около сотни вариантов.
Дети обычно решают, что для минимизации 13⋅b/c, b должно быть равно 2, а c — 1.
Получаем:
a + d — f + 12e +(gh/i) = 61
Затем дети понимают, что им необходимо быстрее избавиться от 3,5 и 7, вызывающих сложности при делении, и присваивают эти значения a, d и f соответственно.
Итог: 12e +(gh/i) = 60
Немного поигравшись с оставшимися цифрами, можно выяснить, что e=4, g=9, h=8, i=6.
Таким образом дети решают эту задачку, если всегда идут по самому простому пути, а взрослые, ищущие от жизни подвоха, с ней зачастую не справляются.
via tjournal.ru/p/famous-tasks
Сайт публикует пять известных задач, которые поразительно легко даются детям.
Номер парковочного места
Задачка для гонконгских школьников, которая набрала «вирусную» популярность в середине 2014 года. На её решение у шестилетнего ребёнка обычно уходит не больше 20 секунд, а вот неподготовленных взрослых она часто вводит в ступор.Какое число скрыто под машиной?

Решение: как часто бывает в подобных случаях, проблема взрослых заключается в том, что они идут слишком сложным путём — например, пытаются высчитать закономерность, согласно которой расположены номера парковочных мест. В действительности же картинку надо просто мысленно перевернуть.
Другая математика

Известная задача, которую дошкольники решают за 5–10 минут. У некоторых программистов уходит на неё до часа, а многие люди, исписав несколько листов бумаги, сдаются.
Решение: маленькие дети не могут составлять уравнения или искать математические закономерности, поэтому они замечают, что значение зависит от количества кружочков в каждой цифре. В 9 один кружочек, в 8 — два, в 1 — ни одного, а, значит, 2581=2.
У этой задачи есть хороший аналог:
1 = 5
2 = 25
3 = 125
4 = 625
5 = ?
Ханна и резко повышенная сложность
Знаменитая задачка-мем, в которой итоговый вопрос кажется куда более сложным, чем условие.В сумке n конфет. Шесть из них оранжевые. Остальные — жёлтые. Ханна берёт конфету из сумки и съедает. Затем берёт ещё одну и снова съедает. Вероятность того, что она съела две оранжевые конфеты — 1/3. Докажите, что n²-n-90=0.Странное завершение истории Ханны породило в сети множество шуток. Самая известная: «Ханна съела несколько конфет. Рассчитайте длину окружности экватора Юпитера с помощью кальки и ржавой ложки».
Решение: многие пользователи сети никак не могут найти решение, потому что убеждены, что для него нужно сначала вычислить n, однако в действительности этого не требуется.
Вероятность того, что в первый раз Ханна вытянула оранжевую конфету — 6/n (в сумке шесть оранжевых из n конфет). Если в первый раз Ханна вытянула оранжевую конфету, то вероятность вытянуть такую же во второй раз — 5/(n-1). Вероятность вытянуть две оранжевые конфеты — произведение этих двух вероятностей.
Получаем: (6/n)⋅(5/(n-1))=¹⁄₃. Дальше достаточно упростить уравнение.
Куда едет автобус

Издевательски простая задача, которая попадает во все сборники такого рода головоломок — понятных детям и непонятных взрослым. Куда едет автобус?
Решение: обычно взрослые, видя схематичное изображение, мигом забывают о деталях. В США дети часто ездят в школу на автобусе, поэтому знают, с какой стороны у него двери и как он подъезжает. Они понимают, что на картинке не хватает дверей. Значит, автобус едет влево. Само собой, вариант, что он сдаёт назад, не рассматривается.
Для терпеливых
Ещё одна «вирусная» задачка. Как сообщает The Guardian, вьетнамский учитель даёт её восьмилетним детям, и они справляются. При этом решения за короткое время не смогли дать даже люди с докторской степенью по экономике и математике.Нужно заполнить пустые клетки числами от 1 до 9, так чтобы выражение было верным.

Решение: с помощью этой задачки детей учат запоминать порядок, в котором производятся действия сложения, вычитания, умножения и деления. К сожалению, в данном случае у проблемы нет какого-то изящного и быстрого решения.
Начать следует, записав таблицу в виде уравнения:
a + (13⋅b/c) + d + 12⋅e — f — 11 + (g⋅h/i)- 10 = 66
А затем привести его к виду:
a + d — f + (13⋅b/c) + 12⋅e +(g⋅h/i) = 87
Можно предположить, что b/c и gh/i должны быть целыми, а 13⋅b/c не должно быть слишком большим. На этом этапе многие предпочитают написать программу, однако при желании можно просто перебрать около сотни вариантов.
Дети обычно решают, что для минимизации 13⋅b/c, b должно быть равно 2, а c — 1.
Получаем:
a + d — f + 12e +(gh/i) = 61
Затем дети понимают, что им необходимо быстрее избавиться от 3,5 и 7, вызывающих сложности при делении, и присваивают эти значения a, d и f соответственно.
Итог: 12e +(gh/i) = 60
Немного поигравшись с оставшимися цифрами, можно выяснить, что e=4, g=9, h=8, i=6.
Таким образом дети решают эту задачку, если всегда идут по самому простому пути, а взрослые, ищущие от жизни подвоха, с ней зачастую не справляются.
via tjournal.ru/p/famous-tasks
Портал БАШНЯ. Копирование, Перепечатка возможна при указании активной ссылки на данную страницу.