562
只有思想的人可以决定的任务
网站 STRONG>为您提供除了所有的情况下,并尝试解决逻辑谜题。解决的办法很简单,你只需要在图像仔细观察。搜索结果
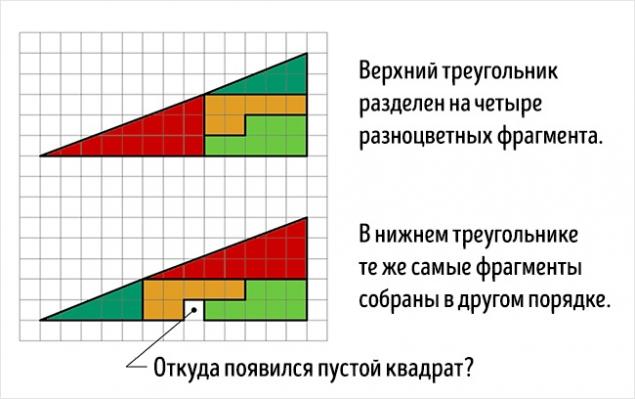
中国 你两个三角形前。顶部均匀地分成4个片段,喷涂各种颜色。相同的部分的下三角布置成不同的顺序。注意的问题:?哪儿来的多余的空白框 STRONG>
中国学习正确的答案搜索结果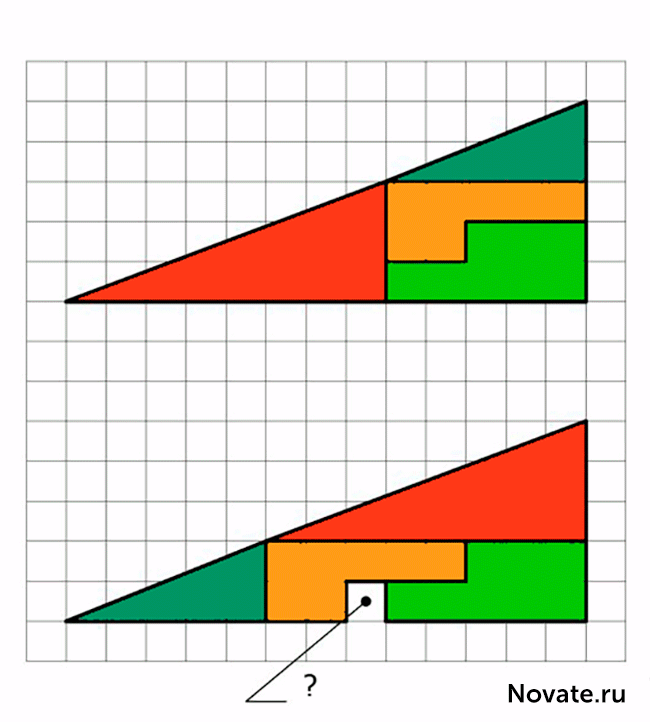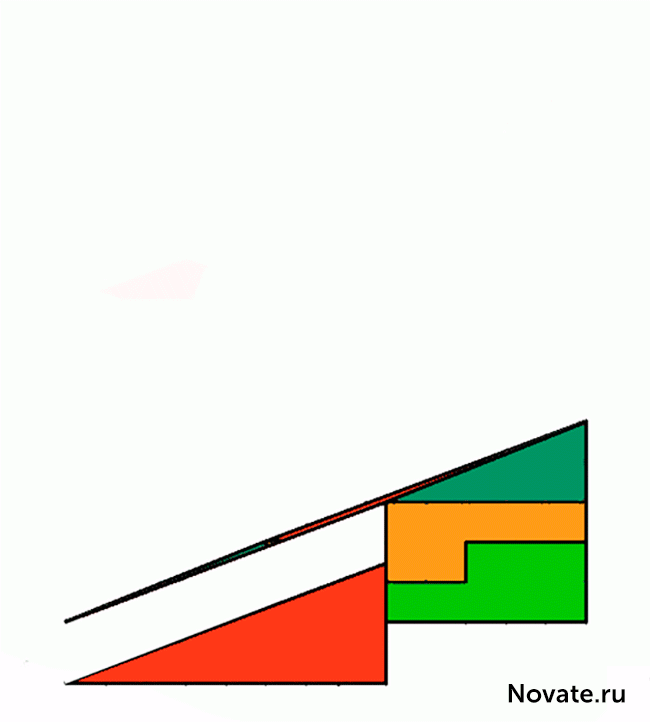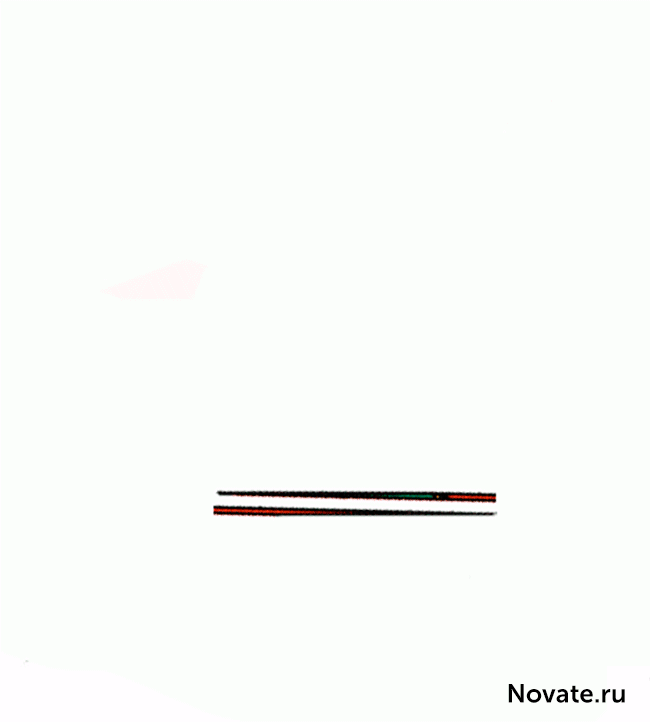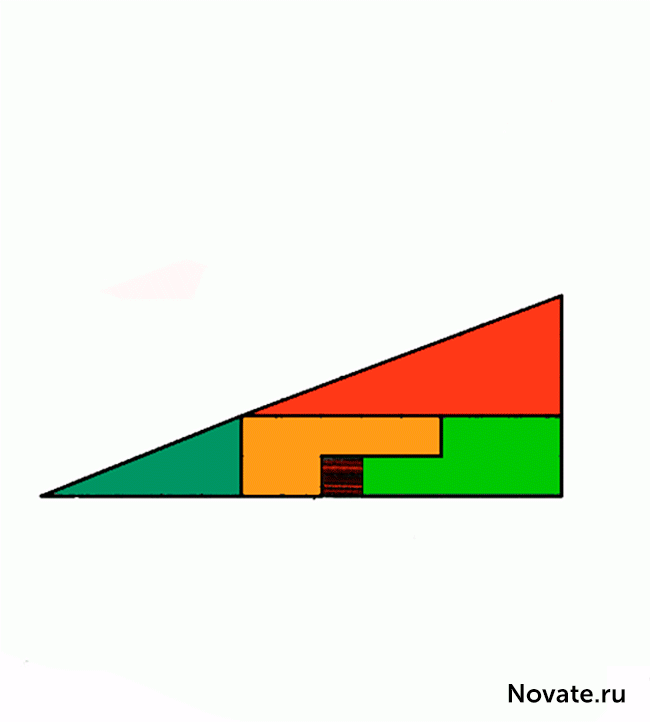
中国 在现实中,这是不是一种错觉,但有趣的任务。当然,阴影图中的面积相等(32个细胞),但作为三角形×13 5实际上是不即使这样具有不同的区域被目视观察(S 13 = 5×32 5细胞)。这是一个错误,在这个问题伪装的,是最初的数字称为三角形(实际上它是一个凹四边形)。这是在下面的图图,其中,上部和下部片的“斜边”通过不同点清楚明显:在顶部(8,3)和所述底部(5,2)。秘密 - 在蓝色和红色三角形的性质。这很容易检查计算。搜索结果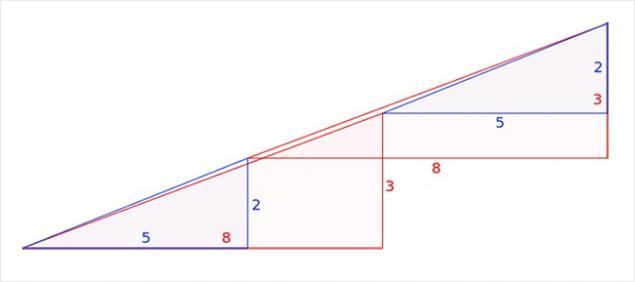
中国 各方关系有关蓝色和红色三角形的长度是不相等的(2/3和5/8),所以三角形不相似,因此,有在各顶点不同的角度。我们说,第一图形是一个凹四边形,而第二个数字是凹八角形,psevdotreugolnikami。如果平行这些psevdotreugolnikov的下部,然后在这两个斜边psevdotreugolnikah 13×5实际上是虚线(上图内创建一个突破,并在底部 - 出)。如果我们施加的顶部和底部件13×5彼此形成了“斜边”平行四边形,并且它包含在“额外”区之间。图图这个平行四边形的正确比例给出。搜索结果 平行四边形的锐角是46 arcctg≈0°1'18,2“。在这个角度分针的健康小时轮班12,45秒。它是在这样的在此平行四边形钝角值不同于扩展。在视觉上如此微小的差异被忽视,但它是在动画清晰可见。搜索结果 据马丁·加德纳,这项任务在1953年发明了业余魔术师从纽约,保罗·库里。但是,原则就定下来了,在19世纪60年代是众所周知的。你可以看到,给定的任务长度(2,3,5,8,13)的数字双方都连续的斐波那契数。
中国
中国
中国
中国 通过www.novate.ru/blogs/110316/35420/

中国 你两个三角形前。顶部均匀地分成4个片段,喷涂各种颜色。相同的部分的下三角布置成不同的顺序。注意的问题:?哪儿来的多余的空白框 STRONG>
中国学习正确的答案搜索结果

中国 在现实中,这是不是一种错觉,但有趣的任务。当然,阴影图中的面积相等(32个细胞),但作为三角形×13 5实际上是不即使这样具有不同的区域被目视观察(S 13 = 5×32 5细胞)。这是一个错误,在这个问题伪装的,是最初的数字称为三角形(实际上它是一个凹四边形)。这是在下面的图图,其中,上部和下部片的“斜边”通过不同点清楚明显:在顶部(8,3)和所述底部(5,2)。秘密 - 在蓝色和红色三角形的性质。这很容易检查计算。搜索结果

中国 各方关系有关蓝色和红色三角形的长度是不相等的(2/3和5/8),所以三角形不相似,因此,有在各顶点不同的角度。我们说,第一图形是一个凹四边形,而第二个数字是凹八角形,psevdotreugolnikami。如果平行这些psevdotreugolnikov的下部,然后在这两个斜边psevdotreugolnikah 13×5实际上是虚线(上图内创建一个突破,并在底部 - 出)。如果我们施加的顶部和底部件13×5彼此形成了“斜边”平行四边形,并且它包含在“额外”区之间。图图这个平行四边形的正确比例给出。搜索结果 平行四边形的锐角是46 arcctg≈0°1'18,2“。在这个角度分针的健康小时轮班12,45秒。它是在这样的在此平行四边形钝角值不同于扩展。在视觉上如此微小的差异被忽视,但它是在动画清晰可见。搜索结果 据马丁·加德纳,这项任务在1953年发明了业余魔术师从纽约,保罗·库里。但是,原则就定下来了,在19世纪60年代是众所周知的。你可以看到,给定的任务长度(2,3,5,8,13)的数字双方都连续的斐波那契数。
中国
中国
中国
中国 通过www.novate.ru/blogs/110316/35420/