563
La tarea que sólo las personas inteligentes pueden decidir
< Sitio Web le ofrece, aparte de todos los casos y tratar de resolver el rompecabezas de la lógica. La solución es muy simple, sólo tiene que mirar de cerca la imagen.
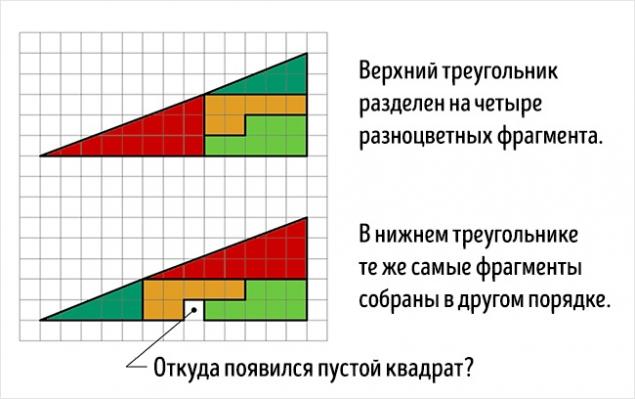
Antes de usted dos triángulos. Top uniformemente divididos en 4 fragmentos, pintado en diferentes colores. El triángulo inferior de las mismas secciones están dispuestas en un orden diferente. La atención a la pregunta :? donde hizo la casilla en blanco adicional
Aprender la respuesta correcta
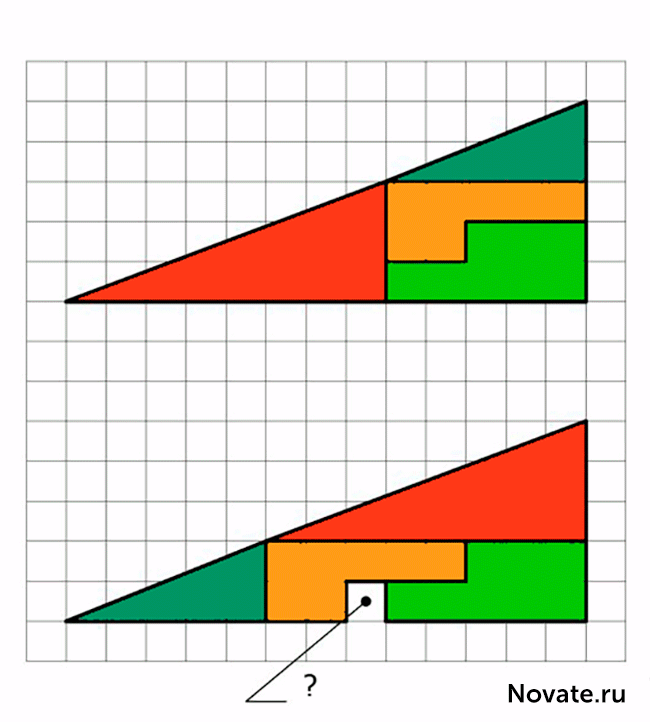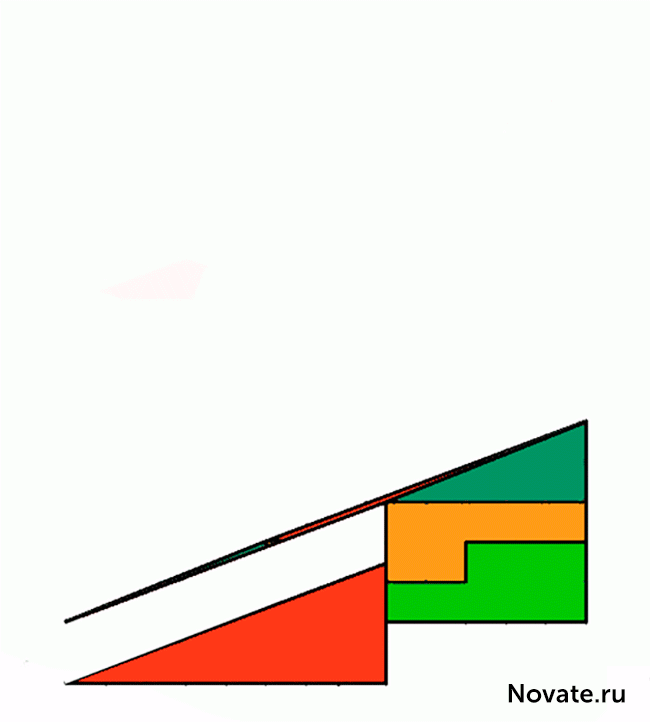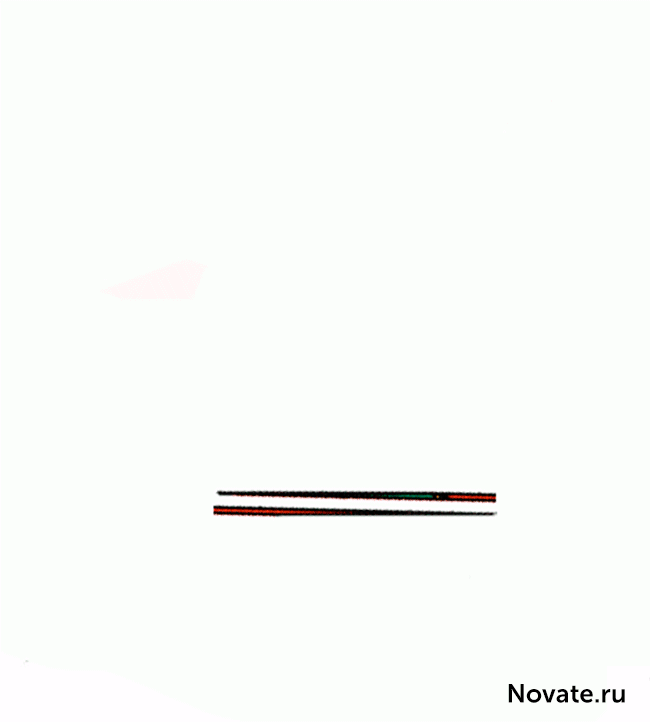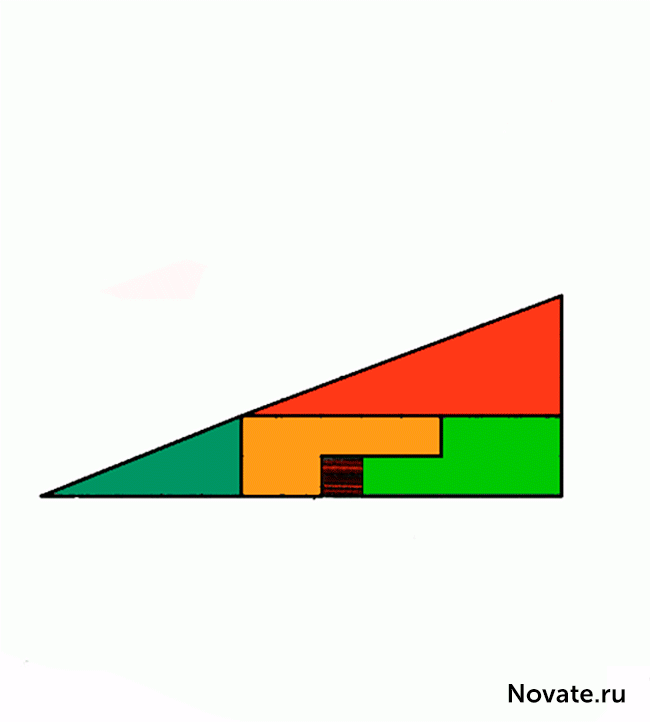
En realidad, esto no es una ilusión óptica, pero tarea interesante. por supuesto, las áreas sombreadas figuras son iguales (32 células), pero que se observa visualmente como triángulos × 13 5, de hecho, ni siquiera es como tal tiene diferentes áreas (S 13 = 5 × 32 5 células). Eso es un error, disfrazado con el problema, es que la cifra inicial llama un triángulo (de hecho, es un cuadrilátero cóncavo). Esto es claramente evidente en el diagrama siguiente figura, donde el "hipotenusa" de las piezas superior e inferior pase a través de diferentes puntos: en la parte superior (8, 3) y el fondo (5, 2). El secreto - en las propiedades de los triángulos azules y rojas. Es fácil de comprobar los cálculos.
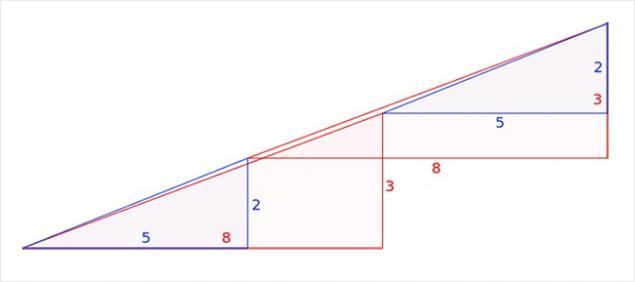
Relación entre las partes se refería a longitudes de triángulos azules y rojas no son iguales (2/3 y 5/8), por lo que los triángulos no son similares y, por lo tanto, tienen diferentes ángulos en los vértices respectivos. Decimos que la primera cifra es un cuadrilátero cóncavo, y la segunda cifra es octógono cóncavo, psevdotreugolnikami. Si la parte inferior de éstas psevdotreugolnikov paralelo, entonces la hipotenusa tanto en psevdotreugolnikah 13 × 5 líneas son en realidad rotas (la cifra superior crea una ruptura en el interior, y en la parte inferior - out). Si imponemos las piezas superior e inferior 13 × 5 entre sí, entre su paralelogramo "hipotenusas" formada, y que está contenido en el área de "extra". Figura gráfico de este paralelogramo se da en proporciones correctas.
El ángulo agudo del paralelogramo es 46 arcctg ≈ 0 ° 1'18, 2 ". En este ángulo de la aguja de los minutos en los turnos sana horas para 12, 45 segundos. Es en un valor de ángulo obtuso tal en este paralelogramo es diferente de expandido. Visualmente una pequeña diferencia tan desapercibido, pero es fácilmente visible en la animación.
Según Martin Gardner, esta tarea ha inventado mago aficionado de Nueva York, Paul Curry en 1953. Sin embargo, el principio establecido en el mismo, fue conocido en la década de 1860. Se puede ver que los lados de las cifras indicadas longitud de tareas (2, 3, 5, 8, 13) son números de Fibonacci sucesivos.
a través de www.novate.ru/blogs/110316/35420/

Antes de usted dos triángulos. Top uniformemente divididos en 4 fragmentos, pintado en diferentes colores. El triángulo inferior de las mismas secciones están dispuestas en un orden diferente. La atención a la pregunta :? donde hizo la casilla en blanco adicional
Aprender la respuesta correcta

En realidad, esto no es una ilusión óptica, pero tarea interesante. por supuesto, las áreas sombreadas figuras son iguales (32 células), pero que se observa visualmente como triángulos × 13 5, de hecho, ni siquiera es como tal tiene diferentes áreas (S 13 = 5 × 32 5 células). Eso es un error, disfrazado con el problema, es que la cifra inicial llama un triángulo (de hecho, es un cuadrilátero cóncavo). Esto es claramente evidente en el diagrama siguiente figura, donde el "hipotenusa" de las piezas superior e inferior pase a través de diferentes puntos: en la parte superior (8, 3) y el fondo (5, 2). El secreto - en las propiedades de los triángulos azules y rojas. Es fácil de comprobar los cálculos.

Relación entre las partes se refería a longitudes de triángulos azules y rojas no son iguales (2/3 y 5/8), por lo que los triángulos no son similares y, por lo tanto, tienen diferentes ángulos en los vértices respectivos. Decimos que la primera cifra es un cuadrilátero cóncavo, y la segunda cifra es octógono cóncavo, psevdotreugolnikami. Si la parte inferior de éstas psevdotreugolnikov paralelo, entonces la hipotenusa tanto en psevdotreugolnikah 13 × 5 líneas son en realidad rotas (la cifra superior crea una ruptura en el interior, y en la parte inferior - out). Si imponemos las piezas superior e inferior 13 × 5 entre sí, entre su paralelogramo "hipotenusas" formada, y que está contenido en el área de "extra". Figura gráfico de este paralelogramo se da en proporciones correctas.
El ángulo agudo del paralelogramo es 46 arcctg ≈ 0 ° 1'18, 2 ". En este ángulo de la aguja de los minutos en los turnos sana horas para 12, 45 segundos. Es en un valor de ángulo obtuso tal en este paralelogramo es diferente de expandido. Visualmente una pequeña diferencia tan desapercibido, pero es fácilmente visible en la animación.
Según Martin Gardner, esta tarea ha inventado mago aficionado de Nueva York, Paul Curry en 1953. Sin embargo, el principio establecido en el mismo, fue conocido en la década de 1860. Se puede ver que los lados de las cifras indicadas longitud de tareas (2, 3, 5, 8, 13) son números de Fibonacci sucesivos.
a través de www.novate.ru/blogs/110316/35420/