数学解决了费米 - 意大利面 - 乌拉姆问题

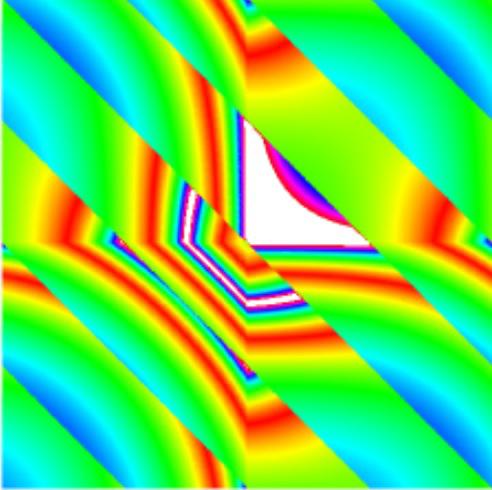
一组科学家为首的数学理工学院Rensellera尤里·利沃夫教授设法找到费米面食 - 乌拉姆（FPU）的一个很好的解决方案，在1953年首次制定，被认为是实验数学的根本问题之一。

FPU问题 - 第一次尝试，以验证统计力学定律应用到非线性系统具有足够大数量的自由度中的一个。

在科学论文发表 在杂志美国国家科学研究院 i>的论文集。它提供了所需的能量，以产生在群众由字符串，它倾向于热平衡连接的链中的一个全波什么水平的数学解释。体32（或颗粒）只能向左或向右移动，并且该系统的能量不能由摩擦或热耗散。

当在1953年，科学家们已经制定了这个问题，他们认为这将有可能找到通过计算在计算机上的解决方案。计算数学数字积分计算机（MANIAC），是世界第一台数字计算机1启动。然而，人们发现，后的能量的多次迭代周期性消散在系统中，并作为其结果的能量的97％集中在一个主体。也就是说，在热平衡还没有实现。这种现象被称为“复发FPU”还是引起了很多的问题，他是数百篇科学论文的主题。

经过几十年的使用功能更强大的计算机，数学仍然设法运行在该系统达到热平衡仿真，但问题是力量在身体如何准确分布。在科学工作“路线在α-费米面食 - 乌拉姆系统热化”尤里·利沃夫和他的同事提供了一个优雅的回答这个问题。在能源的时候逐渐转移他们的主要过程时相同的六个州在系统中。然后能量被不可逆地转移。具有大量的重合六种状态迭代时刻有的足够次数，以便被发送足够的能量，以达到热平衡。

来源： geektimes.ru/post/247758/