921
Mathematics solved the problem of the Fermi-Pasta-Ulam
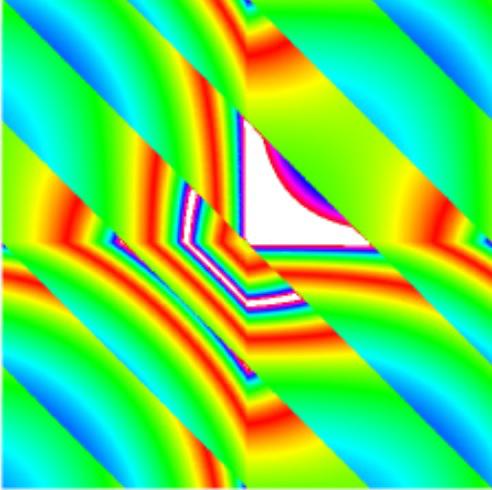
A group of scientists led by Professor of Mathematics Polytechnic Institute Rensellera Yuri Lvov managed to find an elegant solution of the Fermi-Pasta-Ulam (FPU), first formulated in 1953 and is considered one of the fundamental problems of experimental mathematics.
FPU problem - one of the first attempts to verify the application of the laws of statistical mechanics to a nonlinear system with a sufficiently large number of degrees of freedom.
The scientific article published in the journal Proceedings of the National Academy of Science i>. It provides a mathematical explanation of what level of energy required to produce one full wave in the chain of masses connected by strings, which tend to thermal equilibrium. Body 32 (or particles) can only move left or right, and energy of the system can not be dissipated by friction or heat.
When in 1953, scientists have formulated this problem, they thought it would be possible to find a solution by calculating on the computer. Calculation launched on Mathematical Numerical Integrator and Computer (MANIAC), one of the first digital computers in the world. However, it was found that after many iterations of the energy dissipated in the system periodically, and as a result 97% of the energy is concentrated in one body. That is, the thermal equilibrium has not been achieved. A phenomenon known as "relapse FPU" still causes a lot of questions, and he was the subject of hundreds of scientific papers.
After decades of using more powerful computers, mathematics still managed to run the simulation in which the system reaches thermal equilibrium, but the question remains how the exact distribution of power over the bodies. In scientific work "Route to thermalization in the α-Fermi-Pasta-Ulam system" Yuri Lvov and colleagues offer an elegant answer to this question. Their main procedure in a gradual transfer of energy at the time when the same six states in the system. Then the energy is transferred irreversibly. With a large number of iterations moments of coincidence six states there are a sufficient number of times, so that sufficient energy is transmitted to reach thermal equilibrium.
Source: geektimes.ru/post/247758/
In Australia, found the crash site of the largest meteorite in the history of the planet
Kick in the future - bipedal robot walks and falls