657
How to determine the unknown: Fermi method for rapid assessment of anything
To develop the ability to measure the unknown is not a simple matter. Fortunately, history has known many individuals who have demonstrated a striking ability. One of them is Nobel prize winner in physics, who taught his students to measure-for example, estimating the number of piano tuners in Chicago.
1. How to identify an unknown
In physics Enrico Fermi (1901-1954), received in 1938 the Nobel prize, was a real talent for intuitive dimensions, even sometimes seemingly random. Once he demonstrated it at the atomic bomb test at Trinity site on 16 July 1945, which, together with other scientists-nuclear scientists were observing the blast from base camp.
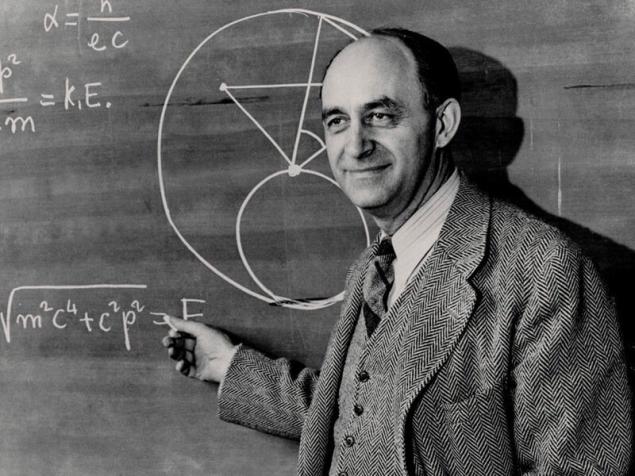
While others have finally configured the devices for measuring the power of the explosion, Fermi tore into small pieces a page from his notebook. After the explosion, a strong wind blew, he threw the pieces into the air and see where they fell (fragments emitted on the far side, had to show the peak of the pressure wave). Fermi came to the conclusion that the power of the blast wave exceeds 10 kilotons.
This information was very important, as other observers the lower limit of this parameter was unknown. After a long analysis of readings the power of the blast was eventually estimated at 18.6 kilotons.
Fermi was able to determine the correct factor, having one simple observation — the scattering of the scraps of paper in the wind.
Fermi was famous for the fact that taught students skills to approximate calculations of the most fantastic values that they could not have any idea. The most famous example of such a "Fermi question" is a determination of the number of piano tuners in Chicago.
Students (future scientists and engineers) started with the fact that they do not calculate any data. Of course, you could just count all the Adjusters, after reading the ads, to cope in any Agency that issues licenses for such services, etc. But Fermi was trying to teach their students to solve problems and when to check the result. He wanted them to understand that still know something about the desired quantity.
For starters Fermi was asked to identify other relevant to pianos and their Adjusters indicators is also unknown, but it is easier to assess. It was the population of Chicago (formed in 1930-1950-ies, over 3 million people), the average number of persons per family (two or three), the percentage of households that regularly use the services of piano tuners (the most — one in ten, minimally every third family), the desired tuning frequency (on average probably at least once a year), the number of pianos, custom-Adjuster for the day (four or five instruments taking into account the cost of time on the road), as well as the number of working days of an Adjuster of the year (for example, 250).
These data allowed us to calculate the number of the Adjusters according to the following formula:
The number of piano tuners in Chicago =
= (Population / Number of members of the same family) x
x the Percentage of families who use the services of Adjusters x
x Number of options in a year /
/ (The number of pianos, custom one Adjuster per day x Number of working days in a year).
Depending on numbers, we substitute in this equation, you will get an answer in the range of 20-200; the correct answer was approximately 50 people. When this figure is compared with the real (which Fermi could learn from a telephone directory), she was always closer to real than I thought by the students.
The resulting interval of values too much, but isn't this a huge step forward compared to the position of "is it even possible to define?", which students took at the beginning?
This approach allowed conducting calculations for people to understand the origin of the uncertainty. Which variables were characterized by the greatest uncertainty — the percentage of households that regularly use the services of piano tuners, frequency settings, the number of tools that you can configure for the day, or something else? The largest source of uncertainty indicated which dimensions will minimize it.
The search for the answer to "Fermi" doesn't involve new observations and, therefore, cannot unconditionally be considered as a dimension. Rather, it is an assessment of what you already know about the problem in a way that few come close to the target.
Here is another lesson for the businessman do not consider the uncertainty of the unavoidable and not amenable to analysis. Instead of to become despondent about their ignorance, ask yourself: what you do know about the problem? Assessment of available quantitative information on the subject is a very important stage of measure phenomena that seem immeasurable.
2. "Fermi questions" for the new company
Chuck Mackay from the company Wizard of Ads encourages the use of "Fermi questions" to estimate the size your market in a particular area. Recently, one insurance agent asked Chuck to give advice, whether of his company to open an office in Wichita falls (Texas), where until now she had no representation.
Whether in this market the demand for the services of another insurer? To verify the feasibility of the plan, Mackay used the method of "Fermi questions" and started with the problem of population.
According to public statistics, residents of Wichita falls owned 62 172 vehicles, and the average annual car insurance premium in Texas was 837,40 dollars. Mackay suggested that almost all cars are insured, because this is a mandatory requirement.
Therefore, total revenue from insurance was $ 52 annually 062 833 dollars. The agent learned that the average Commission rate is 12%, so that all of the annual Commission fee amounted to $ 6 247 $ 540. In the city there were 38 insurance agencies. If you divide all commissions of 38 agencies, it appears that the annual fees of one of them, on average, 164 409 USD.
The market, apparently, was already saturated, as the population of Wichita falls was reduced from 104 to 197 people in 2000 to 99 846 people in 2005. in addition, the market has already worked for several large firms, therefore, the income of the new Agency would be even less — all without the overhead cost.
Conclusion Mackay: most likely, a new Agency in this city is unlikely to be profitable, so the plan should be abandoned.
3. What can we learn from the example of the Fermi
Managers often say: "anything like that we could not even guess." They give in to uncertainty. Instead of trying to take measurements, they are inactive, discouraged by the seeming impossibility of eliminating it. Fermi in such a case, could say: "Yes, you don't know much, but what you do know?"
Other managers argue: "to determine this figure, you need to spend millions". In the end, they prefer not to carry out smaller-scale (low-cost) research, because their accuracy is usually higher than those of expensive integrated scientific papers.
Meanwhile, even a small reduction in uncertainty can be worth millions depending on the importance of the decision, the adoption of which it facilitates, and the frequency of such decisions.
Also interesting: As bought and sold Your lack of confidence
The degradation of the brain — to read ALL!
"Fermi questions" showed even far from science people as possible to carry out measurements that seem at first glance, so complex that it is not worth trying to deal with them. Usually things that are considered in the business measurable, you can quantify with simple tricks of observation, as soon as people realize that the immeasurability is an illusion.
From this point of view, the value of the Fermi approach consists primarily in the fact that the assessment of the current level of our knowledge about the subject is a necessary condition for subsequent measurements.published
Author: Douglas W. Hubbard (Douglas W. Hubbard)
P. S. And remember, just changing your mind — together we change the world! ©
Join us in Facebook , Vkontakte, Odnoklassniki
Source: www.elitarium.ru/metod-fermi-ocenka-izmerenie-neopredelennost-reshenie-primer-navyk/
1. How to identify an unknown
In physics Enrico Fermi (1901-1954), received in 1938 the Nobel prize, was a real talent for intuitive dimensions, even sometimes seemingly random. Once he demonstrated it at the atomic bomb test at Trinity site on 16 July 1945, which, together with other scientists-nuclear scientists were observing the blast from base camp.

While others have finally configured the devices for measuring the power of the explosion, Fermi tore into small pieces a page from his notebook. After the explosion, a strong wind blew, he threw the pieces into the air and see where they fell (fragments emitted on the far side, had to show the peak of the pressure wave). Fermi came to the conclusion that the power of the blast wave exceeds 10 kilotons.
This information was very important, as other observers the lower limit of this parameter was unknown. After a long analysis of readings the power of the blast was eventually estimated at 18.6 kilotons.
Fermi was able to determine the correct factor, having one simple observation — the scattering of the scraps of paper in the wind.
Fermi was famous for the fact that taught students skills to approximate calculations of the most fantastic values that they could not have any idea. The most famous example of such a "Fermi question" is a determination of the number of piano tuners in Chicago.
Students (future scientists and engineers) started with the fact that they do not calculate any data. Of course, you could just count all the Adjusters, after reading the ads, to cope in any Agency that issues licenses for such services, etc. But Fermi was trying to teach their students to solve problems and when to check the result. He wanted them to understand that still know something about the desired quantity.
For starters Fermi was asked to identify other relevant to pianos and their Adjusters indicators is also unknown, but it is easier to assess. It was the population of Chicago (formed in 1930-1950-ies, over 3 million people), the average number of persons per family (two or three), the percentage of households that regularly use the services of piano tuners (the most — one in ten, minimally every third family), the desired tuning frequency (on average probably at least once a year), the number of pianos, custom-Adjuster for the day (four or five instruments taking into account the cost of time on the road), as well as the number of working days of an Adjuster of the year (for example, 250).
These data allowed us to calculate the number of the Adjusters according to the following formula:
The number of piano tuners in Chicago =
= (Population / Number of members of the same family) x
x the Percentage of families who use the services of Adjusters x
x Number of options in a year /
/ (The number of pianos, custom one Adjuster per day x Number of working days in a year).
Depending on numbers, we substitute in this equation, you will get an answer in the range of 20-200; the correct answer was approximately 50 people. When this figure is compared with the real (which Fermi could learn from a telephone directory), she was always closer to real than I thought by the students.
The resulting interval of values too much, but isn't this a huge step forward compared to the position of "is it even possible to define?", which students took at the beginning?
This approach allowed conducting calculations for people to understand the origin of the uncertainty. Which variables were characterized by the greatest uncertainty — the percentage of households that regularly use the services of piano tuners, frequency settings, the number of tools that you can configure for the day, or something else? The largest source of uncertainty indicated which dimensions will minimize it.
The search for the answer to "Fermi" doesn't involve new observations and, therefore, cannot unconditionally be considered as a dimension. Rather, it is an assessment of what you already know about the problem in a way that few come close to the target.
Here is another lesson for the businessman do not consider the uncertainty of the unavoidable and not amenable to analysis. Instead of to become despondent about their ignorance, ask yourself: what you do know about the problem? Assessment of available quantitative information on the subject is a very important stage of measure phenomena that seem immeasurable.
2. "Fermi questions" for the new company
Chuck Mackay from the company Wizard of Ads encourages the use of "Fermi questions" to estimate the size your market in a particular area. Recently, one insurance agent asked Chuck to give advice, whether of his company to open an office in Wichita falls (Texas), where until now she had no representation.
Whether in this market the demand for the services of another insurer? To verify the feasibility of the plan, Mackay used the method of "Fermi questions" and started with the problem of population.
According to public statistics, residents of Wichita falls owned 62 172 vehicles, and the average annual car insurance premium in Texas was 837,40 dollars. Mackay suggested that almost all cars are insured, because this is a mandatory requirement.
Therefore, total revenue from insurance was $ 52 annually 062 833 dollars. The agent learned that the average Commission rate is 12%, so that all of the annual Commission fee amounted to $ 6 247 $ 540. In the city there were 38 insurance agencies. If you divide all commissions of 38 agencies, it appears that the annual fees of one of them, on average, 164 409 USD.
The market, apparently, was already saturated, as the population of Wichita falls was reduced from 104 to 197 people in 2000 to 99 846 people in 2005. in addition, the market has already worked for several large firms, therefore, the income of the new Agency would be even less — all without the overhead cost.
Conclusion Mackay: most likely, a new Agency in this city is unlikely to be profitable, so the plan should be abandoned.
3. What can we learn from the example of the Fermi
Managers often say: "anything like that we could not even guess." They give in to uncertainty. Instead of trying to take measurements, they are inactive, discouraged by the seeming impossibility of eliminating it. Fermi in such a case, could say: "Yes, you don't know much, but what you do know?"
Other managers argue: "to determine this figure, you need to spend millions". In the end, they prefer not to carry out smaller-scale (low-cost) research, because their accuracy is usually higher than those of expensive integrated scientific papers.
Meanwhile, even a small reduction in uncertainty can be worth millions depending on the importance of the decision, the adoption of which it facilitates, and the frequency of such decisions.
Also interesting: As bought and sold Your lack of confidence
The degradation of the brain — to read ALL!
"Fermi questions" showed even far from science people as possible to carry out measurements that seem at first glance, so complex that it is not worth trying to deal with them. Usually things that are considered in the business measurable, you can quantify with simple tricks of observation, as soon as people realize that the immeasurability is an illusion.
From this point of view, the value of the Fermi approach consists primarily in the fact that the assessment of the current level of our knowledge about the subject is a necessary condition for subsequent measurements.published
Author: Douglas W. Hubbard (Douglas W. Hubbard)
P. S. And remember, just changing your mind — together we change the world! ©
Join us in Facebook , Vkontakte, Odnoklassniki
Source: www.elitarium.ru/metod-fermi-ocenka-izmerenie-neopredelennost-reshenie-primer-navyk/