Sorprendente Paradojas que te llevarán a un rompecabezas

Las paradojas se pueden encontrar en todas partes, desde la ecología a la geometría y desde la lógica a la química. Incluso el ordenador que estás leyendo está lleno de paradojas. Aquí hay diez explicaciones de paradojas bastante fascinantes. Algunos de ellos son tan extraños que no podemos entender completamente cuál es el punto.

1. La paradoja Banach-Tarsky: Imagina tener una pelota. Ahora imagina que empiezas a romper esta bola en pedazos, y las piezas pueden ser cualquier forma que te guste. Pon las piezas juntas para que tengas dos bolas en vez de una. ¿Cuál será el tamaño de estas bolas en comparación con la bola original?

Según la teoría de conjuntos, las dos bolas serán del mismo tamaño y forma que la bola original. Además, dado que las bolas tienen un volumen diferente, entonces cualquiera de las bolas se puede convertir de acuerdo con el otro. Esto nos permite concluir que el guisante puede dividirse en bolas del tamaño del Sol.

El truco de la paradoja es que puedes romper las bolas en pedazos de cualquier forma. En la práctica, esto no es posible – la estructura del material y, en última instancia, el tamaño de los átomos impone algunas limitaciones.

Para que realmente sea posible desgarrar la bola de la manera que desee, debe contener un número infinito de puntos nulos-dimensionales disponibles. Entonces la bola de tales puntos será infinitamente densa, y cuando la desgarro, las formas de las piezas pueden llegar a ser tan complejas que no tendrán un cierto volumen. Y usted puede montar estas piezas, cada una que contiene un número infinito de puntos, en una nueva bola de cualquier tamaño. La nueva bola aún consistirá en puntos infinitos, y ambas bolas serán igualmente infinitamente densas. Si intentas poner la idea en práctica, no funcionará. Pero todo funciona bien al trabajar con esferas matemáticas – sets numéricos ilimitadamente divisibles en el espacio tridimensional. La paradoja resuelta se llama el teorema de Banach-Tarsky y juega un papel enorme en la teoría del conjunto matemático.

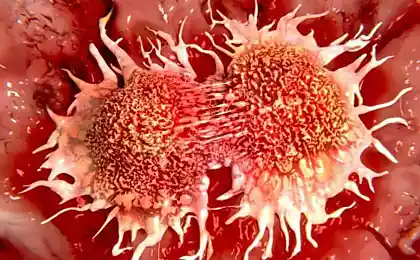
2. Obviamente, las ballenas son mucho más grandes que nosotros, lo que significa que tienen muchas más células en sus cuerpos. Cada célula en el cuerpo puede teóricamente volverse maligno. Así que las ballenas son mucho más propensos a tener cáncer que los humanos, ¿verdad?

No así. La paradoja Peto, llamada después del profesor de Oxford Richard Peto, argumenta que no hay correlación entre el tamaño animal y el cáncer. Los humanos y las ballenas tienen la misma posibilidad de tener cáncer, pero algunas razas de ratones pequeños son mucho más probables.

Algunos biólogos creen que la falta de correlación en la paradoja de Peto puede explicarse por el hecho de que los animales más grandes resisten mejor los tumores: el mecanismo funciona de tal manera que prevenga la mutación de las células en el proceso de división.

3. Para que algo exista físicamente, debe estar presente en nuestro mundo por algún tiempo. No puede haber ningún objeto sin longitud, anchura y altura, y no puede haber ningún objeto sin “duración” — un objeto “instantánea”, es decir, uno que no existe al menos por algún tiempo, no existe en absoluto.

Según el nihilismo universal, el pasado y el futuro no toman tiempo en el presente. Además, es imposible cuantificar la duración que llamamos “tiempo actual”: cualquier cantidad de tiempo que llames “tiempo actual” puede dividirse en partes – pasado, presente y futuro.

Si el presente dura, digamos, un segundo, este segundo se puede dividir en tres partes: la primera parte será el pasado, el segundo - el presente, el tercero - el futuro. Un tercio del segundo que ahora llamamos el presente también se puede dividir en tres partes. Seguramente ya has entendido la idea – puedes continuar para siempre.

Así que el presente no existe porque no continúa a tiempo. El nihilismo universal utiliza este argumento para demostrar que nada existe en absoluto.

4. Para resolver problemas que requieren un razonamiento reflexivo, las personas tienen dificultades. Por otro lado, las funciones básicas motor y sensoriales como caminar no causan ninguna dificultad en absoluto.

Pero si hablamos de computadoras, lo contrario es cierto: las computadoras son muy fáciles de resolver problemas lógicos complejos como desarrollar una estrategia de ajedrez, pero es mucho más difícil programar una computadora para que pueda caminar o reproducir el discurso humano. Esta distinción entre inteligencia natural y artificial se conoce como la paradoja Moravec. Hans Moravec, investigador del Departamento de Robótica de la Universidad Carnegie Mellon, explica esta observación a través de la idea de ingeniería inversa nuestro propio cerebro. La ingeniería inversa es la más difícil de hacer en tareas que los humanos realizan inconscientemente, como las funciones motoras.

Debido a que el pensamiento abstracto se convirtió en parte del comportamiento humano hace menos de 100.000 años, nuestra capacidad para resolver problemas abstractos es consciente. Así que es mucho más fácil para nosotros crear tecnología que emule este comportamiento. Por otro lado, no pensamos en cosas como caminar o hablar, así que conseguir inteligencia artificial para hacer lo mismo es más difícil.

5. Ley de Benford: ¿Cuál es la posibilidad de que un número al azar comience con 1? ¿O el número 3? ¿O 7? Si usted está un poco familiarizado con la teoría de la probabilidad, usted podría asumir que la probabilidad es uno en nueve, o alrededor del 11 por ciento.

Si usted mira los números reales, usted notará que 9 es mucho menos común que el 11 por ciento del tiempo. Además, muchos menos números de los esperados comienzan con “8,” pero un 30% de los números comienza con “1”. Este patrón paradójico se manifiesta en todo tipo de casos del mundo real, desde el tamaño de la población hasta los precios del stock y la longitud del río.

El físico Frank Benford destacó primero este fenómeno en 1938. Encontró que la frecuencia de un dígito aparece como una primera gota a medida que el dígito aumenta de uno a nueve. Es decir, “1” aparece como el primer dígito en alrededor del 30,1% de los casos, “2” aparece alrededor del 17,6% de los casos, “3” – alrededor del 12,5%, y así sucesivamente a “9”, actuando como el primer dígito en sólo el 4,6% de los casos.

Para entender esto, imagine que usted constantemente numera los billetes de la lotería. Cuando has numerado entradas de uno a nueve, la probabilidad de que cualquier dígito sea el primero es el 11,1%. Cuando agrega el billete número 10, la probabilidad de que un número aleatorio comience con "1" aumenta a 18.2%. Añades entradas 11 a 19, y la posibilidad de que un número de ticket comience con un "1" sigue aumentando, alcanzando el 58%. Ahora agrega el billete número 20 y sigue numerando sus entradas. La posibilidad de que un número comience con un “2” aumenta, y la probabilidad de que comience con un “1” disminuye lentamente.

La Ley de Benford no se aplica a todas las distribuciones de números. Por ejemplo, los conjuntos de números cuyo rango es limitado (altura humana o peso) no caen bajo la ley. Tampoco funciona con conjuntos que sólo tienen una o dos órdenes. Sin embargo, la ley se aplica a muchos tipos de datos. Como resultado, las autoridades pueden utilizar la ley para detectar el fraude: cuando la información proporcionada no sigue la ley de Benford, las autoridades pueden concluir que alguien inventó los datos.

6. Los genes contienen toda la información necesaria para la creación y supervivencia de un organismo. Va sin decir que los organismos complejos deben tener los genomas más complejos, pero esto no es cierto.

Las amebas unicelulares tienen genomas 100 veces más grandes que los humanos, de hecho, tienen quizás los genomas más conocidos. Y en especies muy similares, el genoma puede ser radicalmente diferente. Esta extrañeza se conoce como la paradoja C. Una toma interesante de la paradoja C es que el genoma puede ser más grande de lo necesario. Si se utilizaran todos los genomas del ADN humano, el número de mutaciones por generación sería increíblemente alto.

Los genomas de muchos animales complejos como seres humanos y primates incluyen ADN que no codifica nada. Esta enorme cantidad de ADN no utilizado, que varía mucho de criatura a criatura, parece depender de nada, lo que crea la paradoja C.

7. Imagínese una hormiga arrastrando sobre una cuerda de goma un metro de largo a una velocidad de un centímetro por segundo. Además, imagine que la cuerda estira un kilómetro cada segundo. ¿La hormiga llegará al final?

Parece lógico que una hormiga normal no sea capaz de esto, porque su velocidad es mucho menor que la velocidad a la que se estira la cuerda. Sin embargo, la hormiga eventualmente alcanzará el extremo opuesto.

Cuando una hormiga ni siquiera ha comenzado a moverse, tiene 100% de cuerda delante de ella. Después de un segundo, la cuerda se hizo mucho más grande, pero la hormiga también viajó cierta distancia, y si cuenta en porcentajes, la distancia que debe pasar, disminuyó - ya es menos del 100%, aunque no mucho.

Aunque la cuerda se estira constantemente, la distancia pequeña que viaja por la hormiga también se hace más grande. Y aunque la cuerda se alarga a un ritmo constante, el camino de la hormiga se está volviendo ligeramente más pequeño cada segundo. La hormiga sigue avanzando a una velocidad constante. Así, con cada segundo, la distancia que ya ha caminado aumenta, y la distancia que debe pasar disminuye. En porcentaje, por supuesto.

Hay una condición para que el problema tenga una solución: la hormiga debe ser inmortal. Así, la hormiga alcanzará el final en 2.8×1043.429 segundos, que es un poco más largo de lo que el universo existe.

8. El modelo depredador-prey es una ecuación que describe la situación ecológica real. Por ejemplo, el modelo puede determinar cuánto va a cambiar el número de zorros y conejos en el bosque. Supongamos que las hierbas que los conejos comen se están volviendo cada vez más abundantes en el bosque. Podemos asumir que este resultado es favorable para los conejos, porque con una abundancia de hierba, se reproducirán bien y aumentarán el número.

La paradoja del equilibrio ecológico argumenta que este no es el caso: primero, el número de conejos aumentará, pero el crecimiento de la población de conejos en un ambiente cerrado (forest) conducirá a un aumento de la población de zorros. Entonces el número de depredadores aumentará tanto que primero destruirán toda la presa, y luego morirán ellos mismos.

En la práctica, esta paradoja no se aplica a la mayoría de las especies animales, si sólo porque no viven en un ambiente cerrado, por lo que las poblaciones animales son estables. Además, los animales pueden evolucionar: por ejemplo, en nuevas condiciones, la presa tendrá nuevos mecanismos de defensa.

9. Reúne a un grupo de amigos y vea este video juntos. Cuando hayas terminado, que todos den su opinión, si el sonido aumenta o disminuye durante los cuatro tonos. Te sorprenderá lo diferente que son las respuestas.

Para entender esta paradoja, necesitas saber algo sobre notas musicales. Cada nota tiene cierta altura, que determina si escuchamos un sonido alto o bajo. La nota de la octava siguiente, superior, suena dos veces más alta que la nota de la octava anterior. Cada octava puede dividirse en dos intervalos de tritón iguales.

En el vídeo, un newt separa cada par de sonidos. En cada par, un sonido es una mezcla de las mismas notas de diferentes octavas – por ejemplo, una combinación de dos notas antes de donde uno suena más alto que el otro. Cuando el sonido en un newt se mueve de una nota a otra (por ejemplo, un sol-sharp entre dos a), es perfectamente razonable interpretar la nota como superior o inferior a la anterior.

Otra propiedad paradójica de los newts es la sensación de que el sonido está constantemente bajando, aunque el campo no cambia. En nuestro vídeo, se puede ver el efecto durante diez minutos.

10. Antes de ustedes dos vasos de agua, exactamente iguales en todos menos uno: la temperatura del agua en el vaso izquierdo es más alta que en la derecha. Coloque ambas gafas en el congelador. ¿Qué vaso congelará el agua más rápido? Usted puede decidir que en la derecha, donde el agua era originalmente más fría, pero el agua caliente se congelará más rápido que el agua a temperatura ambiente.

Este extraño efecto se llama después de un estudiante tanzano que lo observó en 1986 mientras congelaba la leche para hacer helado. Algunos de los más grandes pensadores, Aristóteles, Francis Bacon y René Descartes, han señalado previamente este fenómeno pero no han podido explicarlo. Aristóteles, por ejemplo, hipotetizó que una calidad se mejora en un ambiente opuesto a esa calidad.

El efecto Mpemba es posible debido a varios factores. El agua en un vaso de agua caliente puede ser menor, ya que algunos de ellos se evaporarán, y como resultado, menos agua debe congelarse. Además, el agua caliente contiene menos gas, lo que significa que los flujos de convección ocurrirán más fácilmente en dicho agua, por lo tanto, será más fácil congelarlo.

Otra teoría es que los vínculos químicos que mantienen las moléculas de agua juntas se debilitan. La molécula de agua consiste en dos átomos de hidrógeno unidos a un átomo de oxígeno. Cuando el agua se calienta, las moléculas se mueven ligeramente separadas, el vínculo entre ellas se debilita, y las moléculas pierden un poco de energía - esto permite que el agua caliente se enfríe más rápido que el agua fría.

Fuente: Brainstorm-blog.ru

Fuente:/usuarios/1080