令人惊讶的夸张 会让你陷入谜题

(英语).

从生态学到几何学,从逻辑学到化学学,任何地方都可以找到paradoxs. 甚至你正在读的电脑 都充满了悖论 以下是十分引人入胜的悖论的十种解释. 我们无法完全理解问题所在。

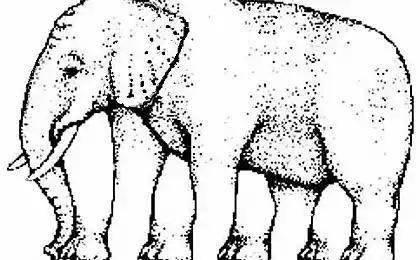
一、导 言 巴纳赫-塔尔斯基悖论: 想象一下拿着球 现在想象一下,你开始把这个球撕成碎片, 碎片可以是任何你喜欢的形状。 把棋子放在一起 这样你有两个球而不是一个 这些球与原球相比的大小是多少?

根据设定理论,两个球的大小和形状与原球相同. 此外,由于球体的体积不同,因此任何球都可以按照其他球体进行转换. 这使得我们可以得出这样的结论:豌豆可以分为太阳大小的球.

悖论的诡计在于你可以把球撕成任何形状的碎片. 在实践中,这是不可能的 — — 材料的结构以及最终原子的大小都造成了一些限制.

为了真正能够以你喜欢的方式撕裂球,它必须包含无限数量的可用的无维点. 然后这种点的球会是无限密集的,当撕裂它时,碎片的形状会变得如此复杂,以至于它们不会有一定的体积. 你可以把这些片子组装起来, 每一片都包含无限的点数, 形成一个大小不一的新球。 新球仍将由无限积分组成,两个球同样将无限密集. 如果你试图将这个想法付诸实践,那就行不通。 但是,在数学领域工作时,一切都很好 — — 在三维空间中无限分散的数字集。 解开的悖论被称为"Banach-Tarsky定理",并在数学集合理论中扮演了巨大角色.

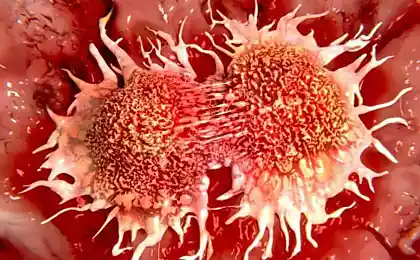
2. 国家 显然,鲸鱼比我们大得多, 这意味着它们体内的细胞要多得多。 体内的每个细胞理论上都可以变成恶性细胞. 所以鲸鱼比人类更可能得癌症,对吧?

不是那样的 以牛津教授理查德·佩托(Richard Peto)命名的佩托悖论认为,动物大小与癌症之间没有关联. 人类和鲸鱼患癌症的几率大致相同,但一些品种的小鼠更可能出现.

一些生物学家认为,佩托悖论中缺乏关联性可以解释大动物较能抵抗肿瘤的原因:这个机制发挥作用,可以防止细胞在分裂过程中发生突变.

3个 物质上存在的东西,必须存在于我们的世界中一段时间。 没有长度、宽度和高度,就不可能有物体,没有“长期”——即“瞬间”物体,即至少一段时间不存在的物体,根本不存在。

根据普遍的虚无主义,过去和将来在目前并不需要时间. 此外,我们称之为“现时”的时间是无法量化的:你称之为“现时”的任何时间都可以分为过去、现在和未来。

如果现在的,说一秒,那么这一秒可以分为三部分:第一部分是过去,第二部分是现在,第三部分是未来. 我们现在称之为现在的第二段的三分之一也可以分为三个部分。 你们确已明白这个想法,你们可以永远坚持下去。

所以现在真的不存在,因为它没有及时进行. 普遍虚无主义用这个论点来证明根本不存在.

4个 在解决需要深思熟虑的推理的问题时,人们会有困难. 另一方面,步行等基本运动和感官功能完全不会造成任何困难.

但是,如果我们谈论计算机,则恰恰相反:计算机非常容易解决复杂的逻辑问题,如开发国际象棋策略,但计算机编程更难使其能行走或复制人类的语音. 这种自然智能和人工智能的区分被称为莫拉韦克悖论. 卡内基梅隆大学机器人系研究员汉斯·莫拉韦奇(Hans Moravec)通过逆向工程我们自己的大脑来解释这个观察. 逆向工程最难完成人类无意识地执行的任务,如运动功能.

因为抽象思维在不到10万年前成为人类行为的一部分,所以我们解决抽象问题的能力是有意识的. 因此,我们更容易创造出模仿这种行为的技术。 而另一方面,我们不考虑诸如走路或说话之类的事情,因此更难获得人工智能来做同样的事情.

5.五. 本福德律法: 随机数从1开始的可能性有多大? 还是3号? 还是7? 如果你对概率理论有些熟悉, 你可能会假设概率是九分之一, 大约是11%。

如果你看看实际的数字,你会注意到9比11%的时间要少得多。 此外,从“8”开始的数字比预期的要少得多,但从“1”开始的数字却比预期的少30%。 这种自相矛盾的模式体现在各种现实世界中,从人口规模到股价和河长。

物理学家弗兰克·本福德(Frank Benford)于1938年首次注意到这一现象. 他发现,一个数字的频率随着第一个下降而出现,数字从一个增加到九个。 即"1"出现在约30.1%的病例中作为第一位数字,"2"出现在约17.6%的病例中,"3"——约12.5%,等等到"9",在只有4.6%的病例中作为第一位数字.

为了理解这一点 想象一下你一直在给彩票编号 当你把票数从1到9, 任何数字第一的机会是11.1%。 在加入10号票时,从"1"开始的随机数的概率会增加到18.2%. 加上11到19号票,从1号票开始的票号机会继续上升,最高达到58%. 现在,你加20号票 并继续编号你的票。 从“2”开始计算数字的机会增加,从“1”开始计算的可能性慢慢下降。

本福德的法律并不适用于数字的所有分布. 例如,范围有限(人的身高或体重)的几组数字不属于法律规定的范围。 它也不与只有一个或两个订单的套件合作。 然而,法律适用于许多类型的数据。 因此,当局可以使用法律来侦查欺诈行为:当所提供的信息没有遵循本福德的法律时,当局可以断定有人捏造了数据.

6个 基因包含了生物创造和生存所需的所有信息. 不言而喻,复杂的生物必须拥有最复杂的基因组,但这不是真的。

单细胞阿穆埃巴斯的基因组比人类大100倍,事实上,它们也许拥有已知最大的基因组. 在非常相似的物种中, 基因组可能完全不同。 这种怪异被称为C悖论. 从C悖论中取出的一个有趣的东西是,基因组可能大于需要. 如果人类DNA中的所有基因组都得到使用,那么每代人的突变数量会非常高。

人类和灵长类等许多复杂动物的基因组包括没有编码任何内容的DNA. 这种巨大的未使用的DNA数量,从生物到生物的差别很大,似乎不依赖于什么,这造成了C悖论.

7个 想象一只蚂蚁爬在橡胶绳上 以每秒1厘米的速度长1米 还有,想象一下绳子每秒伸一公里 蚂蚁能撑到最后吗?

正常的蚂蚁似乎无法做到这一点,因为其速度远低于绳索拉伸的速度. 然而,蚂蚁最终会达到相反的结局.

当蚂蚁甚至还没有开始移动时,它前面有100%的绳索. 过了一秒钟,绳子就变大了,但蚂蚁也走了一定的距离,如果按百分比计算,它必须经过的距离就会减少——它已经不到100%,尽管并不多.

虽然绳索不断拉伸,但蚂蚁行走的小距离也变得更大. 虽然绳索不断拉长,但蚂蚁的路径却每秒都变得略小. 蚂蚁继续以恒定的速度前进. 因此,随着每一秒,他已经旅行的距离增加,必须经过的距离减少. 当然是百分比

问题的解决有一个条件:蚂蚁必须是不朽的. 因此,蚂蚁会在2.8×1043.429秒内到达终点,这比宇宙存在的时间略长.

8. 国家 捕食者-猎物模型是一个描述真实生态状况的方程式. 例如,模型可以确定森林中的狐兔数量会改变多少. 我们假设兔子所吃的草在森林中越来越丰富。 我们可以假设这种结果对兔子有利,因为有了大量的草,它们就会很好地繁殖,增加数量.

生态平衡的悖论认为,情况并非如此:第一,兔子的数量确实会增加,但是兔子在封闭环境中(森林)的人口增长会导致狐狸的人口增长. 之后捕食者的数量会增加很多,以至于首先会摧毁所有的猎物,然后自己死去.

在实践中,这个悖论并不适用于大多数动物物种,如果仅仅是因为它们生活在封闭的环境中,所以动物种群是稳定的. 此外,动物还可以进化:例如,在新的条件下,猎物会拥有新的防御机制.

9. 国家 召集一群朋友一起观看这段视频. 完成后,让每个人发表意见,无论声音在全部四声调中增减. 你会惊讶的 答案会有多不同

要理解这个悖论,你需要了解一些音乐笔记. 每个音符都有一定的高度,取决于我们是否听到高音或低音. 下一个更高的八元音符的音符,音符的音符比上一个八元音符的音符高一倍. 每个八角星可以分为两个等长的三吨间隔.

在视频中,一只纽特将每对声音分开. 在每对音中,一个音是来自不同的八进制音符的相同音符的混合物——例如,一个音符比另一个音符高的前两个音符的组合. 当纽特语中的声音从一个音符传到另一个音符(例如,两个音符之间的单音符)时,将音符解释为高于或低于前一个音符是完全合理的.

另外一个自相矛盾的Newts属性是感觉声音在不断下降,尽管音调没有改变. 在我们的视频中,你可以看到 影响长达10分钟。

10个 在你们之前,两杯水,除了一个,都完全一样: 左边玻璃的水温度比右边高. 把两副眼镜都放在冰箱里 哪个杯子能更快地冻结水? 你可以决定,在右边, 水原本比较冷, 但热水会比水在室温下冷。

这种奇怪的效果以1986年一名坦桑尼亚学生在冷冻牛奶以制造冰激凌时观察到它的名字命名. 一些最伟大的思想家——亚里士多德、弗朗西斯·培根和勒内·笛卡尔——以前曾提到过这一现象,但一直无法解释。 例如,亚里士多德假设,在与质量相反的环境中,质量会提高。

由于若干因素,Mpemba效应是可能的。 一杯热水中的水可能更少,因为部分水会蒸发,因此,水应该更少地结冰. 另外,热水中含有的气体较少,这意味着对流在这种水中会更容易发生,因此更容易将其冻结.

另一种理论认为,把水分子放在一起的化学结合会减弱. 水分子由两个氢原子结合为一个氧原子组成. 当水被加热时,分子会略微移动,它们之间的联结减弱,分子会失去一些能量——这可以使热水比冷水冷却更快.

资料来源:脑暴-blog.ru。

资料来源:/用户/1080。