549
选择不是显而易见的:4矛盾的概率论
"有三种谎言谎言,该死的谎言,统计数据的"。 这句话,因为马克*吐温,英国首相本杰明*迪斯累里,以及反映了态度的大多数数学的法律。 事实上,概率论有时引发令人惊讶的事实,很难相信一见钟情—是谁,尽管如此,已经证实的科学。 "理论和实践"记得的最着名悖论。
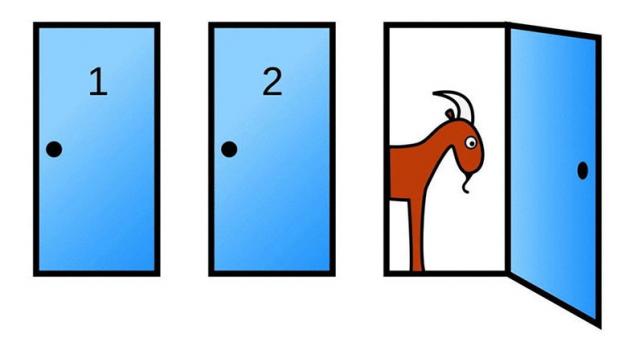
蒙特门的问题是 究竟这个问题在电影"二十一条"建议的狡猾麻省理工学院教授。 给出正确的回答,主角落入组的辉煌的年轻数学家,玩的赌城拉斯维加斯。
经典的制定是:"假定某玩家被邀请参加在美国着名的电视节目让我们做个交易,这导致巨大厅,他必须选择一个三个门。 后面两个门都是山羊,一个是奖,该汽车时,主持人知道的位置奖项。 之后的播放,使得他所选择的,主持人打开一个剩余的大门,后面是一头山羊,并提供了手要改变他的想法。 应该玩家同意或者它是更好保持你的初始选择吗?"
这里是一个典型的推理:在东道已经打开了一扇门,并表明一个山羊的,玩家之间进行选择两门。 汽车的背后是他们中的一个,则该概率的其猜is½的。 因此,没有区别—以改变你的选择或没有。 尽管如此,概率论说,它可能增加获胜的机会通过改变决定。 我们将理解为什么会这样。
这后一步骤。 在那一刻,当我们做了我们最初选择,我们必须分门为两个部分:选择和其他两个。 显而易见的是,该概率是,该车的背后隐藏"我们的"门is⅓,分别该车后面的一两个剩余的门probability⅔的。 当东道显示,后面那些门是一个山羊的,事实证明,⅔的机会,可以在第二门。 和驱动者的选择两门,后面的其中之一(最初选择的)的汽车,是一个概率of⅓,另一个概率of⅔的。 选择变得显而易见的。 当然,这并不否定这一事实,从一开始玩家可以选择的门有汽车。

问题的三个囚徒 的悖论三个囚犯类似于蒙特门的问题,虽然该行动是在更戏剧性的条件。 三名囚犯(A、B和C)被判处死刑并置于单独监禁。 总督随机选择他们,并给了他一个赦免。 典狱长都知道,这三个赦免,但他被告知要保守这个秘密。 囚犯一个问门卫告诉他名称的第二囚禁(除了自己的),谁肯定会被执行的:"如果被赦免,告诉我什么将执行如果得到赦免,告诉我,执行将B.如果他们两个将被执行和赦免我吧,掷硬币,并告诉任何这两个名称。" 典狱长说,囚犯将被执行B.我们应该庆幸的囚犯,对吧?
这似乎是。 在收到该信息之后,死亡的概率的一个囚犯和was⅔,现在他知道之一,其他两名囚犯将被执行,因此概率为他的执行有所减少to½的。 但事实上的囚犯和没有了解到任何新的东西:如果他不是被赦免,他会打电话的另一名囚犯,所以他知道那人剩下的两个将被执行。 如果他很幸运,并执行被取消了,他听到一个随机的名字B或C。因此,他的救赎的机会并没有改变。
现在想象一下,有人剩余的囚犯知道有关囚犯的问题和答案。 它会改变他的看法的概率赦免。
如果谈话中听到囚犯B,他得知他的精确执行的。 如果囚犯,然后概率的赦免将be⅔的。 为什么会发生这种事? 囚犯并没有收到任何信息,他的机会,赦免是still⅓的。 囚犯会肯定不会赦免,他的机会是零。 因此,可能自由会被释放的三名囚犯,是相等的to⅔的。

两个信封悖论 这种矛盾已经成为众所周知由于数学的马丁*加德纳和阐明如下:"假设你和另一个提供两个信封,其中一个是一定数额的金钱X和其他的金额的两倍。 你有彼此独立地打开信封、数钱,然后可以交换他们。 该信封是相同的,因此可能,你将得到的信封用的小量,is½的。 假设你打开信封,发现有10美元。 因此,在信封你的朋友可能是同样可能的5美元或20美元。 如果你决定交换,也是可以计算的数学期望值总额—也就是说,其平均值。 这是1/2倍$5+1/2×20=$12,5. 因此,交流有益于你。 而且,最有可能的,你的朋友会因相同的方式。 但显而易见的是,交换可能不有益于你。 什么是错误的吗?"
矛盾的是,直到你打开了你的信封中,该概率表现良好:你做的有50%的机会找到你的信封量×50%的数额2倍。 和常识告诉我们,有关信息的流量,可以在不影响的内容的第二个信封。
然而,尽快为您打开信封,情况急剧变化(这种自相矛盾的现象是有点类似的故事,薛定谔的猫,那里的存在的一个观察者影响的情况)。 事实上,遵守情况的条款矛盾的概率找到第二个信封或大或小的数额,比你应该相同。 但随后同样可能有任何价值的这笔款项从零到无限的。 但是,如果同样无限多的可能性,他们总是无限的。 但这是不可能的。
为了清楚起见,可以想象一下,你找到你的信封一个%。 显而易见的是,第二个信封不可数额一半。
有趣的是,讨论有关决议的矛盾继续在本。 在同一时间尝试如何解释自相矛盾的内制定的最佳策略,在这种情况。 特别是,教授托马斯*盖提出了一个原始的方法来战略的组成改变或不改变信封,遵循一种直观的期望。 例如,如果你打开信封,并找到一美元的10—一个小数额的估计—这是值得的交换。 如果这信封是,比如说,1 000美元,超过最疯狂的期望,然后变化不是必要的。 这种直观的战略的情况下定期提供选择的两个信封,使得有可能增加的总收益超过该战略不断变化的信封。

矛盾的男孩和女孩 这种自相矛盾的现象是提议由马丁*加德纳和制定为:"史密斯先生有两个孩子。 至少一个孩子一个男孩。 什么样的的概率,二是还有一个男孩吗?"
这似乎说,任务很简单。 但是,如果你开始了解,发现一个奇怪的事实:正确的答案将有所不同,这取决于我们如何计算的概率性的其他儿童。
备选案文1
考虑所有可能的组合家庭中与两个孩子:
—女孩/女孩
—女孩/男孩
—男孩/女孩
—男孩/男孩
选项的女孩/女孩不适合我们这个任务。 因此,对于家族史密斯先生,有三个同样可能的选择,因此,该概率是其他的孩子也是一个男孩,is⅓的。 这个答案是由加德纳开始。
备选案文2
想象一下,我们满足史密斯先生在大街上,当他走他的儿子。 什么样的的概率,第二个孩子—还有一个男孩吗? 由于性别的第二个孩子并不取决于性别,首先,显而易见的(和正确的)的答案is½的。
为什么发生这种情况,因为这似乎是没有什么改变了?
这一切都取决于我们如何处理这一问题的计算概率。 在第一种情况下,我们认为所有可能的变型的史密斯的家庭。 第二,我们认为所有的家庭属于强制性的"必须是一个孩子"。 计算概率性的第二个孩子进行了这种情况(概率论这就是所谓的"有条件的概率"),它导致的结果是不同的。 出版
P.S.记住,仅仅通过改变他们的消费—我们一起改变世界了。 你加入我们在Facebook,脸谱了,语音
资料来源:theoryandpractice.ru/posts/7518-paradoks-probability

蒙特门的问题是 究竟这个问题在电影"二十一条"建议的狡猾麻省理工学院教授。 给出正确的回答,主角落入组的辉煌的年轻数学家,玩的赌城拉斯维加斯。
经典的制定是:"假定某玩家被邀请参加在美国着名的电视节目让我们做个交易,这导致巨大厅,他必须选择一个三个门。 后面两个门都是山羊,一个是奖,该汽车时,主持人知道的位置奖项。 之后的播放,使得他所选择的,主持人打开一个剩余的大门,后面是一头山羊,并提供了手要改变他的想法。 应该玩家同意或者它是更好保持你的初始选择吗?"
这里是一个典型的推理:在东道已经打开了一扇门,并表明一个山羊的,玩家之间进行选择两门。 汽车的背后是他们中的一个,则该概率的其猜is½的。 因此,没有区别—以改变你的选择或没有。 尽管如此,概率论说,它可能增加获胜的机会通过改变决定。 我们将理解为什么会这样。
这后一步骤。 在那一刻,当我们做了我们最初选择,我们必须分门为两个部分:选择和其他两个。 显而易见的是,该概率是,该车的背后隐藏"我们的"门is⅓,分别该车后面的一两个剩余的门probability⅔的。 当东道显示,后面那些门是一个山羊的,事实证明,⅔的机会,可以在第二门。 和驱动者的选择两门,后面的其中之一(最初选择的)的汽车,是一个概率of⅓,另一个概率of⅔的。 选择变得显而易见的。 当然,这并不否定这一事实,从一开始玩家可以选择的门有汽车。

问题的三个囚徒 的悖论三个囚犯类似于蒙特门的问题,虽然该行动是在更戏剧性的条件。 三名囚犯(A、B和C)被判处死刑并置于单独监禁。 总督随机选择他们,并给了他一个赦免。 典狱长都知道,这三个赦免,但他被告知要保守这个秘密。 囚犯一个问门卫告诉他名称的第二囚禁(除了自己的),谁肯定会被执行的:"如果被赦免,告诉我什么将执行如果得到赦免,告诉我,执行将B.如果他们两个将被执行和赦免我吧,掷硬币,并告诉任何这两个名称。" 典狱长说,囚犯将被执行B.我们应该庆幸的囚犯,对吧?
这似乎是。 在收到该信息之后,死亡的概率的一个囚犯和was⅔,现在他知道之一,其他两名囚犯将被执行,因此概率为他的执行有所减少to½的。 但事实上的囚犯和没有了解到任何新的东西:如果他不是被赦免,他会打电话的另一名囚犯,所以他知道那人剩下的两个将被执行。 如果他很幸运,并执行被取消了,他听到一个随机的名字B或C。因此,他的救赎的机会并没有改变。
现在想象一下,有人剩余的囚犯知道有关囚犯的问题和答案。 它会改变他的看法的概率赦免。
如果谈话中听到囚犯B,他得知他的精确执行的。 如果囚犯,然后概率的赦免将be⅔的。 为什么会发生这种事? 囚犯并没有收到任何信息,他的机会,赦免是still⅓的。 囚犯会肯定不会赦免,他的机会是零。 因此,可能自由会被释放的三名囚犯,是相等的to⅔的。

两个信封悖论 这种矛盾已经成为众所周知由于数学的马丁*加德纳和阐明如下:"假设你和另一个提供两个信封,其中一个是一定数额的金钱X和其他的金额的两倍。 你有彼此独立地打开信封、数钱,然后可以交换他们。 该信封是相同的,因此可能,你将得到的信封用的小量,is½的。 假设你打开信封,发现有10美元。 因此,在信封你的朋友可能是同样可能的5美元或20美元。 如果你决定交换,也是可以计算的数学期望值总额—也就是说,其平均值。 这是1/2倍$5+1/2×20=$12,5. 因此,交流有益于你。 而且,最有可能的,你的朋友会因相同的方式。 但显而易见的是,交换可能不有益于你。 什么是错误的吗?"
矛盾的是,直到你打开了你的信封中,该概率表现良好:你做的有50%的机会找到你的信封量×50%的数额2倍。 和常识告诉我们,有关信息的流量,可以在不影响的内容的第二个信封。
然而,尽快为您打开信封,情况急剧变化(这种自相矛盾的现象是有点类似的故事,薛定谔的猫,那里的存在的一个观察者影响的情况)。 事实上,遵守情况的条款矛盾的概率找到第二个信封或大或小的数额,比你应该相同。 但随后同样可能有任何价值的这笔款项从零到无限的。 但是,如果同样无限多的可能性,他们总是无限的。 但这是不可能的。
为了清楚起见,可以想象一下,你找到你的信封一个%。 显而易见的是,第二个信封不可数额一半。
有趣的是,讨论有关决议的矛盾继续在本。 在同一时间尝试如何解释自相矛盾的内制定的最佳策略,在这种情况。 特别是,教授托马斯*盖提出了一个原始的方法来战略的组成改变或不改变信封,遵循一种直观的期望。 例如,如果你打开信封,并找到一美元的10—一个小数额的估计—这是值得的交换。 如果这信封是,比如说,1 000美元,超过最疯狂的期望,然后变化不是必要的。 这种直观的战略的情况下定期提供选择的两个信封,使得有可能增加的总收益超过该战略不断变化的信封。

矛盾的男孩和女孩 这种自相矛盾的现象是提议由马丁*加德纳和制定为:"史密斯先生有两个孩子。 至少一个孩子一个男孩。 什么样的的概率,二是还有一个男孩吗?"
这似乎说,任务很简单。 但是,如果你开始了解,发现一个奇怪的事实:正确的答案将有所不同,这取决于我们如何计算的概率性的其他儿童。
备选案文1
考虑所有可能的组合家庭中与两个孩子:
—女孩/女孩
—女孩/男孩
—男孩/女孩
—男孩/男孩
选项的女孩/女孩不适合我们这个任务。 因此,对于家族史密斯先生,有三个同样可能的选择,因此,该概率是其他的孩子也是一个男孩,is⅓的。 这个答案是由加德纳开始。
备选案文2
想象一下,我们满足史密斯先生在大街上,当他走他的儿子。 什么样的的概率,第二个孩子—还有一个男孩吗? 由于性别的第二个孩子并不取决于性别,首先,显而易见的(和正确的)的答案is½的。
为什么发生这种情况,因为这似乎是没有什么改变了?
这一切都取决于我们如何处理这一问题的计算概率。 在第一种情况下,我们认为所有可能的变型的史密斯的家庭。 第二,我们认为所有的家庭属于强制性的"必须是一个孩子"。 计算概率性的第二个孩子进行了这种情况(概率论这就是所谓的"有条件的概率"),它导致的结果是不同的。 出版
P.S.记住,仅仅通过改变他们的消费—我们一起改变世界了。 你加入我们在Facebook,脸谱了,语音
资料来源:theoryandpractice.ru/posts/7518-paradoks-probability