550
Вибір не очевидний: 4 парадокси теорії ймовірності
Є три види брехні: кришка, кришка і статистика. Ця фраза, приписана Марком Твеном до Британського прем’єр-міністра Benjamin Disraeli, відображає ставлення більшості до математичних законів. Дійсно, теорія ймовірності іноді кидає дивовижних фактів, які важко вірити на першому погляді, і що жодним чином не підтримується наукою. Історії та практики згадували найвідоміші парадокси.
 р.
р.
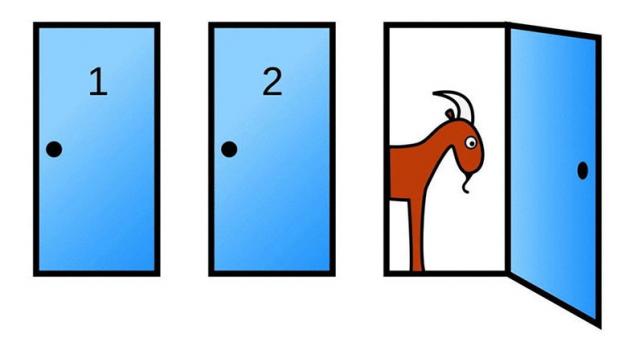
Проблема Монті Холл Це завдання у фільмі «Твенті-Од» пропонувала студентам кінні МІТ професора. Відповідаючи праву відповідь, головний герой отримує в команду блискучих молодих математиків, які збивають казино в Лас-Вегасі.
Давайте скажемо певний програвач для участі в знаменитому американський телевізійному шоу Let's Make Deal, який знаходиться в Монті Холл, і він повинен вибрати один з трьох дверей. За двома дверима є кози, за одну - головна премія, автомобіль, господар знає розташування призів. Після того, як гравець робить свій вибір, ведучий відкриває одну з решти дверей, за якою знаходиться коза, і запрошує гравців змінити своє рішення. Якщо гравець погоджується або повинен зберігати свій оригінальний вибір?
Ось типова лінія причин: після того, як ведучий відкрив один з дверей і продемонстрував коза, гравець залишається вибрати між двома дверима. Машина за одну з них, тому ймовірність вгадати її 1⁄2. Ви не знаєте, чи змінити свій вибір або ні. Тим не менш, теорія ймовірності вказує, що ви можете збільшити ваші шанси на виграш, змінивши Ваше рішення. Давайте подивимося, чому це.
Так нехай крок назад. На даний момент ми зробили наш початковий вибір, ми розбиваємо двері на дві частини: один ми обрали і другий. Очевидно, що автомобіль ховається за дверима «ур» становить 1⁄3 – відповідно, автомобіль стоїть за одним з двох залишилися дверей з ймовірністю 2⁄3. Коли ведучий показує, що за одним з цих дверей є козак, виходить, що ці дві третини шансів падають на другий двері. І це зменшує вибір гравця до двох дверей, за одним з яких (оригінально підібраний) автомобіль з ймовірністю 1⁄3, а за іншим - з ймовірністю 2⁄3. Вибір стає очевидним. Це, звичайно, не змінює факт, що з самого початку гравець може вибрати двері з автомобілем.

Завдання трьох в'язнів Парадокс трьох в'язнів схожий на це Монті Холл, хоча дія відбувається в більш драматичних налаштуваннях. Три в'язниці (А, Б і Б) були засуджені до смерті і розміщені в одиночній конфінації. Намісник випадково обирає один з них і надає йому пародонту. Війна знає, що з трьох було припарковано, але він зобов'язаний тримати його секретом. В'язниця Попитає охорону, щоб розповісти йому ім'я другого в'язниці (як і сам), які обов'язково будуть виконані: Якщо B pardoned, розкажіть, що B буде виконано. Якщо вони обидва виконані, і я приймав, щоб монети і сказати або з цих двох назв. Warden коментує в'язниця B буде виконана. Чи варто в'язувати родзинку?
Ви думаєте так. Після цього, перед отриманням цієї інформації, ймовірність смерті ув'язненого А було 2⁄3, і тепер він знає, що один з інших двох ув'язнених буде виконаний - тому ймовірність його виконання знизився до 1⁄2. Але насправді в'язниця А нічого не дізнався: якщо він не був запалений, він буде дано ім'я іншої в'язниці, і він вже знав, що один з двох залишилися в'язниці буде виконаний. Якщо він щасливий, і виконання скасовано, він почне випадкове ім'я B або B. Його шанси на виживання не змінилися.
Тепер уявіть, що один з решти тюрмортів дізнається про це питання та відповідь в'язниці. Це змінить своє сприйняття подібності пародонту.
Якщо в'язниця Він знає, що він буде виконуватися. І якщо в'язниця Б, то ймовірність його пародонту буде 2⁄3. Чому це сталося? В'язниця Не отримав ніякої інформації, а його шанси на пародонту ще 1⁄3. В'язниця B обов'язково не буде пародондом, і його шанси є нульовими. Імовірність, що третій ув'язнений буде випущений 2⁄3.

Парадокс двох конвертів Цей парадокс був відомий завдяки математику Мартін Гарднеру, і розроблений таким чином: Вам і другу були запропоновані два конверти, одна з яких містить певну кількість грошей X, а інший - двічі на суму. Ви самостійно відкриваєте конверти, відрахуйте гроші, а потім можете обмінювати їх. Конверти однакові, тому ймовірність, що ви отримаєте конверт з меншою кількістю 1⁄2. Припустимо, ви відкриваєте конверт і знайдіть $10 в ньому. Таким чином, конверт вашого друга може бути якомога швидше за $ 5 або $ 20. Якщо ви вирішили обміняти, то можна розрахувати математичне очікування загальної суми - тобто його середня вартість. 1/2кс$5+1/2×20=$12,5. Так, обмін буде добре для вас. Ваш друг, ймовірно, подумати те саме. Але, очевидно, обмін не може бути вигідним для вас. Що таке помилка?
Парадокс є те, що до тих пір, поки ви відкриєте конверт, ймовірності будуть досить добре: ви дійсно маєте 50 відсотків шанс знайти суму X в конверті і 50 відсотків шанс знайти суму 2X в конверті. І поширене почуття диктує, що інформація про суму, яку ви не можете вплинути на вміст другого конверту.
Однак, як тільки ви відкриваєте конверт, ситуація кардинально змінюється (це парадокс дещо схожий на історію кота Шредінгера, де дуже присутність спостерігача впливає на стан справ). Справа в тому, що для того, щоб відповідати умовам парадоксу, ймовірність знаходження в другому конверті більша або менша кількість, ніж ви повинні бути однаковими. Але потім будь-яке значення цієї суми від нуля до нескінченності однаково допустиме. І якщо нескінченна кількість можливостей однаково допустима, вони додають до нескінченності. Це неможливо.
Для чіткості можна уявити, що ви знайдете один цент у конверті. Очевидно, що другий конверт не може містити половину суми.
Цікаво, що дискусії про вирішення парадоксу продовжуються сьогодні. У той же час, спроби, як роз’яснити парадокс з внутрішньої сторони і розробити найкращу стратегію поведінки в такій ситуації. Зокрема, професор Томас Cover запропонував оригінальний підхід до формування стратегії - змінити або не змінювати конверт, направляючись деякими інтуїтивно зрозумілими очікуваннями. Наприклад, якщо ви відкриваєте конверт і знаходите $10 в ньому – невелика кількість за вашими оцінками – вам слід обміняти його. І якщо конверт, скажеш, $1,000, який перевищує ваші найдикіші очікування, то не змінить. Ця інтуїтивно зрозуміла стратегія, якщо ви регулярно попросите вибрати два конверти, дає вам можливість збільшити загальну перемогу більше, ніж стратегія постійно мінливих конвертів.

Парадокс хлопчика та дівчини Цей парадокс також був запропонований Мартіном Гарднером і розроблений таким чином: Пан Сміт є двома дітьми. Не менше однієї дитини хлопчик. Яка ймовірність того, що інший ще хлопчик?
Здавалося б, що завдання просто. Однак, якщо ми починаємо розуміти, ми знайдемо цікавий обхват: правильну відповідь буде відрізнятися в залежності від того, як ми розраховуємо ймовірність сексу іншої дитини.
Варіант 1
Розглянемо всі можливі комбінації в сім'ях з двома дітьми:
- Дівчина/Дівчина
- Дівчина/Бой
- Хлопчик / Дівчинка
- Хлопчик/Бой
Дівчина/дівчина варіант не підходить для нас. Так є три однаково ймовірні варіанти сім'ї Сміта - що означає, що ймовірність, що ще одна дитина також буде хлопчиком 1⁄3. Це відповідь Гарднер спочатку дав.
Варіант 2
Ми познайомимося з паном Смітом на вулиці, поки він з сина. Яка ймовірність, що друга дитина також хлопчик? Так як секс другої дитини не залежить від сексу першого, явний (і правильно) відповідь 1⁄2.
Чому це відбувається, коли нічого не хоче змінити?
Все залежить від того, як ми підходимо до питання ймовірності. У першому випадку ми розглянемо всі можливі варіанти сімейства Сміт. У другому випадку ми подивимося на всіх сім'ях, які підлягають обов'язковому умові «повний бути одним хлопчиком». Розрахунок ймовірності сексу другої дитини проведено з такою умовою (в теорії ймовірності це називається «звичайна ймовірність»), яка призвела до результату, відрізняється від першого.
P.S. І пам'ятайте, що просто змінивши наше споживання, ми змінюємо світ разом! Приєднуйтесь до нас на Facebook, VKontakte, Odnoklassniki
Джерело: теоріяandpractice.ru/posts/7518-paradoks-probability
 р.
р.Проблема Монті Холл Це завдання у фільмі «Твенті-Од» пропонувала студентам кінні МІТ професора. Відповідаючи праву відповідь, головний герой отримує в команду блискучих молодих математиків, які збивають казино в Лас-Вегасі.
Давайте скажемо певний програвач для участі в знаменитому американський телевізійному шоу Let's Make Deal, який знаходиться в Монті Холл, і він повинен вибрати один з трьох дверей. За двома дверима є кози, за одну - головна премія, автомобіль, господар знає розташування призів. Після того, як гравець робить свій вибір, ведучий відкриває одну з решти дверей, за якою знаходиться коза, і запрошує гравців змінити своє рішення. Якщо гравець погоджується або повинен зберігати свій оригінальний вибір?
Ось типова лінія причин: після того, як ведучий відкрив один з дверей і продемонстрував коза, гравець залишається вибрати між двома дверима. Машина за одну з них, тому ймовірність вгадати її 1⁄2. Ви не знаєте, чи змінити свій вибір або ні. Тим не менш, теорія ймовірності вказує, що ви можете збільшити ваші шанси на виграш, змінивши Ваше рішення. Давайте подивимося, чому це.
Так нехай крок назад. На даний момент ми зробили наш початковий вибір, ми розбиваємо двері на дві частини: один ми обрали і другий. Очевидно, що автомобіль ховається за дверима «ур» становить 1⁄3 – відповідно, автомобіль стоїть за одним з двох залишилися дверей з ймовірністю 2⁄3. Коли ведучий показує, що за одним з цих дверей є козак, виходить, що ці дві третини шансів падають на другий двері. І це зменшує вибір гравця до двох дверей, за одним з яких (оригінально підібраний) автомобіль з ймовірністю 1⁄3, а за іншим - з ймовірністю 2⁄3. Вибір стає очевидним. Це, звичайно, не змінює факт, що з самого початку гравець може вибрати двері з автомобілем.

Завдання трьох в'язнів Парадокс трьох в'язнів схожий на це Монті Холл, хоча дія відбувається в більш драматичних налаштуваннях. Три в'язниці (А, Б і Б) були засуджені до смерті і розміщені в одиночній конфінації. Намісник випадково обирає один з них і надає йому пародонту. Війна знає, що з трьох було припарковано, але він зобов'язаний тримати його секретом. В'язниця Попитає охорону, щоб розповісти йому ім'я другого в'язниці (як і сам), які обов'язково будуть виконані: Якщо B pardoned, розкажіть, що B буде виконано. Якщо вони обидва виконані, і я приймав, щоб монети і сказати або з цих двох назв. Warden коментує в'язниця B буде виконана. Чи варто в'язувати родзинку?
Ви думаєте так. Після цього, перед отриманням цієї інформації, ймовірність смерті ув'язненого А було 2⁄3, і тепер він знає, що один з інших двох ув'язнених буде виконаний - тому ймовірність його виконання знизився до 1⁄2. Але насправді в'язниця А нічого не дізнався: якщо він не був запалений, він буде дано ім'я іншої в'язниці, і він вже знав, що один з двох залишилися в'язниці буде виконаний. Якщо він щасливий, і виконання скасовано, він почне випадкове ім'я B або B. Його шанси на виживання не змінилися.
Тепер уявіть, що один з решти тюрмортів дізнається про це питання та відповідь в'язниці. Це змінить своє сприйняття подібності пародонту.
Якщо в'язниця Він знає, що він буде виконуватися. І якщо в'язниця Б, то ймовірність його пародонту буде 2⁄3. Чому це сталося? В'язниця Не отримав ніякої інформації, а його шанси на пародонту ще 1⁄3. В'язниця B обов'язково не буде пародондом, і його шанси є нульовими. Імовірність, що третій ув'язнений буде випущений 2⁄3.

Парадокс двох конвертів Цей парадокс був відомий завдяки математику Мартін Гарднеру, і розроблений таким чином: Вам і другу були запропоновані два конверти, одна з яких містить певну кількість грошей X, а інший - двічі на суму. Ви самостійно відкриваєте конверти, відрахуйте гроші, а потім можете обмінювати їх. Конверти однакові, тому ймовірність, що ви отримаєте конверт з меншою кількістю 1⁄2. Припустимо, ви відкриваєте конверт і знайдіть $10 в ньому. Таким чином, конверт вашого друга може бути якомога швидше за $ 5 або $ 20. Якщо ви вирішили обміняти, то можна розрахувати математичне очікування загальної суми - тобто його середня вартість. 1/2кс$5+1/2×20=$12,5. Так, обмін буде добре для вас. Ваш друг, ймовірно, подумати те саме. Але, очевидно, обмін не може бути вигідним для вас. Що таке помилка?
Парадокс є те, що до тих пір, поки ви відкриєте конверт, ймовірності будуть досить добре: ви дійсно маєте 50 відсотків шанс знайти суму X в конверті і 50 відсотків шанс знайти суму 2X в конверті. І поширене почуття диктує, що інформація про суму, яку ви не можете вплинути на вміст другого конверту.
Однак, як тільки ви відкриваєте конверт, ситуація кардинально змінюється (це парадокс дещо схожий на історію кота Шредінгера, де дуже присутність спостерігача впливає на стан справ). Справа в тому, що для того, щоб відповідати умовам парадоксу, ймовірність знаходження в другому конверті більша або менша кількість, ніж ви повинні бути однаковими. Але потім будь-яке значення цієї суми від нуля до нескінченності однаково допустиме. І якщо нескінченна кількість можливостей однаково допустима, вони додають до нескінченності. Це неможливо.
Для чіткості можна уявити, що ви знайдете один цент у конверті. Очевидно, що другий конверт не може містити половину суми.
Цікаво, що дискусії про вирішення парадоксу продовжуються сьогодні. У той же час, спроби, як роз’яснити парадокс з внутрішньої сторони і розробити найкращу стратегію поведінки в такій ситуації. Зокрема, професор Томас Cover запропонував оригінальний підхід до формування стратегії - змінити або не змінювати конверт, направляючись деякими інтуїтивно зрозумілими очікуваннями. Наприклад, якщо ви відкриваєте конверт і знаходите $10 в ньому – невелика кількість за вашими оцінками – вам слід обміняти його. І якщо конверт, скажеш, $1,000, який перевищує ваші найдикіші очікування, то не змінить. Ця інтуїтивно зрозуміла стратегія, якщо ви регулярно попросите вибрати два конверти, дає вам можливість збільшити загальну перемогу більше, ніж стратегія постійно мінливих конвертів.

Парадокс хлопчика та дівчини Цей парадокс також був запропонований Мартіном Гарднером і розроблений таким чином: Пан Сміт є двома дітьми. Не менше однієї дитини хлопчик. Яка ймовірність того, що інший ще хлопчик?
Здавалося б, що завдання просто. Однак, якщо ми починаємо розуміти, ми знайдемо цікавий обхват: правильну відповідь буде відрізнятися в залежності від того, як ми розраховуємо ймовірність сексу іншої дитини.
Варіант 1
Розглянемо всі можливі комбінації в сім'ях з двома дітьми:
- Дівчина/Дівчина
- Дівчина/Бой
- Хлопчик / Дівчинка
- Хлопчик/Бой
Дівчина/дівчина варіант не підходить для нас. Так є три однаково ймовірні варіанти сім'ї Сміта - що означає, що ймовірність, що ще одна дитина також буде хлопчиком 1⁄3. Це відповідь Гарднер спочатку дав.
Варіант 2
Ми познайомимося з паном Смітом на вулиці, поки він з сина. Яка ймовірність, що друга дитина також хлопчик? Так як секс другої дитини не залежить від сексу першого, явний (і правильно) відповідь 1⁄2.
Чому це відбувається, коли нічого не хоче змінити?
Все залежить від того, як ми підходимо до питання ймовірності. У першому випадку ми розглянемо всі можливі варіанти сімейства Сміт. У другому випадку ми подивимося на всіх сім'ях, які підлягають обов'язковому умові «повний бути одним хлопчиком». Розрахунок ймовірності сексу другої дитини проведено з такою умовою (в теорії ймовірності це називається «звичайна ймовірність»), яка призвела до результату, відрізняється від першого.
P.S. І пам'ятайте, що просто змінивши наше споживання, ми змінюємо світ разом! Приєднуйтесь до нас на Facebook, VKontakte, Odnoklassniki
Джерело: теоріяandpractice.ru/posts/7518-paradoks-probability