550
La elección de la que no son evidentes: 4 la paradoja de la teoría de la probabilidad
"Hay tres tipos de mentiras: la mentira, una mentira y las estadísticas". Esta frase, asignada por mark Твеном primer ministro británico benjamin disraeli, bien refleja la actitud de la mayoría de la matemática la pauta. De hecho, la teoría de las probabilidades a veces echa hechos asombrosos, que es difícil de creer a primera vista — y que, sin embargo, confirmado por la ciencia. "La teoría y la práctica" se acordaron de las más famosas paradojas.
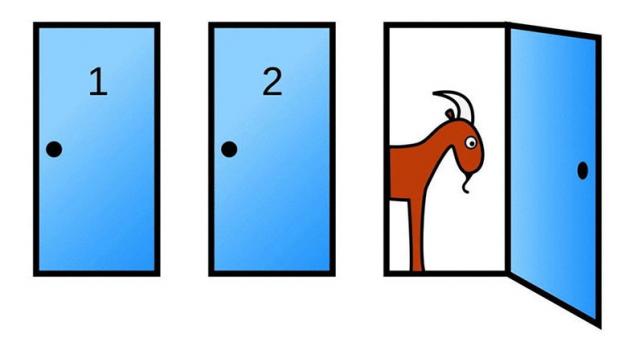
El problema de monty Hall Precisamente de esta tarea en la película "Veinte y uno" invitó a los estudiantes astuto profesor del MIT. Dar la respuesta correcta, el personaje principal se encuentra en el comando de brillantes jóvenes matemáticos, обыгрывающих un casino en las vegas.
El clásico enunciado dice así: "Supongamos que un jugador han invitado a participar en el famoso programa de televisión americano Let's Make a Deal, que conduce de monty Hall, y él tiene que elegir una de las tres puertas. Por dos puertas se encuentran las cabras, por un premio, el coche, el líder conoce la ubicación de los premios. Después de que el jugador hace su elección, el presentador abre una de las restantes puertas, detrás de la cual hay una cabra, y le ofrece la oportunidad de cambiar su decisión. Vale la pena si el jugador de estar de acuerdo o es mejor guardar su selección inicial?"
Éste es un típico razonamiento: después de que el presentador ha abierto una de las puertas y mostró la cabra, el jugador queda elegir entre las dos puertas. La máquina está detrás de uno de ellos, entonces, la probabilidad de acertar es de½. Así que no hay diferencia — para cambiar su selección o no. Y no obstante, la teoría de la probabilidad dice que puede aumentar sus posibilidades de ganar, cambiando la solución. Vamos a ver, ¿por qué esto es así.
Para ello, volvemos a dar un paso atrás. En ese momento, cuando hemos hecho el original de la selección, hemos dividido las puertas en dos partes: la parte seleccionada de nosotros y de los otros dos. Es evidente que la probabilidad de que el coche se esconde detrás de "nuestra" puerta es de ⅓ — en consecuencia, el vehículo se encuentra detrás de una de las dos puertas con una probabilidad de dos tercios. Cuando el presentador muestra que detrás de una de estas puertas — la cabra, resulta que estas dos tercios de oportunidad se producen en la segunda puerta. Y esto reduce la elección del jugador a dos puertas, una de las cuales (originalmente seleccionada) el vehículo se encuentra con una probabilidad de⅓, y por el otro con una probabilidad de dos tercios. La selección se hace evidente. Que, por supuesto, no niega el hecho de que desde el principio el jugador puede elegir la puerta con el coche.

La tarea de los tres presos de la Paradoja de los tres prisioneros similar, con el problema de monty Hall, aunque la acción se desarrolla en las más dramáticas circunstancias. Tres detenidos (A, B y c) condenados a la pena de muerte y colocados en celdas de aislamiento. El gobernador elige aleatoriamente uno de ellos y le da el indulto. Vigilante sabe quién de los tres es perdonada, pero le mandó a guardar el secreto. El preso A pide a los guardianes de decirle el nombre de la segunda de un preso (además de él mismo), que precisa de ser ejecutado: "si B es perdonada, dime que será ejecutado S. Si la misericordia, dime que será ejecutado Si van a ser ejecutados, y fui recibido a misericordia, yo, подбрось moneda, y di a cualquiera de estos dos nombres". Vigilante dice que será ejecutado el preso b. ¿Vale la pena alegrarse encarcelado Y?
Aparentemente, sí. De hecho, hasta la obtención de esta información la probabilidad de la muerte del preso Y era de dos tercios, y ahora se sabe que uno de los otros dos presos de ser ejecutado — entonces, la probabilidad de muerte se redujo a½. Pero, en realidad, el preso Y no se enteró de nada nuevo: si la misericordia no es él, le llamarán el nombre de otro preso, y él ya sabía que alguien de los dos restantes son ejecutados. Si tiene suerte, y han abolido la pena de muerte, se oye un nombre aleatorio B o S. Por lo tanto, sus posibilidades de salvación no han cambiado.
Y ahora imaginemos que alguien de los prisioneros aprende acerca de la cuestión del preso A y la respuesta recibida. Esto cambiará su concepto de probabilidad condicional.
Si la conversación escuche el prisionero B, se entera de que su precisión son ejecutados. Y si el preso, la probabilidad de su indulto será de dos tercios. Por qué se ha producido? El preso no ha recibido ninguna información, y sus posibilidades de indulto sigue⅓. El prisionero B exactamente no será perdonada, y sus posibilidades son nulas. Entonces, la probabilidad de que en la libertad saldrá el tercer prisionero, que es igual a dos tercios.

La paradoja de los dos sobres Esta paradoja se hizo famoso gracias a las matemáticas de martin gardner, y se formula de la siguiente manera: "por ejemplo, Supongamos que sí ofrecieron dos sobres, uno de los cuales est cierta suma de dinero X, y en el otro, se suma a la mitad. Usted independientemente вскрываете sobres, пересчитываете dinero, después de lo cual se puede compartir. Sobres los mismos, por lo tanto, la probabilidad de que usted toma el sobre con una cantidad menor, es de½. Por ejemplo, supongamos que abrió el sobre y encontró en él $10. Por lo tanto, en el sobre de tu amigo puede ser равновероятно $5 o $20. Si usted решаетесь en cambio, es posible calcular la expectativa del total — es decir, su valor promedio. Que es de 1/2x$5+1/2×20=$12,5. Por lo tanto, el cambio le beneficiaría. Y, es muy probable que tu amigo va a razonar de la misma manera. Pero es evidente que el cambio no puede ser beneficioso para ambos. En cuanto el mismo error?"
La paradoja es que hasta que no pusieron de su sobre, la probabilidad de que se comportan actúen con integridad: realmente tienes 50% de posibilidades de detectar en su sobre de la suma de X y un 50 por ciento de la cantidad de 2X. Y el sentido común sugiere que la información sobre su monto no puede influir en el contenido de un segundo sobre.
Sin embargo, tan pronto como usted вскрываете sobre la situación cambia radicalmente (la paradoja es algo similar a la historia con el gato de schrödinger, donde la sola presencia de un observador influye en la situación). El hecho de que para el cumplimiento de las condiciones de la paradoja de la probabilidad de encontrar en el segundo sobre la mayor o menor cantidad de lo que tienes, debe ser el mismo. Pero entonces равновероятно cualquier valor de esta suma de cero a infinito. Y si равновероятно infinito número de posibilidades, en la suma que se dan el infinito. Y esto es imposible.
Para mayor claridad se puede imaginar que usted encuentra en su sobre de un centavo. Es evidente que en el segundo el sobre no puede ser la suma de la mitad.
Es curioso que el debate sobre la resolución de la paradoja continúa en la actualidad. En un intento por explicar la paradoja de dentro y desarrollar la mejor estrategia de la conducta en una situación similar. En particular, el profesor thomas propuso un Cover original enfoque de la formación de la estrategia es cambiar o no cambiar el sobre, guiada por cierto intuitivo a la expectativa. Por ejemplo, si usted abrió el sobre y encontró en él $10 — una pequeña cantidad de su прикидкам — vale la pena cambiar. Y si en el sobre, digamos, $1 000, que supera sus expectativas, cambiar no es necesario. Este sistema intuitivo de la estrategia en caso de que regularmente ofrecen elegir dos sobres, da la oportunidad de aumentar las ganancias más que una estrategia de cambio constante de los sobres.

La paradoja de el niño y la niña Esta paradoja también se propuso martin gardner y se formula así: "El señor smith y dos hijos. Al menos un niño — niño. ¿Cuál es la probabilidad de que el segundo también, muchacho?"
Aparentemente, la tarea es fácil. Sin embargo, si comenzar a explorar, se encuentra una curiosa circunstancia: la respuesta correcta será diferente dependiendo de cómo vamos a calcular la probabilidad de un sexo a otro niño.
Opción 1
Considere todas las combinaciones posibles en las familias con dos hijos:
— La Chica/Chica
— Chica/Chico
— El Niño/La Niña
— El Muchacho/Muchacho
La opción de una niña/chica no es para nosotros de las condiciones de la tarea. Por lo tanto, para la familia del señor smith, son posibles tres равновероятных de la opción, y por lo tanto, la probabilidad de que el otro niño, también resulta ser un niño de verdad, es de⅓. La respuesta y la daba el propio gardner inicialmente.
Opción 2
Supongamos que nos encontramos con el señor smith en la calle, cuando se pasea con su hijo. ¿Cuál es la probabilidad de que un segundo hijo — también el muchacho? Ya que el sexo de su segundo hijo no depende del sexo de la primera, evidente (y correcta) la respuesta es½.
Por qué sucede esto, ya que, aparentemente, no ha cambiado nada?
Todo depende de cómo nos planteamos el tema de calcular probabilidades. En el primer caso, hemos considerado todas las opciones posibles de la familia smith. En la segunda, hemos considerado todos los de la familia, caen bajo el imperativo "debe ser un niño". El cálculo de la probabilidad de sexo de su segundo hijo siga con esta condición (en la teoría de probabilidades, esto se conoce como "la probabilidad condicional"), que llevó a un resultado distinto al de la primera. publicado
P. S. Y recuerde, sólo cambiando su consumo — estamos juntos cambiando el mundo! © Únase a nosotros en Facebook , Twitter, Myspace
Fuente: theoryandpractice.ru/posts/7518-paradoks-probability

El problema de monty Hall Precisamente de esta tarea en la película "Veinte y uno" invitó a los estudiantes astuto profesor del MIT. Dar la respuesta correcta, el personaje principal se encuentra en el comando de brillantes jóvenes matemáticos, обыгрывающих un casino en las vegas.
El clásico enunciado dice así: "Supongamos que un jugador han invitado a participar en el famoso programa de televisión americano Let's Make a Deal, que conduce de monty Hall, y él tiene que elegir una de las tres puertas. Por dos puertas se encuentran las cabras, por un premio, el coche, el líder conoce la ubicación de los premios. Después de que el jugador hace su elección, el presentador abre una de las restantes puertas, detrás de la cual hay una cabra, y le ofrece la oportunidad de cambiar su decisión. Vale la pena si el jugador de estar de acuerdo o es mejor guardar su selección inicial?"
Éste es un típico razonamiento: después de que el presentador ha abierto una de las puertas y mostró la cabra, el jugador queda elegir entre las dos puertas. La máquina está detrás de uno de ellos, entonces, la probabilidad de acertar es de½. Así que no hay diferencia — para cambiar su selección o no. Y no obstante, la teoría de la probabilidad dice que puede aumentar sus posibilidades de ganar, cambiando la solución. Vamos a ver, ¿por qué esto es así.
Para ello, volvemos a dar un paso atrás. En ese momento, cuando hemos hecho el original de la selección, hemos dividido las puertas en dos partes: la parte seleccionada de nosotros y de los otros dos. Es evidente que la probabilidad de que el coche se esconde detrás de "nuestra" puerta es de ⅓ — en consecuencia, el vehículo se encuentra detrás de una de las dos puertas con una probabilidad de dos tercios. Cuando el presentador muestra que detrás de una de estas puertas — la cabra, resulta que estas dos tercios de oportunidad se producen en la segunda puerta. Y esto reduce la elección del jugador a dos puertas, una de las cuales (originalmente seleccionada) el vehículo se encuentra con una probabilidad de⅓, y por el otro con una probabilidad de dos tercios. La selección se hace evidente. Que, por supuesto, no niega el hecho de que desde el principio el jugador puede elegir la puerta con el coche.

La tarea de los tres presos de la Paradoja de los tres prisioneros similar, con el problema de monty Hall, aunque la acción se desarrolla en las más dramáticas circunstancias. Tres detenidos (A, B y c) condenados a la pena de muerte y colocados en celdas de aislamiento. El gobernador elige aleatoriamente uno de ellos y le da el indulto. Vigilante sabe quién de los tres es perdonada, pero le mandó a guardar el secreto. El preso A pide a los guardianes de decirle el nombre de la segunda de un preso (además de él mismo), que precisa de ser ejecutado: "si B es perdonada, dime que será ejecutado S. Si la misericordia, dime que será ejecutado Si van a ser ejecutados, y fui recibido a misericordia, yo, подбрось moneda, y di a cualquiera de estos dos nombres". Vigilante dice que será ejecutado el preso b. ¿Vale la pena alegrarse encarcelado Y?
Aparentemente, sí. De hecho, hasta la obtención de esta información la probabilidad de la muerte del preso Y era de dos tercios, y ahora se sabe que uno de los otros dos presos de ser ejecutado — entonces, la probabilidad de muerte se redujo a½. Pero, en realidad, el preso Y no se enteró de nada nuevo: si la misericordia no es él, le llamarán el nombre de otro preso, y él ya sabía que alguien de los dos restantes son ejecutados. Si tiene suerte, y han abolido la pena de muerte, se oye un nombre aleatorio B o S. Por lo tanto, sus posibilidades de salvación no han cambiado.
Y ahora imaginemos que alguien de los prisioneros aprende acerca de la cuestión del preso A y la respuesta recibida. Esto cambiará su concepto de probabilidad condicional.
Si la conversación escuche el prisionero B, se entera de que su precisión son ejecutados. Y si el preso, la probabilidad de su indulto será de dos tercios. Por qué se ha producido? El preso no ha recibido ninguna información, y sus posibilidades de indulto sigue⅓. El prisionero B exactamente no será perdonada, y sus posibilidades son nulas. Entonces, la probabilidad de que en la libertad saldrá el tercer prisionero, que es igual a dos tercios.

La paradoja de los dos sobres Esta paradoja se hizo famoso gracias a las matemáticas de martin gardner, y se formula de la siguiente manera: "por ejemplo, Supongamos que sí ofrecieron dos sobres, uno de los cuales est cierta suma de dinero X, y en el otro, se suma a la mitad. Usted independientemente вскрываете sobres, пересчитываете dinero, después de lo cual se puede compartir. Sobres los mismos, por lo tanto, la probabilidad de que usted toma el sobre con una cantidad menor, es de½. Por ejemplo, supongamos que abrió el sobre y encontró en él $10. Por lo tanto, en el sobre de tu amigo puede ser равновероятно $5 o $20. Si usted решаетесь en cambio, es posible calcular la expectativa del total — es decir, su valor promedio. Que es de 1/2x$5+1/2×20=$12,5. Por lo tanto, el cambio le beneficiaría. Y, es muy probable que tu amigo va a razonar de la misma manera. Pero es evidente que el cambio no puede ser beneficioso para ambos. En cuanto el mismo error?"
La paradoja es que hasta que no pusieron de su sobre, la probabilidad de que se comportan actúen con integridad: realmente tienes 50% de posibilidades de detectar en su sobre de la suma de X y un 50 por ciento de la cantidad de 2X. Y el sentido común sugiere que la información sobre su monto no puede influir en el contenido de un segundo sobre.
Sin embargo, tan pronto como usted вскрываете sobre la situación cambia radicalmente (la paradoja es algo similar a la historia con el gato de schrödinger, donde la sola presencia de un observador influye en la situación). El hecho de que para el cumplimiento de las condiciones de la paradoja de la probabilidad de encontrar en el segundo sobre la mayor o menor cantidad de lo que tienes, debe ser el mismo. Pero entonces равновероятно cualquier valor de esta suma de cero a infinito. Y si равновероятно infinito número de posibilidades, en la suma que se dan el infinito. Y esto es imposible.
Para mayor claridad se puede imaginar que usted encuentra en su sobre de un centavo. Es evidente que en el segundo el sobre no puede ser la suma de la mitad.
Es curioso que el debate sobre la resolución de la paradoja continúa en la actualidad. En un intento por explicar la paradoja de dentro y desarrollar la mejor estrategia de la conducta en una situación similar. En particular, el profesor thomas propuso un Cover original enfoque de la formación de la estrategia es cambiar o no cambiar el sobre, guiada por cierto intuitivo a la expectativa. Por ejemplo, si usted abrió el sobre y encontró en él $10 — una pequeña cantidad de su прикидкам — vale la pena cambiar. Y si en el sobre, digamos, $1 000, que supera sus expectativas, cambiar no es necesario. Este sistema intuitivo de la estrategia en caso de que regularmente ofrecen elegir dos sobres, da la oportunidad de aumentar las ganancias más que una estrategia de cambio constante de los sobres.

La paradoja de el niño y la niña Esta paradoja también se propuso martin gardner y se formula así: "El señor smith y dos hijos. Al menos un niño — niño. ¿Cuál es la probabilidad de que el segundo también, muchacho?"
Aparentemente, la tarea es fácil. Sin embargo, si comenzar a explorar, se encuentra una curiosa circunstancia: la respuesta correcta será diferente dependiendo de cómo vamos a calcular la probabilidad de un sexo a otro niño.
Opción 1
Considere todas las combinaciones posibles en las familias con dos hijos:
— La Chica/Chica
— Chica/Chico
— El Niño/La Niña
— El Muchacho/Muchacho
La opción de una niña/chica no es para nosotros de las condiciones de la tarea. Por lo tanto, para la familia del señor smith, son posibles tres равновероятных de la opción, y por lo tanto, la probabilidad de que el otro niño, también resulta ser un niño de verdad, es de⅓. La respuesta y la daba el propio gardner inicialmente.
Opción 2
Supongamos que nos encontramos con el señor smith en la calle, cuando se pasea con su hijo. ¿Cuál es la probabilidad de que un segundo hijo — también el muchacho? Ya que el sexo de su segundo hijo no depende del sexo de la primera, evidente (y correcta) la respuesta es½.
Por qué sucede esto, ya que, aparentemente, no ha cambiado nada?
Todo depende de cómo nos planteamos el tema de calcular probabilidades. En el primer caso, hemos considerado todas las opciones posibles de la familia smith. En la segunda, hemos considerado todos los de la familia, caen bajo el imperativo "debe ser un niño". El cálculo de la probabilidad de sexo de su segundo hijo siga con esta condición (en la teoría de probabilidades, esto se conoce como "la probabilidad condicional"), que llevó a un resultado distinto al de la primera. publicado
P. S. Y recuerde, sólo cambiando su consumo — estamos juntos cambiando el mundo! © Únase a nosotros en Facebook , Twitter, Myspace
Fuente: theoryandpractice.ru/posts/7518-paradoks-probability