546
The choice is not obvious: 4 the paradox of probability theory
"There are three kinds of lies: lies, damned lies, and statistics". This phrase, attributed to mark TWAIN, Prime Minister of great Britain Benjamin Disraeli, well reflects the attitude of the majority to mathematical laws. Indeed, probability theory sometimes throws surprising facts that are hard to believe at first sight — and who, nevertheless, been confirmed by science. "Theory and practice" remember the most famous paradoxes.
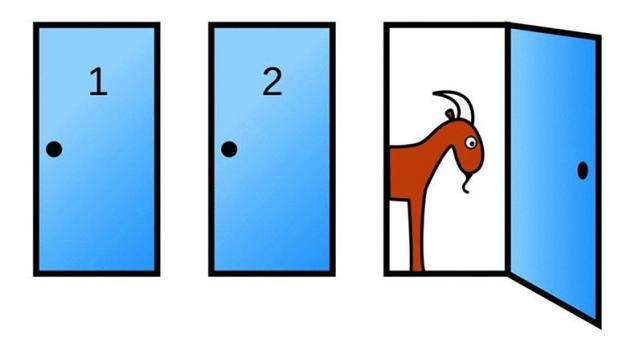
The Monty Hall problem is Exactly this problem in the film "Twenty-one" suggested crafty MIT Professor. Giving the correct answer, the main character falls into the group of brilliant young mathematicians, play a casino in Las Vegas.
The classic formulation is: "Suppose a certain player is invited to take part in the famous American TV show Let's Make a Deal, which leads Monty Hall, and he must choose one of three doors. Behind two doors are goats, behind one is the prize, the car, the presenter knows the location of the prizes. After the player makes his choice, the presenter opens one of the remaining doors, behind which is a goat, and offers the player to change his mind. Should the player agree or it is better to keep your initial choice?"
Here is a typical line of reasoning: after the host has opened a door and showed a goat, the player has to choose between two doors. The car is behind one of them, then the probability of its guessing is½. So there is no difference — to change your choice or not. Nevertheless, probability theory says that it is possible to increase your chances of winning by changing the decision. We will understand why this is so.
This back a step. In that moment, when we made our initial selection, we have divided the doors into two parts: the chosen and the other two. It is obvious that the probability that the car is hiding behind "our" door is⅓, respectively, the car is behind one of the two remaining doors with probability⅔. When the host reveals that behind one of those doors is a goat, it turns out that the ⅔ chance be in the second door. And it drives the player's choice of two doors, behind one of which (initially selected) the car is with a probability of⅓, and the other with a probability of⅔. The choice becomes obvious. That, of course, does not negate the fact that from the beginning the player can choose the door with the car.

The problem of three prisoners Paradox three prisoners similar to the Monty Hall problem, although the action takes place in more dramatic conditions. Three prisoners (A, B, and C) sentenced to death and placed in solitary confinement. The Governor randomly selects one of them and gives him a pardon. The warden knows which one of the three pardoned, but he was told to keep it a secret. Prisoner A asks the guard to tell him the name of the second prisoner (except himself), who will definitely be executed: "if pardoned, tell me what will be executed If pardoned, tell me that the executed will be B. If they will both be executed and pardoned me, toss a coin, and tell any of these two names." The warden says that the prisoner will be executed B. Should we rejoice for the prisoner, Eh?
It would seem, Yes. After receiving this information, the probability of death of a prisoner And was⅔, and now he knows that one of the other two prisoners will be executed — hence the probability of his execution has decreased to½. But in fact a prisoner And not learned anything new: if he is not pardoned, he will call the name of another prisoner, and so he knew that someone of the remaining two will be executed. If he was lucky, and the execution was canceled, he hears a random name B or C. Therefore, his chance for salvation has not changed.
Now imagine that someone of the remaining prisoners know about the prisoner question and answer. It will change his view on probability of pardon.
If the conversation overheard prisoner B, he learns that his precisely executed. And if the prisoner, then the probability of pardon will be⅔. Why did this happen? The prisoner And received no information, and his chances for a pardon is still⅓. The prisoner would certainly not be pardoned, and his chances are zero. So, the likelihood that freedom will be released the third prisoner, is equal to⅔.

The two envelopes paradox This paradox has become known thanks to the mathematics of Martin Gardner, and stated as follows: "Suppose you and another offered two envelopes, one of which is a certain amount of money X and the other with the amount twice. You have independently from each other open the envelopes, count the money, and then can exchange them. The envelopes are the same, so the likelihood that you will get the envelope with the smaller amount, is½. Suppose you opened the envelope and found a $10. Consequently, in the envelope your friend may be equally probable $5 or $20. If you decide to exchange, it is possible to calculate the mathematical expectation of the total amount — that is, its average value. It is 1/2x$5+1/2×20=$12,5. Thus, the exchange is beneficial to you. And, most likely, your friend will reason the same way. But it is obvious that the exchange may not be beneficial to you both. What is the error?"
The paradox is that until you opened your envelope, the probabilities behave good: you do have a 50% chance to find in your envelope the amount X 50% amount 2X. And common sense tells us that information about the current amount can not affect the contents of the second envelope.
However, as soon as you open the envelope, the situation changes drastically (this paradox is somewhat similar to the story of Schrodinger's cat, where the very presence of an observer affects the situation). The fact that compliance with the terms of the paradox the probability of finding the second envelope to a greater or lesser amount, than you, should be the same. But then equally likely any value of this sum from zero to infinity. But if equally infinite number of possibilities, their sum is infinity. But this is impossible.
For clarity, you can imagine that you find in your envelope one cent. It is obvious that the second envelope can not be the amount in half.
Interestingly, discussions regarding resolution of the paradox continue in the present. At the same time attempts how to explain the paradox from within and to develop the best strategy in this situation. In particular, Professor Thomas Cover proposed an original approach to strategy formation — to change or not to change the envelope, guided by a kind of intuitive expectation. For example, if you opened the envelope and found a $10 — a small amount of your estimates — it is worth it to exchange. And if the envelope is, say, $1 000 that exceeds your wildest expectations, then change is not necessary. This intuitive strategy is in case you regularly offer to choose two of the envelope, makes it possible to increase the total gain is more than the strategy of constant change envelopes.

Paradox boys and girls This paradox was proposed by Martin Gardner and is formulated as: "Mr. Smith has two children. At least one child — a boy. What is the probability that the second is also a boy?"
It would seem that the task is simple. However, if you start to understand, revealed a curious fact: the correct answer will differ depending on how we calculate the probability of the sex of the other child.
Option 1
Consider all the possible combinations in families with two children:
— Girl/Girl
— Girl/Boy
— Boy/Girl
— Boy/Boy
The option girl/girl doesn't fit us for this task. Therefore, for the family of Mr. Smith, there are three equally likely options — and, therefore, the probability that the other child also being a boy, is⅓. This answer was given by Gardner initially.
Option 2
Imagine that we meet Mr Smith on the street when he walks with his son. What is the probability that the second child — also a boy? Since the sex of the second child does not depend on the sex of the first, the obvious (and correct) answer is½.
Why this happens, because it would seem that nothing has changed?
It all depends on how we approach the issue of counting probability. In the first case we considered all possible variants of the Smith family. Second, we considered all the families falling under the obligatory "must be a boy". The calculation of the probability of sex of the second child was carried out with this condition (in probability theory this is called "conditional probability"), which led to the result that is different from the first. published
P. S. And remember, only by changing their consumption — together we change the world! © Join us at Facebook , Vkontakte, Odnoklassniki
Source: theoryandpractice.ru/posts/7518-paradoks-probability

The Monty Hall problem is Exactly this problem in the film "Twenty-one" suggested crafty MIT Professor. Giving the correct answer, the main character falls into the group of brilliant young mathematicians, play a casino in Las Vegas.
The classic formulation is: "Suppose a certain player is invited to take part in the famous American TV show Let's Make a Deal, which leads Monty Hall, and he must choose one of three doors. Behind two doors are goats, behind one is the prize, the car, the presenter knows the location of the prizes. After the player makes his choice, the presenter opens one of the remaining doors, behind which is a goat, and offers the player to change his mind. Should the player agree or it is better to keep your initial choice?"
Here is a typical line of reasoning: after the host has opened a door and showed a goat, the player has to choose between two doors. The car is behind one of them, then the probability of its guessing is½. So there is no difference — to change your choice or not. Nevertheless, probability theory says that it is possible to increase your chances of winning by changing the decision. We will understand why this is so.
This back a step. In that moment, when we made our initial selection, we have divided the doors into two parts: the chosen and the other two. It is obvious that the probability that the car is hiding behind "our" door is⅓, respectively, the car is behind one of the two remaining doors with probability⅔. When the host reveals that behind one of those doors is a goat, it turns out that the ⅔ chance be in the second door. And it drives the player's choice of two doors, behind one of which (initially selected) the car is with a probability of⅓, and the other with a probability of⅔. The choice becomes obvious. That, of course, does not negate the fact that from the beginning the player can choose the door with the car.

The problem of three prisoners Paradox three prisoners similar to the Monty Hall problem, although the action takes place in more dramatic conditions. Three prisoners (A, B, and C) sentenced to death and placed in solitary confinement. The Governor randomly selects one of them and gives him a pardon. The warden knows which one of the three pardoned, but he was told to keep it a secret. Prisoner A asks the guard to tell him the name of the second prisoner (except himself), who will definitely be executed: "if pardoned, tell me what will be executed If pardoned, tell me that the executed will be B. If they will both be executed and pardoned me, toss a coin, and tell any of these two names." The warden says that the prisoner will be executed B. Should we rejoice for the prisoner, Eh?
It would seem, Yes. After receiving this information, the probability of death of a prisoner And was⅔, and now he knows that one of the other two prisoners will be executed — hence the probability of his execution has decreased to½. But in fact a prisoner And not learned anything new: if he is not pardoned, he will call the name of another prisoner, and so he knew that someone of the remaining two will be executed. If he was lucky, and the execution was canceled, he hears a random name B or C. Therefore, his chance for salvation has not changed.
Now imagine that someone of the remaining prisoners know about the prisoner question and answer. It will change his view on probability of pardon.
If the conversation overheard prisoner B, he learns that his precisely executed. And if the prisoner, then the probability of pardon will be⅔. Why did this happen? The prisoner And received no information, and his chances for a pardon is still⅓. The prisoner would certainly not be pardoned, and his chances are zero. So, the likelihood that freedom will be released the third prisoner, is equal to⅔.

The two envelopes paradox This paradox has become known thanks to the mathematics of Martin Gardner, and stated as follows: "Suppose you and another offered two envelopes, one of which is a certain amount of money X and the other with the amount twice. You have independently from each other open the envelopes, count the money, and then can exchange them. The envelopes are the same, so the likelihood that you will get the envelope with the smaller amount, is½. Suppose you opened the envelope and found a $10. Consequently, in the envelope your friend may be equally probable $5 or $20. If you decide to exchange, it is possible to calculate the mathematical expectation of the total amount — that is, its average value. It is 1/2x$5+1/2×20=$12,5. Thus, the exchange is beneficial to you. And, most likely, your friend will reason the same way. But it is obvious that the exchange may not be beneficial to you both. What is the error?"
The paradox is that until you opened your envelope, the probabilities behave good: you do have a 50% chance to find in your envelope the amount X 50% amount 2X. And common sense tells us that information about the current amount can not affect the contents of the second envelope.
However, as soon as you open the envelope, the situation changes drastically (this paradox is somewhat similar to the story of Schrodinger's cat, where the very presence of an observer affects the situation). The fact that compliance with the terms of the paradox the probability of finding the second envelope to a greater or lesser amount, than you, should be the same. But then equally likely any value of this sum from zero to infinity. But if equally infinite number of possibilities, their sum is infinity. But this is impossible.
For clarity, you can imagine that you find in your envelope one cent. It is obvious that the second envelope can not be the amount in half.
Interestingly, discussions regarding resolution of the paradox continue in the present. At the same time attempts how to explain the paradox from within and to develop the best strategy in this situation. In particular, Professor Thomas Cover proposed an original approach to strategy formation — to change or not to change the envelope, guided by a kind of intuitive expectation. For example, if you opened the envelope and found a $10 — a small amount of your estimates — it is worth it to exchange. And if the envelope is, say, $1 000 that exceeds your wildest expectations, then change is not necessary. This intuitive strategy is in case you regularly offer to choose two of the envelope, makes it possible to increase the total gain is more than the strategy of constant change envelopes.

Paradox boys and girls This paradox was proposed by Martin Gardner and is formulated as: "Mr. Smith has two children. At least one child — a boy. What is the probability that the second is also a boy?"
It would seem that the task is simple. However, if you start to understand, revealed a curious fact: the correct answer will differ depending on how we calculate the probability of the sex of the other child.
Option 1
Consider all the possible combinations in families with two children:
— Girl/Girl
— Girl/Boy
— Boy/Girl
— Boy/Boy
The option girl/girl doesn't fit us for this task. Therefore, for the family of Mr. Smith, there are three equally likely options — and, therefore, the probability that the other child also being a boy, is⅓. This answer was given by Gardner initially.
Option 2
Imagine that we meet Mr Smith on the street when he walks with his son. What is the probability that the second child — also a boy? Since the sex of the second child does not depend on the sex of the first, the obvious (and correct) answer is½.
Why this happens, because it would seem that nothing has changed?
It all depends on how we approach the issue of counting probability. In the first case we considered all possible variants of the Smith family. Second, we considered all the families falling under the obligatory "must be a boy". The calculation of the probability of sex of the second child was carried out with this condition (in probability theory this is called "conditional probability"), which led to the result that is different from the first. published
P. S. And remember, only by changing their consumption — together we change the world! © Join us at Facebook , Vkontakte, Odnoklassniki
Source: theoryandpractice.ru/posts/7518-paradoks-probability
In anticipation of better times...
The revelation of the beekeeper: Honey deception, learn the truth!