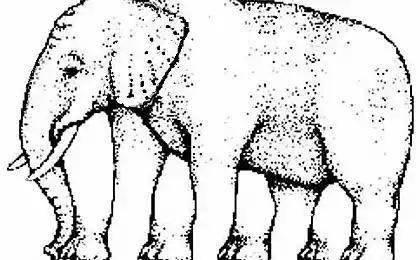
1903
12 неймовірних парадокс

Парадокс існував з часів давньогрецьких За допомогою логіки можна швидко знайти жирний недолік в парадоксі, який показує, чому здавалося б неможливе можливе або що весь парадокс просто будується на недоліках мислення.
Чи можна зрозуміти недолік кожного з наступних парадоксів?
12. Парадокс Оберса
У астрофізиці та фізиці, парадокс Ольберса є аргументом, що темрява нічного неба з припущенням нескінченного і вічного статичного Всесвіту. Це один доказ нестатичного Всесвіту, таких як сучасна модель Big Bang. Цей аргумент часто згадується як «тежний парадокс нічного неба», який говорить про те, що з будь-якого кута з Землі, лінія пам'ятки буде завершена, коли він досягає зірки.
Щоб зрозуміти це, ми порівняємо парадокс, щоб знайти чоловіка в лісі серед білих дерев. Якщо, з будь-якої точки зору, лінія пам'яток закінчується на вершинах дерев, вона все одно бачить тільки білий? Це суперечить темряві нічного неба і змушує багатьох людей дивувати, чому ми не тільки бачимо світло від зірок в нічному небі.
11. Парадокс омніпотенції
Парадокс є те, що якщо він може виконувати будь-які дії, то він може обмежити свою здатність виконувати їх, тому не може виконувати всі дії, але з іншого боку, якщо він не може обмежувати свої дії, то це те, що він не може робити.
Здавалося б, що здатність омніпотента обмежувати себе обов'язково означає, що він дійсно обмежує себе. Цей парадокс часто сформульований в термінології абраземічних релігій, хоча це не вимога.
Один варіант парадоксу омніпотенції є так званим кам'яним парадоксом: може бути омніпотентом, щоб створити камінь так важко, що навіть він не зможе піднімати його? Якщо так, як перестає бути омніпотентом, і якщо ні, що не було омніпотентом з початку.
Відповідь на парадокс це: наявність слабкості, таких як нездатність піднімати важке камінь, не потрапляє в категорію омніпотенції, хоча визначення омніпотенції передбачає відсутність слабких сторін.
10. Парадокс Соріта
Парадокс це: розгляньте палицю піску, з якого поступово видаляють зерна піску. Ви можете побудувати аргументацію за допомогою виписок:
1,000,000 зерна піску - це пальня піску.
Плитка піщаного фаршу одна з зерна піску ще є пальцем піску.
Якщо продовжити другу дію без зупинки, то, в кінцевому підсумку, це призведе до того, що паль буде складатися з одного зерна піску. На перший погляд існує кілька способів уникнути цього висновку. Один може об'єднатися до першого приміщення, кажучи про те, що мільйон зерна піску не є пальцем. Але замість 1000000 може бути довільно інший великий номер, а другий заява буде вірним для будь-якого числа з будь-яким числом нулів.
Таким чином, відповідь повинна явно заперечувати існування таких речей, як палі. Крім того, один може об'єднатися до другої хибки, що він не вірний для всіх «зернових збірок» і що знімання одного зерна або зерна піску все ще залишає за собою ковпачок. Або це може стверджувати, що пальня піску може складатися з цільного зерна піску.
9. Навігація Парадокс цікавих чисел
Заява: не така річ, як незаміжній природний номер.
Всупереч: Якщо у вас є незрівнянний набір натуральних чисел, які безперешкодно. У зв'язку з властивостями натуральних чисел, список вихідних чисел обов'язково буде мати найменше число.
Як і найменша кількість набору, її можна визначити як цікавіше в цьому комплекті незаміжніх чисел. Ми приїхали до суперечності, оскільки найменше число не може бути як цікавим, так і безперешкодним. Таким чином, набори неперервних чисел повинні бути порожніми, допускаючи, що немає такої речі, як незворотні номери.
8. У Парадокс літаючої стріли
Цей парадокс передбачає, що для того, щоб відбуватися рух, об'єкт повинен змінити позицію, яку він займає. Приклад - рух стріли. У будь-який час літаюча стрілка залишається стаціонарним, тому що вона перебуває в стані спокою, і так як вона перебуває в стані спокою в будь-який час, вона завжди стаціонарна.
Що таке парадокс, висувається Zeno в 6 столітті, говорить про відсутність руху так, виходячи з того, що рухоме тіло повинно досягати половини перед завершенням руху. Але з тих пір, поки він не закріпився, Цей парадокс також відомий як парадокс Fletcher.
Варто відзначити, що якщо попередні парадокси були про космос, то наступний парадокс про ділення часу не в сегменти, а в точки.
7. Про нас Парадокс Ахіллс і черепаха
У цьому парадоксі, Ахіллс працює після черепахи, попередньо давши йому початок голови 30 метрів. Якщо ми припустимо, що кожен з бігунів почав працювати на певній постійній швидкості (тільки дуже швидко, другий дуже повільно), то після того, як Achilles, бігти 30 метрів, досягне точки, з якої черепаха переїхала. У цей час черепаха буде бігати набагато менше, скажуть, 1 метр.
Після того, як Achilles буде потрібно більше часу, щоб подолати цю відстань, під час якої черепаха буде рухатися ще далі. Досягнувши третій момент, який побував на черепахі, Ахіллс буде далі, але все ще не захопить його. Так, коли Ахіллс досягає крутого удару, вона все ще буде попереду.
Таким чином, так як є нескінченна кількість точок, які повинні доходити Агіллі, і які черепахи вже відвідали, він ніколи не зможе зловити черепахою. Звісно, логіка розповідає нам, що Achilles може зловити черепаху, тому це парадокс.
Проблема з цим парадоксом полягає в тому, що в фізичній реальності неможливо перетнути точку безкінечно – як можна отримати з однієї точки нескінченності до іншого без переправлення нескінченності точок? Не можна, тому це неможливо.
Але це не вірно в математику. Цей парадокс показує нам, як математика може довести щось, але це не дійсно працює. Таким чином, проблема з даним парадоксом полягає в тому, що математичні правила застосовуються до нематематичних ситуацій, що робить його непрацюваним.
6. Жнівень Парадокс Бурідан
Це метафорний опис людської недостатності. Це відноситься до парадоксальної ситуації, коли додака, будучи між двома абсолютно ідентичними за розмірами і якісними гайстаками, буде зірватися до смерті, так як він не зможе приймати раціональне рішення і почати їсти.
Парадокс названий 14-го століття французьким філософом Жаном Буріданом, але він не був автором парадоксу. Він був відомий з часів Арістоле, який в одному з його творів розповідає про чоловіка, який був голодним і молочним, але так як обидва почуття були однаково міцними, і чоловік був між їжею і напою, він не міг зробити вибір.
Бурідан, в свою чергу, ніколи не говорили про проблему, але підняли питання про моральний детермінізм, які нав'язують, що людина, зіткнулася з проблемою вибору, обов'язково повинні вибрати в напрямку більшого хорошого, але Бурідан дозволив можливість сповільнити вибір, щоб оцінити всі можливі переваги. Пізніше інші письменники задовольнять цей вид, говорять про донечку, що, зіткнувшись з двома ідентичними хастаками, порушують приймати рішення.
5. Умань Парадокс невибагливого виконання
Суддя розповідає про засуджений, що він буде вішати в нооні на одному з робочих днів наступного тижня, але день виконання буде несподіваним. Він не знає точної дати, поки виконавець надійде до його комірки на нооні. Після невеликої причини злочинець приходить до висновку, що він може уникнути виконання.
Його причини можна розділити на кілька частин. Він починає говорити про те, що він не може повісити в п'ятницю, бо якщо він не повісився в четвер, п'ятниця не буде сюрпризом. Так п'ятниця виправила. Але після цього, з п'ятниці вже застрягнув список, він уклав, що він не міг повісити в четвер, бо якщо він не повісився в середу, то четвер не буде сюрпризом.
Так, він послідовно виключив всі інші дні тижня. Зрозуміло він йде на ліжко з певністю, що виконання не відбудеться взагалі. Наступного тижня, в нооні на середу, виконавець прийшов до свого осередку, тому, незважаючи на всі його причини, він був надзвичайно дивним. Все суддя сказав:
4. У Парадокс барбера
Попри те, що є місто з одним чоловічим барбером, і що кожен людина в місті потілює голову: деякі на власній, деякі з допомогою перукаря. Здається розумно припустити, що процес заперечує наступне правило: барбер подрібнює всіх чоловіків і тільки тих, хто не погострить себе.
У цьому сценарії ми можемо запитати наступне питання: Чи сам барбер? Однак, запитуючи це, ми усвідомлюємо, що неможливо відповісти правильно:
Якщо барбер не поготував себе, він повинен дотримуватися правил і поголівити себе.
Якщо він сам поголює, він не поготував себе.
3. У Парадокс епіменидів
Цей парадокс слідує за заявою, в якій Епімениди, всупереч поширеній вірі Кріте, запропонував, що Зеус був безсмертним, як і в наступному вірші:
Вони створили для вас горб, високий святого.
Крітани, вічні зв'язки, злий звір, раби шлунка!
Але ви не мертві, ви живі і будете жити назавжди.
Для вас жити в нас і ми є.
Він не усвідомив, що у виклику всіх криштів Кританів, він невпинно назвав себе одержувачем, хоча він «покраплений», що всі вони були крім нього. Таким чином, якщо ви вважаєте його заявою, і всі Крітани несуть, то він також є крилом, і якщо він є крилом, то всі Крітани говорять про правду. Так, якщо всі Кртани розповідають правду, він говорить про правду, що означає, що всі Кртани є брехні. Таким чином, ланцюжка примірки повертається на початок.
2. Парадокс Евата
Це дуже стара проблема в логіці, стебло з давньої Греції. Він сказав, що знамениті софісти Протагори взяли Євта до його викладання, але він чітко розумів, що студент зможе платити вчителя тільки після того, як він виграв свій перший випадок в суді.
Деякі експерти стверджують, що Protagoras вимагали гроші на навчання відразу після того, як Evatl закінчив свої дослідження, інші стверджують, що Protagoras чекав на той час, поки не стало очевидним, що студент не докладав зусиль для пошуку клієнтів, а інші вважають, що Evatl спробував дуже важко, але ніколи не знайшов клієнтів. У будь-якому випадку, Protagoras вирішили відмовитися від заборгованості.
Прогагори заявили, що якщо він виграв справу, він буде платити його гроші. У випадку, якщо у вас виникли питання про тегори, до того ж було б отримати свої гроші відповідно до оригінального контракту, оскільки він був першим виграшним кейсом Evatl.
У Evatl, однак, наполягати, що якщо він виграв, він не доведеться платити Протагори за наказом суду. Якщо, з іншого боку, Protagoras перемагає, Evatl втратив свій перший випадок, тому він нічого не повинен платити. Який чоловік правий?
1,1 км Парадокс нестійкої сили
Парадокс форс-мажор - класичний парадокс, розроблений як “що відбувається, коли нездатна сила відповідає незнімному об'єкту?” Парадокс повинен розумітися як логічні вправи, а не як післяутворення можливої реальності.
Згідно з сучасними науковими розуміннями, жодна сила абсолютно нездатна, і не може бути абсолютно незнімними предметами, так як навіть невелика сила призведе до невеликого прискорення об'єкта будь-якої маси. Фіксований об'єкт повинен мати нескінченну інерцію і тому нескінченну масу. Такий об'єкт буде стиснений власною вагою. Нездатна сила вимагає нескінченної енергії, яка не існує в скінченному Всесвіті.