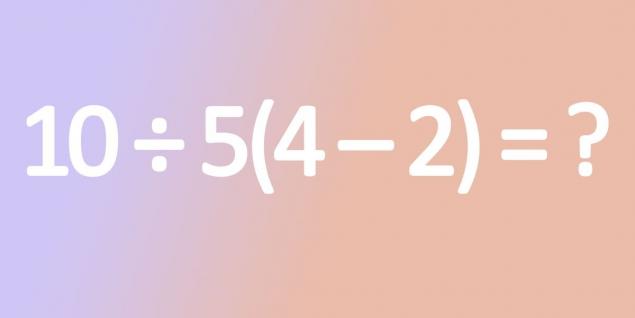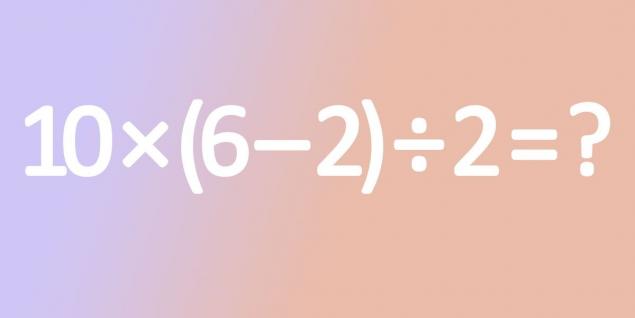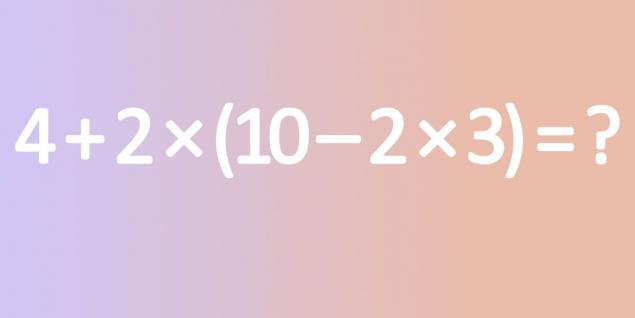Ніч Я сперечався з чоловіком, як вирішити приклади з кронштейнами, він зумів прокидати світло на важливе математичне питання.

Вирішення прикладів з кронштейнами Діти вже у другому класі. І хоча всі ці знання згодом фіксуються у вирішенні складних прикладів, іноді це не дає відчутного результату. І дитина не навчає основних принципів рішення. А отже, у дорослому віці не можна впоратися з такими завданнями.

Сьогодні видання. "Сайт" Я хотів би вирішити кілька прикладів з кронштейнами. В той же час ми пам'ятаємо, які правила слідувати в цьому випадку. І в цілому такий невеликий математичний прогрів досить корисний для розуму. Тому ми радимо регулярно вирішувати цікаві проблеми і приклади для дорослих і дітей.

3610Р. 4200Р.

Вирішення прикладів з кронштейнами

1. Перша задача досить проста. Тим не менш, брекети здатні заплутуватися навіть визнаючи добро, не кажучи вже про тертіар, особливо два. Спробуйте вирішити цей приклад крок за кроком без отримання однієї помилки.
   
   
   
   
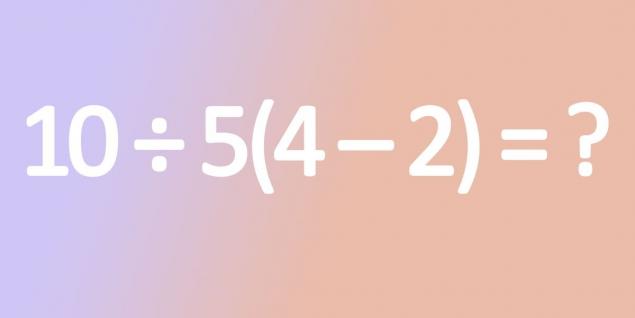
2. У другому задачі знову є скоби, і поділ, і багатозастосування. Тим не менш, вам доведеться виконувати математичні операції в іншому порядку. Намагайтеся запам'ятати необхідні правила, щоб слідувати за цією ситуацією. Пам'ятайте, що існує тільки одна вірна відповідь.
   
   
   
   
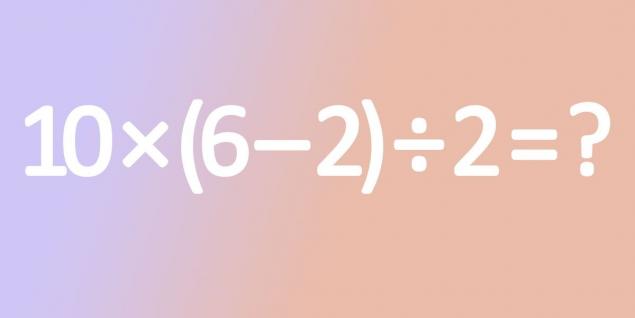
3. Третій приклад більш складний. Але якщо ви знаєте, які дії виконувати в якому порядку, то легко знайти відповідь. Також пам'ятайте про те, щоб перевірити наші пояснення та відповіді в другій частині статті.
   
   
   
   

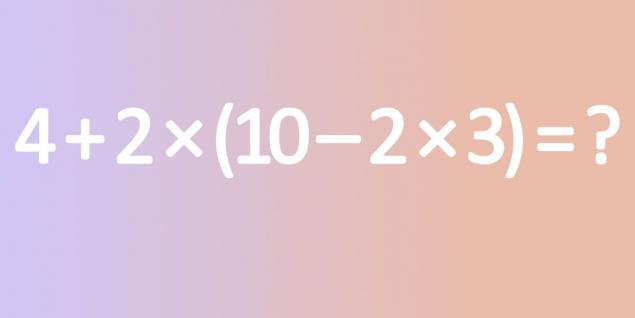
Перш за все, давайте згадувати прості правила, які багато дорослих можуть вже забути. Якщо на прикладі немає брекетів, то всі математичні операції виконуються зліва направо. Але в той же час поділ і багатозастосування виконуються відразу, а крім і відступу пізніше.

На прикладах з кронштейнами все трохи складніше, але небагато. Тут ми спочатку робимо все в дужках (як описано вище), а потім виконуємо всі математичні операції зліва направо, враховуючи, що поділ і багатозастосування знову мають більш високий пріоритет.

1. З огляду на описані алгоритми, в першому задачі ми спочатку виконуємо дії в дужках, потім ділимо, і тільки помножуємо в самому кінці. Так ми отримуємо: 10 ÷ 5 × 2 = 2 × 2 = 4.
2. У другому прикладі ми вперше виконуємо дії в дужках, потім розмножуємо, і тільки нарешті ділимося. В результаті наш приклад стає наступним чином: 10 × 4 ÷ 2 = 40 ÷ 2 = 20.
3. Тепер останній приклад, ймовірно, не зданий читачеві як страшний. По-перше, ми розраховуємо, що в дужках ми маємо 10 – 2 × 3 = 10 – 6 = 4. Потім весь приклад вирішується наступним чином: 4 + 2 × 4 = 4 + 8 = 12.
   
   
   
   

Ми сподіваємося, що зараз рішення прикладів з кронштейнами не складе труднощів для вас. І якщо ви думаєте, що ці завдання занадто прості, то спробуйте вирішити більш складні приклади, які ми опублікували нещодавно. Чи не можна робити помилки? Не забудьте поділитися своїми рішеннями в коментарях.