Парадоксичні математичні проблеми, рішення яких суперечать поширеним почуттям

У математикі існує безліч прикладів ситуацій, які можуть існувати в реальності, але не мають логічних пояснень, і таким чином кладуть нас в повному просуванні.

Проблемні проблеми допоможуть вам перевірити свої психічні здібності:

1,1 км Уявіть, що ви в шоу, де ведуться три двері. За однією з дверей є приз - новий автомобіль, а за два залишилися - дві кози. Ви можете вибрати будь-які двері і отримати приз за ним.

Ви забираєте двері, а потім господар відкриває одну з інших двох дверей (хост знає, куди ховається автомобіль, але він завжди відкриває одну за кози).







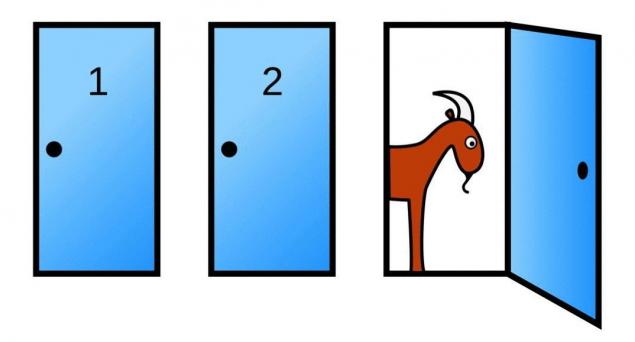
Ведучий запитує вас:

до Ви хочете змінити свій вибір?

до Ви хочете зупинитися на одному з дверей, які ви вибрали?

Ваше рішення?

Так ви вирішили залишити попередній вибір.

• Не існує різниці між зміною дверей або ні.
  
  
• З двома дверцятами зліва, ймовірність вгадати, де автомобіль знаходиться 50/50.
  
  
• Право?
  
  

544962



Вронг!

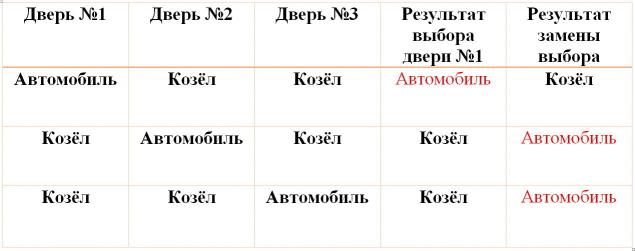
р.



Правильна відповідь полягає в тому, що ви завжди повинні змінити свій вибір, тому що ви двічі, як правило, можете виграти автомобіль.

• Якщо він спочатку вибирає двері, за якими знаходиться автомобіль.
  
  
• Так як ймовірність вибору автомобіля на першому етапі є одним в трьох (або 33%), шанс не вибрати автомобіль, якщо гравець змінив свій вибір також в трьох (або 33%).
  
  
• Це означає, що гравець, який використовує стратегію зміни дверей, має 66% або два-три шанси виграти.
  
  
• Це подвоює шанси виграти гравця, стратегія якого не змінює свій вибір.
  
  

Як не вірити? Давайте скажемо, вибираємо двері No 1. Ось всі можливі варіанти, які можуть статися в цьому випадку:

Р



Якщо ви залишите свій оригінальний вибір, ви переможете один з трьох; якщо ви зміните свій вибір, ви вгадаєте двічі з трьох.

Ви все ще не впевнені? Давайте зробимо те ж саме з 50 дверима. Вибираємо двері No 1.





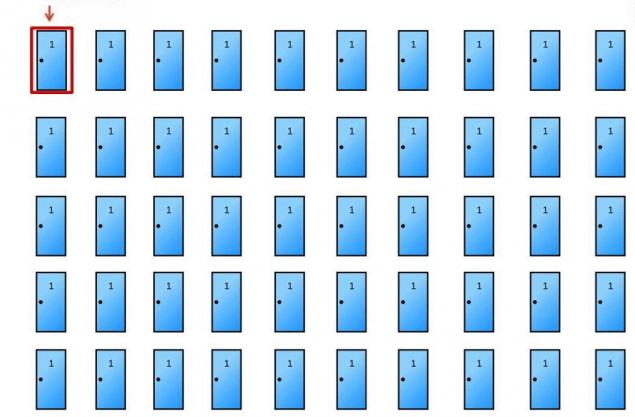
І ми відкриваємо інші 48 дверей з кізами, прихованими за ними. Ви все ще впевнені у виборі? Пам'ятайте, у вас є 1 в 50 шанс згадати праві двері на перший раз. Те ж саме принцип діє тут.





Звичайно, гра має на увазі, що ви бажали виграти автомобіль, а не коза.

2,2 км Ви працюєте в офісі з 23 працівниками, включаючи вас. Яка ймовірність того, що два співробітники будуть однакові дні народження?

(Ми не враховуємо 29 лютого)

Ваша команда 23 співробітників (ви маєте номер 14):





Імовірність, що два люди в офісі мають день народження в той же день - 50%.

• Якщо кількість людей досягає фігури 366, то статистично гарантовано гарантується, що принаймні два люди будуть мати однаковий день народження, так як можливо тільки 365 ймовірних іменинників.
  
  
• Однак якщо ви вважаєте, що всі дні народження можуть бути однаково ймовірними, то для групи 57 осіб ймовірність такої збігу становить 99%.
  
  

Як дізнатися?

• Повернемося до 23 колег в офісі, щоб побачити, як це можливо.
  
  
• Поперечно, не два люди в групі будуть мати той же день народження.
  
  
• З'ясуйте ймовірність, що принаймні два люди в офісі святкують День народження в той же день дуже складно, коли стикаються з ним безпосередньо.
  
  
• З'ясуйте ймовірність, що ніхто не в групі має такий же день народження набагато простіше.
  
  

Імовірність того, що два люди не мають такого ж дня:





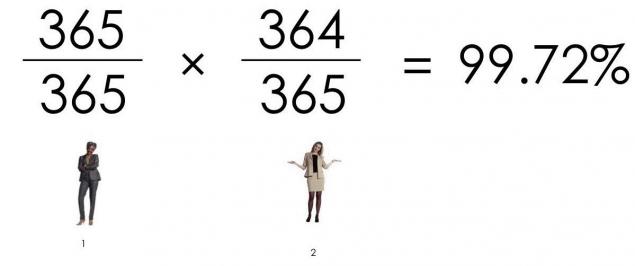
Імовірність, що три люди не мають такого ж дня:





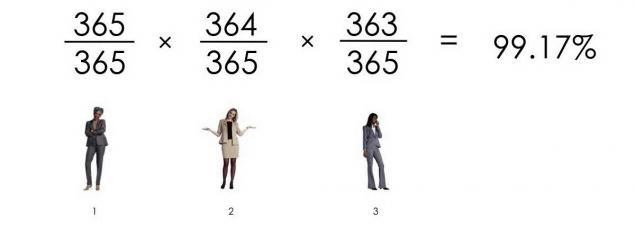
Імовірність, що чотири люди мають різні дні народження:





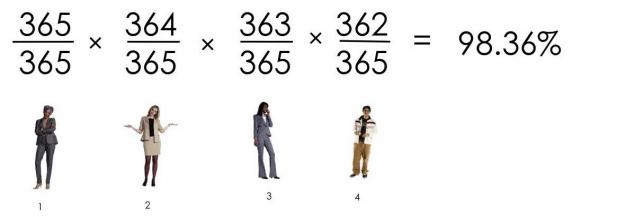
Що ми отримуємо? Імовірність, що 23 людей мають різні дні народження:





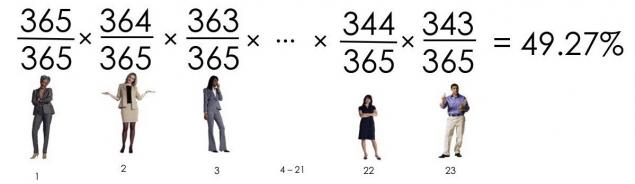
З шансу, що ніхто не народився на той же день, 49,3%, ймовірність, що принаймні два люди мають однаковий день народження 50,7%.

Ось чого виглядає крива ймовірність:



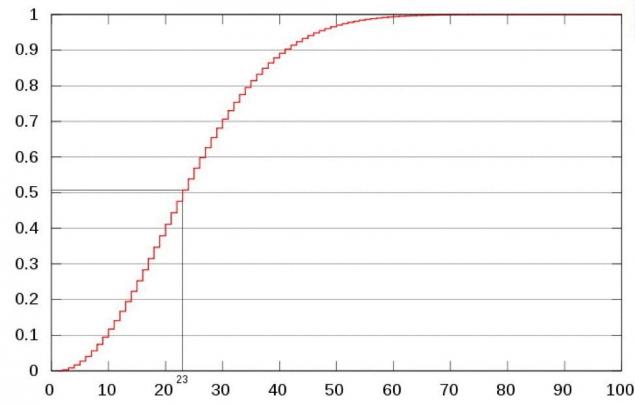
Вертикалізація: ймовірність пар; горизонтальна: кількість людей

3. У Наприклад, на мові соціальних мереж люди, які слідують користувачем, і ті, хто слідує йому, мають більш послідовники, ніж він сам.

• Цей феномен заснований на ідеї, що більшість людей мають менше друзів, ніж їхні друзі.
  
  
• У 1991 році соціолог Скотт Фельд зробив несподіване відкриття. 74% людей мають менше друзів, ніж їхні друзі.
  
  

Давайте подивимося на цю заяву з прикладом. Це знову офіс з 20 працівниками (припустимо, три інші були вогнеті). Лінії на малюнку вказують, хто друзів з ким в офісі.

Графік дружніх відносин:





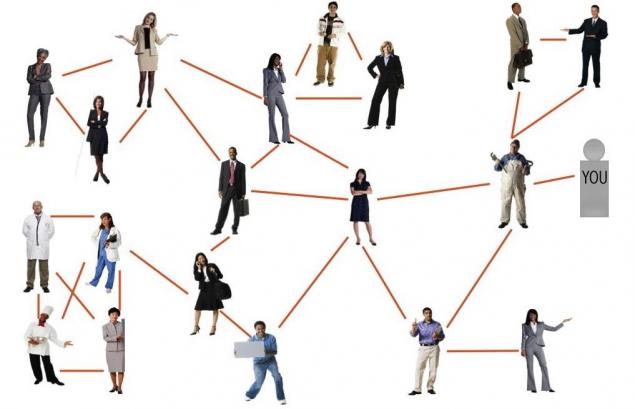
Середній працівник має 2,85 друзів. Однак середня кількість друзів людина має 3.39.

Це люди, які мають середню кількість друзів, як показано вище. Тому вони найбільш популярні члени групи. Але найголовніше, 17 з 20 осіб в офісі друзів не менше одного з цих людей:





Це просто приклад, але в реальному житті він також знаходить підтвердження.

• У Twitter люди, які ви стежите, швидше за все, мають більше послідовників, ніж ви. Те ж саме відбувається з друзями на Facebook або Vkontakte.
  
  
• По суті, ви, швидше за все, повинні бути друзями з ким-небудь, хто має велику кількість друзів, ніж з ким-небудь, хто має невелику кількість друзів.
  
  
• Цей парадокс також поширюється на сексуальні стосунки.
  
  
• Якщо середня людина має сексуальні зв’язки з чотирма іншими людьми та іншим «незнімним» партнером, їх сексуальні партнери будуть, в середньому, мають більш сексуальні партнери, ніж вони насправді роблять через людину, яка має промісний секс.
  
  

4. У Цей парадокс був першим опублікований математиком Мартіном Гарднером у його 1959 році Науковий американський математичний ігровий стовпчик.

Трьох в'язнів, А, Б і С, в солітарному співвідношенні і засуджених до смерті. Намісник випадково обирає один з них і його пародонти. В'язниця знає, хто був запалений, але він не має права сказати так.

• Як найвагоміший, ув'язнений А просить охорону розповісти йому ім'я в'язниці (Б або С), які будуть виконані.
  
  
• В'язниця Пропозиції, "Якщо B парадонований, розкажіть, що C буде виконано. Якщо C є пародонтом, скажіть, що B буде виконано. Якщо я вказав, що монета і дати будь-яке ім'я.
  
  
• охоронець підкаже ув'язненим А, що в'язниця Б буде виконана.
  
  

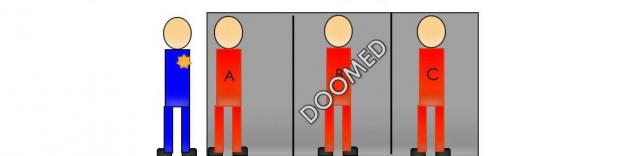
• В'язниця Збуджена, тому що зараз ймовірність його виживання є 1/2, не 1/3, як одна з в'язнів, A або C, буде приурочена.
  
  
• В'язниця Імовірно розповідає в'язнів К, що Б буде виконано. В'язниця Це також анотація, оскільки він все ще вірить в'язниці Ймовірність виживання 1/3 і його ймовірність виживання зросла до 2/3.
  
  

Що це неправильно?

Відповідь: Тюрма S право.

1) Спочатку всі три в'язниці мають одну з трьох шансів бути принесені. В'язниця заявила, що в'язниця B буде виконана, що означає, що події розгортаються в одному з двох сценаріїв:

C буде pardoned (1 шанс з 3)

- А буде припаркований і монета показала "B" (1 шанс з 6)

1 час Це означає, що шанси, що в'язниця А буде приурочена, є пів шансів, що C буде приурочена. І в'язниця B не має шансів бути приурочена.

(3) Таким чином, ймовірність того, що А після того, як пардоне залишається незмінною – 1/3, при цьому ймовірність того, що C посилюється до 2/3.

Якщо ви ще не сумніваєтеся, подивіться на повний список тюрмортів:

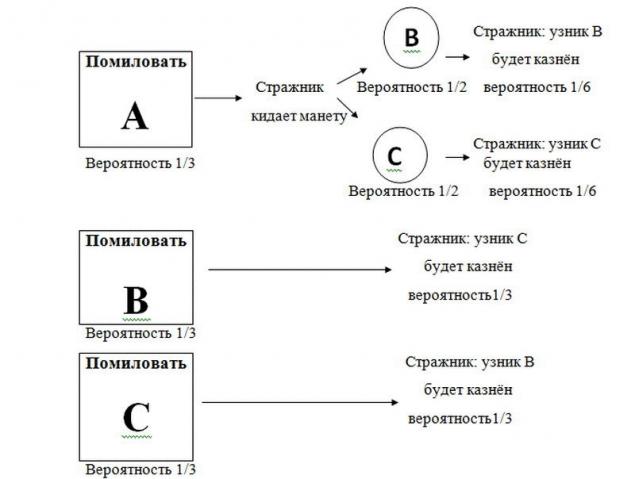р.



І якщо ми подивимося на прикладі, де охоронець каже, що в'язниця B буде виконана, ми бачимо, що в'язниця C двічі, як ймовірно, буде підпорядкована як в'язниця A:





З тих пір, як ми знаємо, що B має шанс 0% бути пардоненим, і це C, як правило, є пардонімом як A, потім:

The Guard коментує B буде виконано.







5. Умань Ідеальна паралелограма з чотиристороннього полігона Намалюйте чотирикутний полігон.

Це може бути будь-якого розміру, нерегулярної форми, конденсату, конвексу тощо. Головне, що має чотири кути і прямі сторони.





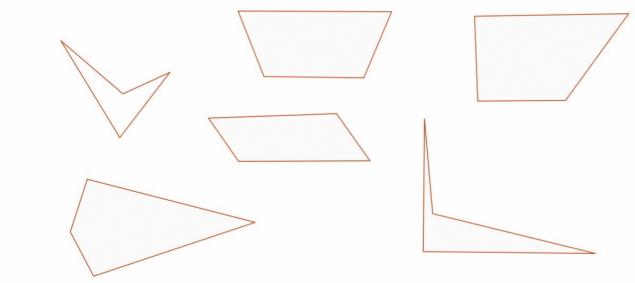
Вказуйте середину з кожного боку полігону.

Підключіть центральні точки до одного. Кожного разу ви отримаєте ідеальний паралелограм.







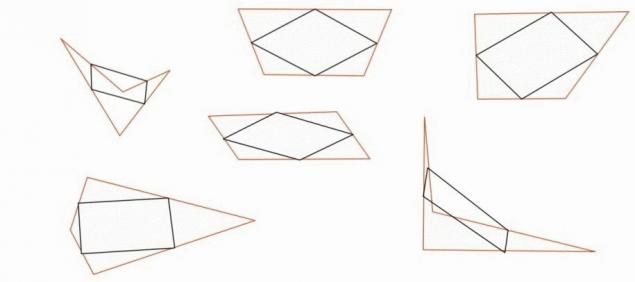
Джерело: Mixstuff.ru

Джерело: /users/1077