Парадоксальные de matemáticas, una decisión que contradice el sentido común

 

En matemáticas hay un montón de ejemplos de situaciones que pueden existir en la realidad, pero no tienen una explicación lógica, y, por lo tanto, nos pone en el callejón sin salida completo.

Los siguientes problemas relacionados con la teoría de la probabilidad, no dejará que te aburras y que ayudará a probar sus capacidades mentales:

1. El problema de monty ХоллаПредставьте que usted está participando en el espectáculo, donde el presentador le muestra tres puertas. Por una de las puertas se encuentra el premio – el coche nuevo, y a los dos restantes – dos de la cabra. Usted puede elegir cualquiera de la puerta y obtener el premio, que detrás de ella se esconde.

Usted elige la puerta y, a continuación, el presentador abre una de las otras dos puertas (líder sabe donde se esconde la máquina, pero siempre abre la puerta, detrás de la cual está el macho cabrío).





 

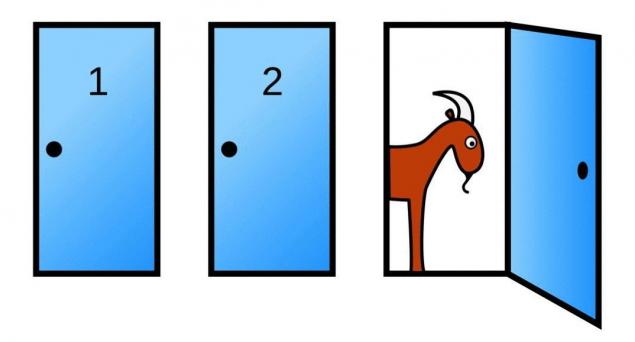
El presentador le pregunta:

– Si desea cambiar su elección?

– O permanezca en el mismo de la puerta, que eligió?

Su decisión?

Por lo tanto, usted decide dejar la versión anterior de la elección.

• Ya que no hay ninguna diferencia, cambiar de puerta o no.
  
  
• Ya sólo quedan dos puertas, la oportunidad de adivinar dónde se encuentra la máquina, es de 50/50.
  
  
• Es cierto?
  
  

Es INCORRECTO!





Respuesta correcta: siempre se deben cambiar su selección, ya que entonces la probabilidad de ganar el coche será dos veces más.

• El jugador, cuya estrategia consistía en el hecho de que cada vez que cambiar seleccionada la puerta, reproduce sólo en el caso de que él originalmente elige la puerta, por la que se encuentra el vehículo.
  
  
• Puesto que la probabilidad de elegir el vehículo en el primer intento es de uno a tres (33%), la posibilidad de no elegir un coche, si un jugador va a cambiar su selección, también es de uno a tres (33%).
  
  
• Esto significa que el jugador, que ha utilizado la estrategia de cambiar de puerta, gana con una probabilidad del 66 % o de dos a tres.
  
  
• Esto duplica las probabilidades de ganar del jugador, cuya estrategia – cada vez que de no cambiar su elección.
  
  

Todavía no crees? Supongamos que usted ha elegido la puerta nº 1. Aquí se presentan todas las opciones posibles de lo que puede ocurrir en este caso:





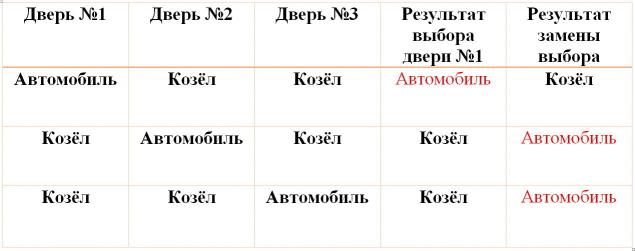
Si usted deja su elección inicial, usted puede ganar una vez de tres; si cambia de elección es la persona que adivina dos veces de tres.

Usted todavía no está seguro? Vamos hagamos lo mismo, con sólo 50 de las puertas. Usted elige la puerta nº 1.





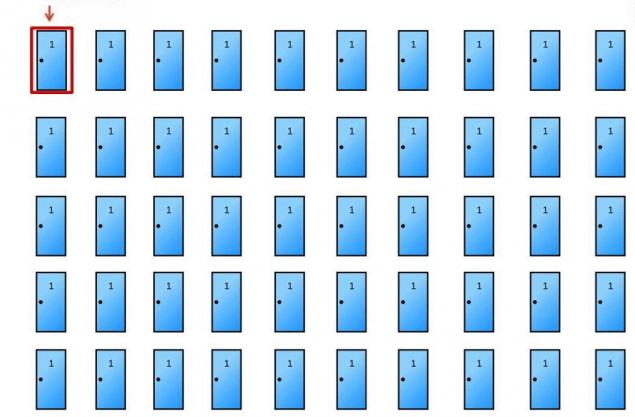
Y abrimos el resto de 48 puertas detrás de las cuales se ocultan de las cabras. Usted está seguro en su elección? Recuerda que tienes 1 oportunidad de 50 adivinar la puerta con el primer intento. Aquí funciona el mismo principio.





Por supuesto, el juego implica que seguramente querían ganar un coche, y no el de la cabra.

2. La paradoja días рожденияПредположим, usted trabaja en una oficina donde trabajan los 23 trabajadores, incluido usted. ¿Cuál es la probabilidad de que dos de los empleados en la oficina coinciden cumpleaños?

(No tomamos en cuenta el 29 de febrero)

Su equipo de 23 de personal (está bajo el nº 14):





Respuesta: la probabilidad de que dos personas en la oficina de cumpleaños cae en el mismo día, es del 50%.

• Si el número de personas alcanza la cifra de 366, estadísticamente se garantiza que al menos dos personas de cumpleaños coinciden, porque es posible que sólo 365 días probables de nacimiento.
  
  
• Sin embargo, si tomamos en cuenta que todos los cumpleaños pueden ser iguales, para un grupo de 57 personas, la probabilidad de tal coincidencia será del 99%.
  
  

¿Cómo podemos averiguar?

• Volvamos a 23 compañeros de la oficina, para entender cómo esto es posible.
  
  
• Formulamos lo contrario: no el de dos personas en el grupo coinciden cumpleaños.
  
  
• Averiguar la probabilidad de que al menos dos personas en la oficina справляют cumpleaños en un día, es muy difícil, si directamente encontrarse con esto.
  
  
• Averiguar la probabilidad de que ninguno en el grupo no coinciden cumpleaños, es mucho más fácil.
  
  

La probabilidad de que dos personas no coinciden cumpleaños, es la siguiente:





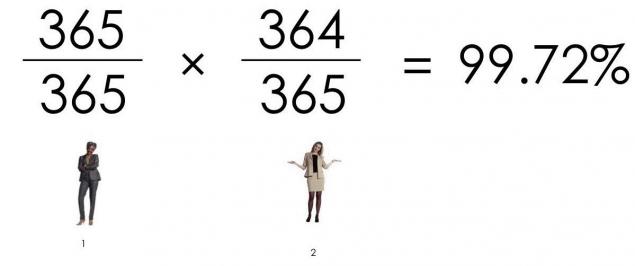
La probabilidad de que tres personas no coinciden cumpleaños, es la siguiente:





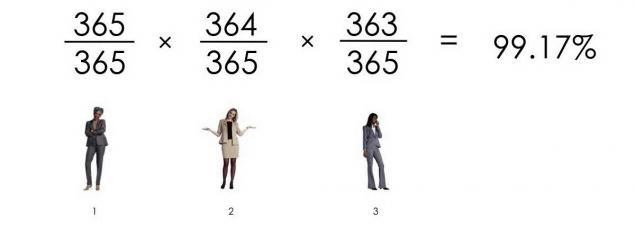
La probabilidad de que cuatro personas no coinciden cumpleaños, es la siguiente:





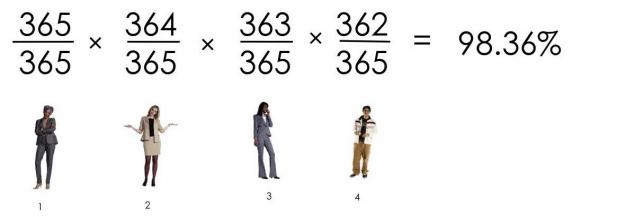
Ve, a qué conclusión llegamos? La probabilidad de que el 23 de personas de cumpleaños no coinciden, es la siguiente:





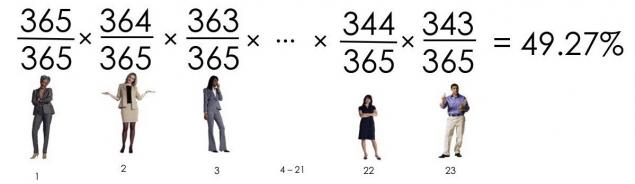
Así como la posibilidad de que nadie nació en un día, es de 49,3%, la probabilidad de que al menos dos personas de cumpleaños coinciden, es decir, el 50,7%.

Así es como se ve la curva de la probabilidad:



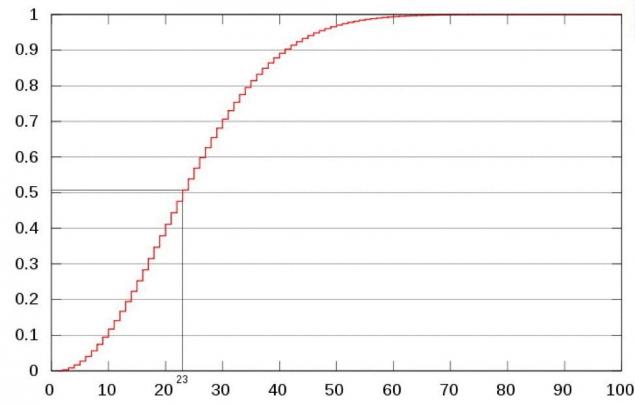
Vertical: la probabilidad de vapor; horizontal: número de personas

3. Tus amigos es mucho más popular que usted o la "paradoja de la amistad"por ejemplo, en el lenguaje de la соцсетей, las personas a las que sigue el usuario, y aquellos que lo sigue, poseen una gran cantidad de фолловеров que él mismo.

• Este fenómeno se basa en la idea de que la mayoría de la gente de amigos menor que el de sus amigos.
  
  
• En 1991, el sociólogo scott Фельд hizo un descubrimiento sorprendente. Se encontró que el 74% de las personas de los amigos menos que sus amigos tienen, en promedio.
  
  

Veamos esta afirmación con un ejemplo. Antes de usted de nuevo muestra la oficina en la que trabajan 20 personas (por ejemplo, suponga que los otros tres fue despedido). Las líneas de la figura señaló que con nadie en la oficina tiene amistad.

El calendario de las relaciones de amistad:





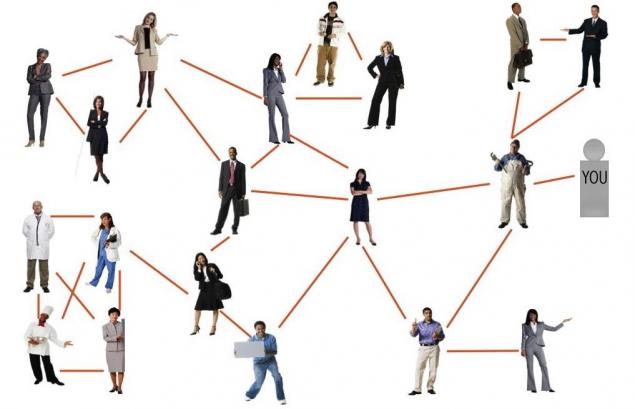
En este colectivo, en promedio, el empleado tiene 2,85 amigos. Sin embargo, el promedio de la cantidad de amigos con los que jugar muy bien los amigos de este hombre, es de 3,39.

Estas personas fueron quienes tiene un promedio de número de amigos, como se muestra arriba. Por lo tanto, ellos son los más populares miembros de la colectividad. Pero lo más importante es que el 17 de 20 personas en la oficina son amigos, por lo menos, uno de estos hombres:





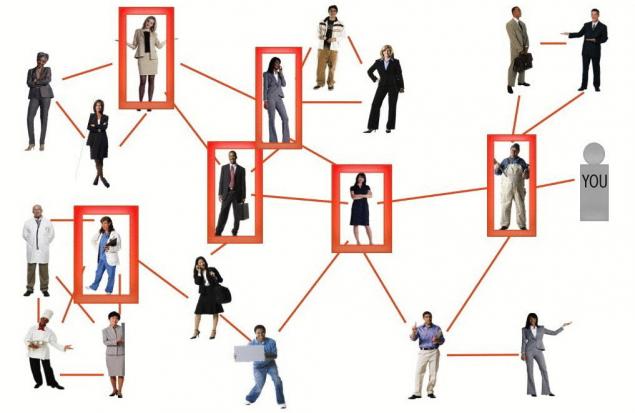
Esto es sólo un ejemplo, pero en la vida real se encuentra la confirmación.

• En twitter los usuarios que sigues, con mayores probabilidades de tener un mayor número de suscriptores, lo que usted mismo. La misma situación con tus amigos en facebook o Twitter.
  
  
• De hecho, usted tiene más probabilidades de tener amistad con alguien, ¿quién es el propietario de un gran número de amigos, que con lo que tiene amistad con el pequeño número de personas.
  
  
• Esta paradoja también se aplica a las relaciones sexuales.
  
  
• Si una persona promedio es en las relaciones sexuales con otras cuatro personas y otro con una "ilegible" de la pareja, sus parejas sexuales serán, en promedio, tener más parejas sexuales que en realidad, de una persona que practica erráticos relaciones sexuales.
  
  

4. La tarea de los tres узниковЭтот la paradoja publicó por primera vez el matemático martin gardner en la columna "juegos Matemáticos" en la revista Scientific American en el año 1959.

Tres detenidos, A, b y c se sientan en celdas de aislamiento y condenados a la pena de muerte. El gobernador elige aleatoriamente uno de ellos y se compadece de él. El guardia, guardia de detenidos, sabe quién es perdonada, pero no tiene el derecho de decir esto.

• Siendo el más valiente, el recluso Y pide a los guardianes de nombrar su nombre (En o C) de un preso, el que será ejecutado.
  
  
• El recluso Y propone: "Si En misericordia, dime que será ejecutado C. Si la misericordia De, di, que será ejecutado Siglo, Si yo fui recibido a misericordia, yo, подбрось una moneda y llama a cualquier nombre".
  
  
• El guardia responde a un preso Y que el ejecutado se recluso S.
  
  

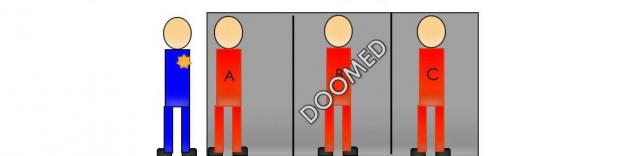
• El recluso Y emocionado, ya que ahora la probabilidad de supervivencia es de 1 / 2, 1 / 3, de modo que uno de los detenidos, b o c, será indultado.
  
  
• El recluso Y en secreto le dice a un preso Con el que será ejecutado. El detenido también emocionado, ya que todavía cree que la probabilidad de supervivencia de un preso Y es de 1 / 3, y la probabilidad de supervivencia ha aumentado a 2 / 3.
  
  

Quién se equivoca?

Respuesta: de los Derechos del recluso S.

1) Inicialmente, todos los tres, el preso tienen una oportunidad de ser de tres помилованными. El guardia dijo que el preso En ser ejecutado, lo que significa que los acontecimientos se desarrollan en uno de dos escenarios:

– Será indultado (1 posibilidad de 3)

– Y se misericordia y la moneda muestra "A" (1 posibilidad de 6)

2) Esto significa: la posibilidad de que el detenido Y será perdonada, constituyen la mitad de probabilidades de que se ha concedido el indulto. Y el recluso no hay posibilidades de ser помилованным.

3) por lo tanto, la probabilidad de ser помилованным sigue siendo неименной – 1/3, mientras que la probabilidad De ser помилованным aumenta hasta 2/3 de su capacidad.

Si usted todavía tiene dudas, echa un vistazo a la lista completa de las posibilidades de cada recluso:





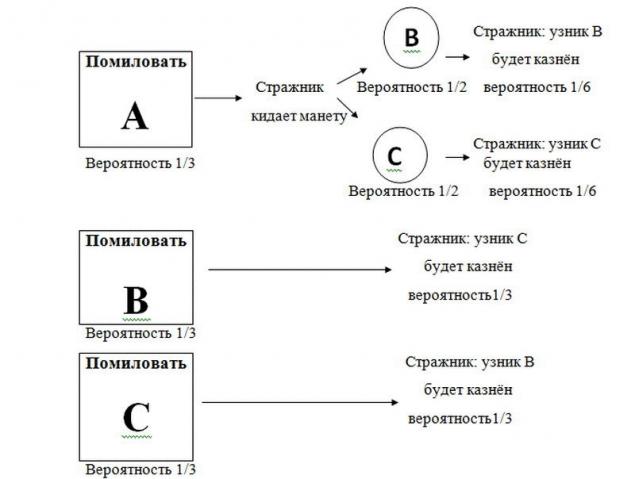
Y si echa un vistazo por ejemplo, donde el guardia informa de que el preso En ser ejecutado, veremos que el preso Con el que tiene dos veces más probabilidades de ser помилованным que el preso A:





Ya que sabemos con certeza que tiene El 0% de posibilidades de ser помилованным, y que tiene dos veces más probabilidades de ser помилованными que Y, entonces:

El guardia informa que será ejecutado





 

5. La perfecta articulación de cuatripartito многоугольникаНарисуйте cuatripartito polígono.

Puede ser de cualquier tamaño, de forma irregular, cóncavo, convexo, etc. lo Importante, para que tenga las cuatro esquinas y directa de las partes.





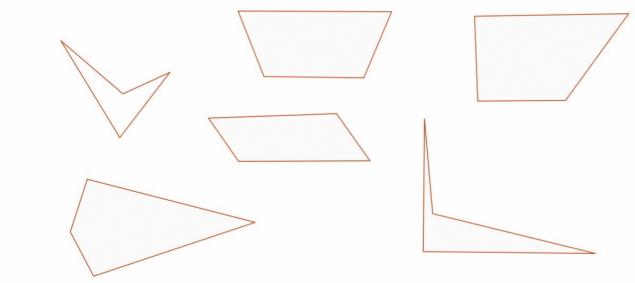
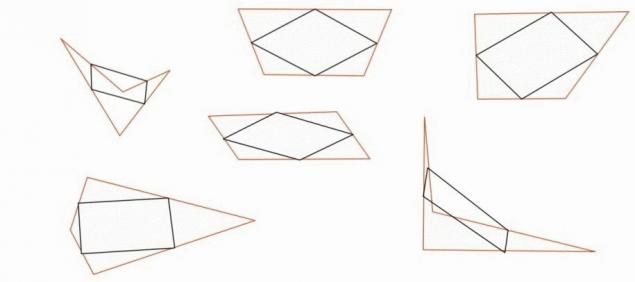
Marque el punto medio de cada lado del polígono.

Conecte los puntos centrales entre sí. Cada vez que usted salga perfecta articulación.





 

fuente: mixstuff.ru

Fuente: /users/1077